
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Механика и экономика. Некоторые замечания.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Как известно, методы механики применимы к системам, в которых на фоне изменяющейся ситуации минимизируется или максимизируется некоторая функция (например, энергия или энтропия). Как было замечено, «единство природы выражается в удивительной похожести дифференциальных уравнений, описывающих совершенно разные по своей природе процессы». Существуют примеры аналогии между механическими, термодинамическими и экономическими объектами. Особое значение «метод аналогий» имеет при математическом моделировании трудноформализуемых объектов. К таким объектам относятся и экономические системы. Следует подчеркнуть, что математические модели трудноформализуемых объектов содержат в себе плохо или не полностью известные поведенческие характеристики живых существ. Поэтому к ним нельзя предъявлять требования адекватности и точности, характерные для моделирования проблем техники. Однако и в этой сфере анализа прогноз и принятие решений в немалой мере основаны на использовании каких-то моделей и методов моделирования (пусть часто и примитивных). Механико-экономические аналогии имеют место не только для общих формулировок проблем, но и для многих содержательных конкретных понятий (сила - предельная прибыль, реакция связей - предельные издержки и т.д.). Одна из возможных механико-экономических аналогий - аналогия между равновесием материальной частицы в потенциальном поле внешних сил и выбором оптимального плана производства. Небольшой иллюстративный пример [8.1]. Многие технические конструкции (системы) могут быть описаны с помощью потенциальной функции, минимальное значение которой определяет локальное устойчивое состояние конструкции. Само состояние описывается положением точки в некотором пространстве состояний конструкции. Вводиться понятие потенциала. Потенциал Р - (от латинского слова potentia - сила) это возможности, средства, запасы, которые могут быть приведены в действие, использованы для решения какой-либо задачи, достижения определенной цели. С физической точки зрения - это понятие, характеризующее широкий класс силовых полей (электрических, гравитационных и т.п.) и вообще поля физических величин, представляемых векто-рами (поля скоростей и т.п.). Пусть единичная масса (точка на рисунке 116) находиться в поле силы тяжести и может занимать любое положение в пространстве, ограниченном снизу твердой поверхностью, уравнение которой y`(х) где х, у - координаты частицы. Расстояние частицы от оси у у Рис. 116 Поле силы тяжести потенциально, т.е. существует функция (потенциал) Р(х, у), такая, что компоненты ее градиента определяют внешнюю силу, действующую на материальную частицу. Следовательно, потенциал дается формулой P=-qy, в которой опущена несущественная аддитивная постоянная. Изменение потенциала при перемещении частицы в поле силы тяжести равно работе А, совершаемой этой силой и определяется начальным и конечным положениями частицы (только координатой у) А= Точка х*, у* называется ПОЛОЖЕНИЕМ РАВНОВЕСИЯ, если частица помещается в нее и, имея нулевую скорость, остается в ней любое время (при наложенных связях и внешней силе). Потенциал в точке равновесия достигает экстремального значения. На рисунке равновесными являются точки минимума функции у'(х) (в них сила тяжести уравновешивается реакцией опоры). Любое возможное, не противоречащее связям, малое перемещение частицы из этих точек приводит к тому, что над нею будет совершена работа, и потенциал уменьшиться. Итак, поиск устойчивого положения равновесия сводиться к решению задачи Р(х, у) ->тах при у≥ у'(х), 0≤х≤х' (*) Этот закон покоя (закон Мопертюи) аналогичным образом формулируется и для более общих механических систем. Если, например, на частицу действуют, кроме силы тяжести, другие потенциальные силы, то точки равновесия не обязаны совпадать с точками минимума функции у'(х). В экономической интерпретации эта задача называется задачей НЕЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ и часто возникает при планировании производства. Пусть предприятие выпускает продукцию (кирпичи), объем которой обозначим х, 0 ≤ х ≤ х`. Для производства предприятию необходимо затратить некоторый ресурс (например, глину), остаток которого после выполнения плана обозначим у (начальный ресурс равен уo исчитается независимым от величины плана х). Известно, что производство происходит при некоторых ресурсных ограничениях сверху, т.е. уo ≤ у ≤ у'(х), 0 ≤ х ≤ х'. у'(х) - минимальное количество неиспользованных ресурсов, которое предприятие по технологическим, финансовым или иным причинам обязано иметь в своем распоряжении после выполнения плана х. В упрощенной постановке прибыль Р(х, у) равна разности между стоимостью продукции F-х и стоимостью затраченных ресурсов q (y-y°): P(x,y) = F·x+(уo – y)q, (**) где F,q - цены единицы продукции и ресурса соответственно (остальные затраты будем считать несущественными). Задача планирования производства состоит в том, чтобы выбрать план х*, выполнение которого дает максимальную прибыль при внутренних ограничениях: Р(х, у)→тах при у°<у, 0 ≤ х ≤ х' (***) Формулировки, подобные (***), справедливы для весьма общих задач планирования. Для получения более полной аналогии можно ввести дополнительно к силе тяжести потенциальную внешнюю силу F, действующую на частицу в направлении оси х. Тогда потенциал будет: P(x,y) = Fx + qy, т.е. почти совпадает с (**). Итак задачи (**) и (***) аналогичны и имеют совпадающие решения х* и у*. На оптимальном плане х*,у* максимального значения достигает не только экономический аналог потенциала - прибыль, но также энтропия. Энтропия - от греческого слова entropia - поворот, превращение. Статистическая физика рассматривает энтропию как меру вероятности пребывания системы в данном состоянии. Неравновесные процессы в изолированной системе сопровождаются ростом энтропии и приближают систему к состоянию равновесия, в котором энтропия максимальна. Для некоторого произвольного неоптимального плана (х,у)≠(х*,у*) рассмотрим окрестность е всех соседних планов (х,у). Т.е. выполнено условие | обладают обоими этими свойствами. Это означает, что в окрестности точки (х,у) можно провести частичное упорядочение планов относительно друг друга, т.к. известна процедура предпочтения одних планов другим. Очевидно, объем «плохих» планов меньше объема е - окрестности: V(х*,у*,ε)<Vε Если ε - окрестность оптимального плана (х*,у*), то все планы этой области менее предпочтительны по отношению к (х*,у*). В этом случае объем «плохих» планов равен объему всей s - окрестности: Можно ввести функцию E(x,y,s) = которая служит мерой упорядоченности данной системы. Чем «ближе» точка х, у к оптимальному состоянию (х*,у*), тем больше значение функции Е. Очевидно, что Е< 1при всех (х, у) ≠ (х*,у*} и достигает своего максимума Е = 1в точке (х*,у*). Она и является экономическим аналогом энтропии в рассматриваемой задаче. Также как и механические аналоги, термодинамические аналогии справедливы для многих весьма общих экономических систем и применяются при их исследовании. С этих позиций можно рассмотреть организацию рекламной кампании, взаимозачет долгов предприятий, макромодель экономического роста, некоторые модели соперничества (отношения в системе «хищник-жертва», гонка вооружений, динамика распределения власти в иерархии, правовая система «власть - общество» (стационарные распределения и выход власти за рамки полномочий), процессы в переходной экономике и др.). Математические модели экономики разрабатываются давно, и процесс этот активно продолжается и поныне. Еще несколько замечаний. Прежде всего, момент, на который еще раз хотелось бы обратить внимание. Это определенная опасность оперирования усредненными величинами. В ряде случаев использование осредненных значений не позволяет сделать надежное заключение. Они вуалируют ситуацию, пряча возможные опасности. Как мы уже знаем, особенно четко это было видно при рассмотрении явления ползучести материалов. Опора на средние величины может привести к неверным оценкам надежности конструкции. To же имеет место и в экономике. Средние величины и здесь могут увести от существа дела. Как в известном анекдоте о положении дел в больнице. Средняя температура по всем больным 36,6°, но половина из них имеет 30° (т.е. они свели счеты с нашим бренным миром и остывают), другая половина больных с температурой 43° безнадежна. Так же может обстоять дело и, например, со средней зарплатой. Примером решения экономических задач методами механики может оказаться возможность построить аналогию «ползучесть материалов-зарплата», рассматривая зарплату сотрудников предприятия(организации),как аналог суммарной деформации ползучести (или скорости ее нарастания). Как «средняя» кривая нарастания деформации ползучести не может гарантировать надежную работу конструкции, так и осредненная по организации зарплата еще ничего не говорит о ее устойчивой производительной работе. Если в каких-то элементах предприятия (структурных подразделениях) зарплата будет существенно отличаться от «среднего» значения, то ситуация в организации может выйти из состояния «рабочего» равновесия и система окажется неработоспособной, быстро приближаясь к «катастрофе». Кстати можно отметить, что многие аналитики считают, что среди причин снижения роста производительности труда (а, как известно, производительность есть главный показатель экономического благополучия), не последними являются чрезмерное число управляющих и слишком высокие оклады руководителей. Таким образом, как и в ползучести, существенным моментом, подлежащим тщательному изучению, является определение допустимой ширины полосы разброса по зарплате. Конечно, построение надежной полосы разброса с хорошей доверительной вероятностью потребует обстоятельного достоверного статистического анализа деятельности разных, как внутриотраслевых, так и внеотраслевых, предприятий. Приводимая аналогия с разбросом данных по ползучести материалов носит чисто формальный характер, природа явлений разная. Но, тем не менее, подходы к анализу разброса данных в конкретных ситуациях подобны и могут позволить вскрыть действительное положение дел. И еще. Нельзя в экспериментах лабораторных или мысленных исчерпать многообразие работы элементов конструкций или систем. Нужна теория, позволяющая из простых экспериментов предсказать, хотя бы в первом приближении, поведение системы, подвергнутой иному, чем в условиях опыта, воздействию. Для этого, как неоднократно подчеркивалось, удобно построить модель. Конечно, не всегда процессы, сущность которых мы, как следует, еще не знаем, можно моделировать, с надеждой на успех, механическими схемами. Но моделирование удобно уже тем, что даже в случаях, когда по лучение количественных результатов затруднено, мы имеем возможность получить суждение о качественной стороне процесса и о влиянии на него различных параметров. Таким образом, естественно приходим к мысли функционального моделирования. Моделирование - это форма предварительного истолкования явления. Сейчас наряду с субстратно-атрибутивным приобретает все большую роль функциональное описание не в терминах внутренних причинных зависимостей, а в терминах внешних функциональных связей управления. Хотя при таком подходе внутренние механизмы процесса могут оказаться еще скрытыми от нас, тем не менее мы можем получить вполне надежную картину внешних функциональных связей системы и среды. А, как известно, именно функциональные связи системы и среды весьма важны для процессов управления. Такой подход позволяет описывать системы, весьма далекие по внутреннему субстрату, с помощью обобщенной модели двухмерного вектора, одна составляющая которого характеризуется параметрами «входа» системы, а вторая параметрами «выхода» "Выход" = F("Вход") Основой такого подхода являются: - во-первых, признание объективности, независимости от сознания субъекта, внешних функциональных связей; - во-вторых, что внутренние причинные механизмы, которые сегодня нам еще могут быть неизвестны и от которых мы сегодня вынуждены относительно отвлекаться, существуют объективно и будут познаны завтра. Типичной экономической моделью является формирование бюджета предприятия, организации, страны. Базовую основу модели должны делать управленцы - инженеры, обладающие большими знаниями, эрудициeй иглубоким перспективным мышлением. Экономическое обеспечение модели должны затем сделать экономисты. Но если бюджет нормируют"чистые"экономисты, руководствующиеся только "бухгалтерскими" навыками, то модель может оказаться не работоспособной. В заключение еще несколько слов о механико-экономическом аспекте. Организация управления (иерархия) не может использоваться без учета многих ее потенциальных недостатков, одним из которых является растущая тенденция увеличения некомпетенции руководства в таких системах (принцип Питера) и др. Управленческая лестница должна быть короткой. Большинство промежуточных ступеней к производственной деятельности (предприятия) отношения не имеют, они живут в собственном «замкнутом подмире» (подсистеме) и обслуживают самих себя, создавая внутренние напряжения в работе организации, так же как и «избыточные» связи в статически неопределимых механических системах. Любой элемент конструкции, отличающийся от окружающих его элементов своими «жесткостными» свойствами, вызывает концентрацию напряжений и может быть опасен. Также следует иметь в виду, что при математическом моделировании трудноформализуемых объектов «теоретики слишком часто бывают увлечены элегантностью своих методов и не заботятся в достаточной мере о соответствии исходных предположений действительности, получая в результате правильные ответы нереальных задач». И еще несколько слов о некорректности задач экономики. Некорректно поставленные задачи близко примыкают к теории катастроф [8.2]. Как отмечал А.Н. Тихонов [8.3], «среди математических задач выделяется класс задач, решения которых неустойчивы к малым изменениям исходных данных. Они характеризуются тем, что сколь угодно малые изменения исходных данных могут приводить к произвольно большим изменениями решений. Задачи подобного типа, по существу, являются плохо поставленными». Они принадлежат к классу некорректно поставленных задач. Если исходные данные известны приблизительно (во многих экономических задачах они задаются с мало достоверной вероятностью), то упомянутая неустойчивость приводит к практической неединственности решения в рамках заданной точности и к большим трудностям в выяснении смысла получаемого приближения. К числу важных задач этой категории относятся задачи создания систем автоматической математической обработки результатов экспериментов (включая интерпретацию), задачи оптимального проектирования систем. Исходные данные некорректно поставленных задач обычно содержат и случайные погрешности. Поэтому при построении решений (приближенных решений) и при оценке их погрешности, в зависимости от характера исходной информации, возможен как детерминированный подход, так и вероятностный. Пусть z1 - количество выпускаемых изделий i -го наименования, 1 <i<n, а 1- максимально возможное число изделий i -го наименования, C 1 - суммарная трудоемкость для i -го изделия по всем основным группам оборудования (по всем технологическим переходам). Тогда скалярное произведение Y 1 (z) = (C, z) векторов С = {С 1 ,С2,...,Сn} и z = {z 1 ,z2,...,zn} характеризует загрузку оборудования при плане z выпуска изделий. Пусть b 1- фонды времени j-й группы оборудования, 1≤ j ≤т, аij - трудоемкость для i- гo изделия на j-й группе оборудования. Обозначим через G множество векторов z (планов), удовлетворяющих условиям: b - A(z)≥0, 0≤ z≤ a, где а и b - векторы b - {b1,b2,..., bп}, а = {а1, а2,..., ап}, А = { аij } - матрица с элементами аij Задача определения оптимального плана maxz Функцию Y(z) называют ЦЕЛЕВОЙ ФУНКЦИЕЙ задачи. По данным одного из предприятий были рассмотрены с разной точностью оптимальные квартальные планы, отвечающие некоторому набору исходных данных. Расчеты показали, что для сравнительно близких оптимальных значений целевой функции Y(z) (при отклонениях порядка 1 %) количество изделий, подлежащих выпуску по этим оптимальным планам, по отдельным наименованиям колеблется в пределах нескольких сотен. Т.о., задача является неустойчивой. Итак, исходные данные в задачах оптимального планирования задаются обычно приближенно. Если терминологически различить РЕШАЕМУЮ (точную) и ЗАДАВАЕМУЮ (заданную, приближенную к точной), то задаваемая задача не позволяет сделать заключения ни об устойчивости решаемой задачи, ни о единственности ее решения. Точное же решение заданной задачи неэффективно для исследования решаемой задачи. Обычно в математической постановке задач оптимального планирования при выборе целевой функции Y(z) = (C,z) учитываются не все факторы. К ним относятся, например, требования небольшого отклонения искомого оптимального плана, отвечающего новым (мало отличающимся от прежних) исходным данным, от прежнего плана (требование минимизации организационной перестройки). Введение в новой целевой функции слагаемого В заключение раздела, обратим внимание на математическую теорию катастроф, которая с успехом может бить использована в подобных случаях. Как уже неоднократно отмечалось, все задачи механики (и экономики также) решаются составлением уравнений равновесия. И катастрофа (разрушение конструкции, экономическим спад и пр.,) наступает тогда, когда система вынуждена искать новое состояние равновесия. И, таким образом, катастроф нужно рассматривать, как переход системы в новое состояние равновесия. Как искать причины катастрофы? Мы уже обращали внимание на то, что, рассматривая какие-либо процессы и питаясь их описать, мы из сложного явления выделяем ту задачу, которая интересует нас в настоящее время, спуская, в то же время, многие побочные процессы, считая их не существенными для нашей задачи. То есть работаем по схеме (кстати, так развиваются все науки); побочные реакции системы, которые вследствие их кажущейся малости не рассматриваются. Часто их проcто не замечают. Но эти, казалось бы, не очень существенные малозаметные реакции системы, накапливаясь, могут привести к катастрофе.
Прогнозирование экономического развития. Составление прогнозных планов, конечно, необходимо. Однако, нужно иметь в виду, что учесть все "риски" и особенности ситуаций, возникающих в развитии экономики страны, фирмы, предприятия, с достаточной достоверностью, в большинстве случаев, не представляется возможным. Наглядность зависимости надежности прогнозов от времени, на которое делается прогноз, может дать график рисунка
КУРСОВОЕ ПРОЕКТИРОВАНИЕ 9.1. Курсовое проектирование и его роль в подготовке инженера. Каждый молодой инженер должен иметь не только хорошую мировоззренческую подготовку и достаточный комплекс знаний, не только некоторый опыт производственной работы, но и определенные навыки в проведении творческой работы, в умении включать в работу свой творческий потенциал. Последнее может быть достигнуто путем включения будущих инженеров в творческую работу еще на студенческой скамье. Самостоятельная расчетно-конструкторская работа студента весьма эффективно формирует навыки к постоянной самостоятельной деятельности. Успешная деятельность инженера не может базироваться только на знании отдельных сторон инженерного дела. Без знания особенностей изготовления и эксплуатации машин нельзя рассчитывать на успешную работу по их проектированию, а без знаний особенности проектирования и изготовления невозможно надеяться на полное и правильное их использование. Вот почему от каждого инженера, вне зависимости от содержания и характера его работы по специальности, требуются прочные и глубокие знания по проектированию, изготовлению и эксплуатации инженерных сооружений и машин, относящихся к той области техники, в которой он занят, которой он себя посветил. Сказанное объясняет обязательное включение в программы подготовки инженера любой специальности учебного проектирования, каким, в частности, является курсовое проектирование по деталям машин и механическим передачам общего назначения. Курсовое проектирование по деталям машин и механическим передачам общего назначения является первым проектированием студента высшей школы. Значение этого проектирования трудно переоценить. От реального проектирования, выполняемого в проектных организациях, оно отличается немногими этапами: оно не содержит обязательного для реального проектирования составления исполнителями проекта технического задания на проектирование, в котором задаются основные характеристики и требования к будущей машине, и не включает проведения специальных лабораторных исследований, доводки и сдаточных испытаний опытных узлов и пробного образца спроектированной машины. Это, однако, не умаляет роли курсового проектирования во всем комплексе подготовки молодого инженера. Оно является большим и важным звеном этого комплекса и требует от студента некоторой подготовки по таким дисциплинам, как машиностроительное черчение, технология материалов, металловедение, теоретическая механика, сопротивление материалов (механика деформируемого тела), механика машин, технические измерения и основы взаимозаменяемости, детали машин и механические передачи, технология машиностроения. Знание студентом этих дисциплин не должно носить формального характера. Оно должно опираться на владение навыками самостоятельной работы и на умение выполненному решению рядовой инженерной задачи дать критическую оценку, развернутый и строгий анализ. Лишь при соблюдении этого условия можно рассчитывать на то, что курсовой проект будет выполнен студентом на надлежащем уровне и что из работы над проектом студент извлечет важные для будущего инженера знания, опыт, кругозор.
|
||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 419; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.250.19 (0.015 с.) |

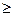 0,
0, х
х 
 = P(y2)-(y1).
= P(y2)-(y1).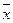 -х|< ε, |
-х|< ε, |  |< ε. Поскольку план (х,у) не оптимален, то в его ε -окрестности всегда существует непустое множество планов, которые: либо не удовлетворяют ресурсным ограничениям (область А и В), либо не имеют преимущества по прибыли в сравнении с планом (х, у) (область С), либо
|< ε. Поскольку план (х,у) не оптимален, то в его ε -окрестности всегда существует непустое множество планов, которые: либо не удовлетворяют ресурсным ограничениям (область А и В), либо не имеют преимущества по прибыли в сравнении с планом (х, у) (область С), либо
 может состоять в нахождении такого вектора
может состоять в нахождении такого вектора  GY1(z)=Y1(
GY1(z)=Y1( можно рассматривать как поправку на влияние неучтенных факторов, а Л - как величину экспертной оценки их влияния.
можно рассматривать как поправку на влияние неучтенных факторов, а Л - как величину экспертной оценки их влияния.




