
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нормальные диаметры валов (по ГОСТу 6270)Содержание книги
Поиск на нашем сайте
9.8. Домашние задания. Задача № 1.

Задача № 2. Подмости для ремонта зданий устроены на горизонтальных бревнахAB, протянутых сквозь оконные отверстия. В сечении С бревно AB передает давление на подоконник. Какого диаметра d следует взять бревна AB, если на участке ВС может лежать нагрузка q=4000 Н/м,
Задача № 3. Определить вес балки AB, если известны силы натяжения веревок F1=120Н и F2=80Н. Заданы углы α=45º и β=30º между вертикалью и веревками АС и ВС соответственно. (154)
Задача № 4. Подобрать размеры прямоугольного поперечного сечения сосновой поперечины пролетом
Задача № 5. При сборке конструкции из 3-х стальных стержней средний оказался на δ=2 мм короче требуемой длины. Чтобы соединить концы стержней в узле В, образовавшийся зазор пришлось устранить за счет натяжения среднего стержня. Определить напряжения, возникшие в стержнях, если площади их поперечных сечений одинаковы. φ=300,

Задача № 6. Определить количество «Z» стальных проволок диаметром d=1,4 мм, из которых должен быть свит канат АВ для подъёма стрелы башенного крана. Грузоподъемность F=3 тонны. Вылет стрелы α=20 м. Высота оголовка Н=3,5 м. Предел прочности проволок при растяжении 1700 Н/мм2. Коэффициент запаса n= 5.
Задача № 7. Деревянная балка длиной
Задача № 8. Определить момент силы относительно начала координат, если сила задана проекциями Fх=Fу=210 Н и известны координаты точки приложения силы х=у=0,1 м. (0) Задача № 9. Деревянная балка квадратного сечения (см. чертеж) защемлена одним концом и нагружена силами Р1=8000 Н и Р2=9000 Н. Определить размеры сторон квадрата, если Ответ: а=18 см (по расчету 17,5 см). Отверстие не опасно, т.к. в сечении через отверстие напряжение всего
Задача № 10. Подобрать сечение нижнего пояса сварной стропильной фермы промышленного здания. Высота на опорах h=2,1 м, в середине пролёта Н=3,3м. Нагрузка приложена в узлах в виде сосредоточенных сил F=7,5 тонн. Материал фермы сталь СтЗ с допускаемым напряжением 160
Вариант 2: h=2,5 м, Н=4 м, F=10 тонн. Задача № 11. Автомобиль двигается со скоростью v1=3,6 км/ч, а монтажная вышка поднимается со скоростью v2=0,5 м/с. Определить абсолютную скорость рабочего, который стоит на вышке неподвижно. (1,12)
Задача № 12. Определить длину
Задача № 13. Балка таврового сечения (см. чертеж) (размеры длины в сантиметрах) изгибается в плоскости ОО нагрузкой, действующей сверху вниз. Какой должна быть высота сечения h, если желательно, чтобы наибольшие сжимающие напряжения вдвое превосходили наибольшие растягивающие напряжения. Ответ: h=4 или 12 см.
Задача № 14. Определить усилия в стержнях, предположив, что средний стержень выполнен из стали, а крайние из алюминия. Модуль упругости стали в 3 раза больше модуля упругости алюминия. Ест=3Еал.
Задача № 15.
Задача № 16. Сечение балки длиной
Задача № 17. Железобетонная плита перекрытия горячего цеха длиной
Задача № 18.
Задача № 19. Деревянная плотина состоит из ряда вертикальных столбов квадратного сечения, обшитых досками (см. чертеж). Какого размера должно быть поперечное сечение столбов и толщина досок, если глубина воды h=2 м, расстояние между осями столбов d=1 м и если допускаемое напряжение на изгиб для дерева 40 Н/мм2? (При расчете досок считать свободно лежащими на двух опорах, а расстояние между опорами принять равным 1 м). Ответ: сторона столба а≈34 см; толщина доски b=6 см.
Задача № 20. Подъёмный кран установлен на грузовой автомашине. Вес противовеса «В» равен
Задача № 21.
Водоудержательная плотина состоит из сплошного ряда деревяннных брусьев к квадратного сечения, опертых на верхнем и нижнем концах на прогоны (см. чертеж). Как велики будут наибольшие нормальные напряжения в этих брусьях от давления поды, если высота брусьев h= 6 м и а = 30 м? Указание. Каждый из брусьев можно рассматривать как балку, свободно положенную на опоры с треугольной нагрузкой (см. чертеж). Ответ: σmах Задача № 22.
Задача № 23. Механизм пресса
Рассчитать зубчатую передачу Zn-Z5.
Задача № 24.
Рассчитать зубчатую передачу Z1-Z2-Z3.
Рассчитать зубчатую передачу Z5-Z6.
СПИСОК ЛИТЕРАТУРЫ
К главе 1 1. Бать М.И., Джанелидзе Г.Ю., Кельзон А.С. Теоретическая механика в примерах и задачах. М., 1965. 2. Тарг С.М. Краткий курс теоретической механики. М., 1986. 3. Граве Д.А.. Теоретическая механика на основе техники. М.-Л., 1932. 4. Николаи Е.Л. Теоретическая механика. М., 1958. 5. Мещерский И.В. Сборник задач по теоретической механике. М.,1933 - 1986. 6. Мисюрев М.А.. Методика решения задач по теоретической механике. М., 1962.
К главе 2 1. Тимошенко С.П. Сопротивление материалов. Л.-М. 1933-1965. 2. Феодосьев В.И. Сопротивление материалов. М., 1979. 3. Ильюшин А.А., Ленский В.С. Сопротивление материалов. М., 1959. 4. Гуле Ж. Сопротивление материалов. М., 1985. 5. Улитин Н.С. Сопротивление материалов. М, 1975. 6. Михайлов А.Ы., Михайлов М.Е. Сопротивление материалов в примерах. М., 1971. 7. Иванов Н.И. Сборник задач по сопротивлению материалов. М.1958.
К главе 3 1. Тимошенко С.П. Курс статики сооружений. Л., 1926. 2. Михайлов А.М. Металлические конструкции в примерах. М., 1976.
К главе 4 1. Артоболевский И.И. Теория механизмов и машин, М., 1975. 2. Артоболевский И.И., Эдельнтейн Б.В. Сборник задач по теории механизмов и машин. М.1973, 3. Левитская О.Н., Левитский Н.И. Курс теории механизмов и машин, М., 1985. 4. Юдин В.А., Петрокас А.В. Теория машин и механизмов. 1976. 5. Юдин В.А. Сборник задач и примеров по ТММ. 1963. 6. Попов А.С. Курсовое проектирование по теории механизмов и механике машин. М., 1986, 7. Ковалев Н.А. Прикладная механика. М., 1982. 8. Кореняко А.С. Курсовое проектирование по ТММ. М., 1975. 9. Кожевников С.П. ТММ. М., 1974. 10. Механика промышленных роботов. Т. 1-3., 1988.
К главе 5 1. Ачеркан. Детали машин. Расчет и конструирование. М., 1968. 2. Решетов. Детали машин. М., 1975. 3. Иосилевич А.Б., Строганов Г.Б., Маслов Г.С. Прикладная механика. М., 1989. 4. Кузъмин А.В., Чернин И.М., Козинцов Б.С. Расчеты деталей машин. Справочное пособие. Минск., 1986. 5. Биргер И.А., Шорр Б.Ф., Иосилевич Г.Б. Расчет на прочность деталей машин. Справочник. М., 1979. 6. Дунаев П.Ф. Конструирование узлов и деталей машин. М., 1978. 7. Польгаузен А. Детали машин. Т. 1 и 2.. С.- Петербург, 1903. 8. Справочное руководство по зубчатым передачам и редукторам. Под ред. Н.А. Калашникова и Б.А. Тайц. М., 1946. 9. Дунаев П.Ф., Леликов О.П. Детали машин. Курсовое проектирование. М., 1984. 10. Орлов П.И. Основы конструирования. М. 1977.
К главе 6 1. Диксон Дж. Проектирование систем: изобретательство, анализ, принятие решений. М., 1969. 2. Альтшулер Г.С. Алгоритм изобретения. М., 1973. 3. Хевиленд Р. Инженерная надежность и расчет на долговечность. М.,1966. 4. М.Бунге. Интуиция и наука. М., 1967. 5. Эдвард де Боно. Рождение новой идеи. М., 1976. 6. Варшавский А.Е. и др. Характер и прогноз развития науки и технологий в России. М., 1994. 7. Вузовская наука на международном рынке научно-технической продукции. Тезисы докладов. Барнаул., 1995.
К главе 7 7.1. Тимошенко С.П., Гудьер Дж. Теория упругости. М., 1979. 7.2. Березин И.С., Жидков Н.П. Методы вычислений, М., 1966. 7.3. Демидович Б.П., Марон И.А. Основы вычислительной математики. М.1966. 7.4. Дьяченко В.Ф. Основные понятия вычислительной математики. М., 1977.
К главе 8 8.1. Самарский А.А., Михайлов А.П. Математическое моделирование. М. Физматлит. 2002. 8.2. В.И.Арнольд. Теория катастроф. МГУ. 1990. 8.3. А.Н.Тихонов, В.Я.Арсенин. Методы решения корректных задач. М. Наука. 1979. 8.4. Е.В.Шишкин, А.Г.Чхартишвили. Математические методы и модели в управлении. М. Дело. 2000.
К главе 9 См. литературу к главе 5.
[1] См. приложение I [2] См.приложение 2 [3] См. приложения IV-VI, VIII-XII [4] См. приложение III [5] См. приложение VII [6]Для перевода в мегапаскали /МПа/ значение σ в кг/мм2 нужно умножить на 10
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 353; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.008 с.) |

 =2 м. Допускаемое напряжение при изгибе [σ]=10 Н/мм2.
=2 м. Допускаемое напряжение при изгибе [σ]=10 Н/мм2.





 .
.
 . При эксплуатации этой балки в ней пришлось просверлить насквозь отверстие d=7 см. Не опасно ли это отверстие для прочности балки?
. При эксплуатации этой балки в ней пришлось просверлить насквозь отверстие d=7 см. Не опасно ли это отверстие для прочности балки?
 . Сечение полосы запроектировать из двух неравнобоких уголков.
. Сечение полосы запроектировать из двух неравнобоких уголков.

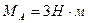 , если интенсивность распределенной нагрузки
, если интенсивность распределенной нагрузки  . (3,0)
. (3,0)



 .
.
 и толщиной
и толщиной  уложена у одной из стен с зазором
уложена у одной из стен с зазором  при температуре
при температуре  . Определить величину горизонтального давления плиты на стену в условиях эксплуатации цеха при температуре
. Определить величину горизонтального давления плиты на стену в условиях эксплуатации цеха при температуре  . Коэф. линейного расширения железобетона
. Коэф. линейного расширения железобетона  .
. 



 т. Вес автомашины с краном без противовеса, равный
т. Вес автомашины с краном без противовеса, равный  т, приложен в точке «С». Определить наименьшее расстояние DE между осями колёс автомашины и наибольший вес поднимаемого груза «А», при наличии которых автомашина не опрокинется как с грузом «А», так и без него. Размеры указаны на рисунке.
т, приложен в точке «С». Определить наименьшее расстояние DE между осями колёс автомашины и наибольший вес поднимаемого груза «А», при наличии которых автомашина не опрокинется как с грузом «А», так и без него. Размеры указаны на рисунке.

 91 кг/см3.
91 кг/см3.






