
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение напряжений при растяжении
Брус нагружен силой F. Нагружение бруса силой F будем считать статическим. Используем метод сечений. Определим напряжение в сечении 1-1, так как оно имеет наименьшую площадь (рис.22).
Рис.22
Внутренние силы будут параллельны оси стержня, так как они должны уравновесить внешнюю силу F. Следовательно, в поперечном сечении (например, 1-1) возникают только нормальные напряжения s. Запишем уравнение равновесия
где s dA – элементарная внутренняя сила на площадке
Перемещения и деформации при растяжении. Изменение первоначальной длины стержня под действием силы F называется удлинением. Линейная деформация определяется как относительное удлинение (величина безразмерная, так называемая мера Коши) (рис. 23).
Рис.23
Закон Гука. Непосредственными опытами установлено, что в пределах упругих деформаций абсолютное удлинение стержня ∆l пропорционально приложенной силе. Тогда следует, что напряжения пропорциональны относительному удлинению (укорочению). Этот закон (Р. Гук, 1576 г.) записывается так
где Е – коэффициент пропорциональности (постоянная для данного конкретного материала), называется модулем упругости при растяжении или сжатии (модуль упругости первого рода). Из формулы видно, что размерность Е будет Н/м2. Закон Гука можно записать в виде
Для упруго-деформированного тела это и есть уравнение состояния. Величина ЕА называется жесткостью стержня при растяжении. Расчетное уравнение. Итак, в поперечном сечении растягиваемого стержня возникают напряжения и стержень получает удлинения. Для надежной работы стержня возникающие напряжения и перемещения не должны превышать какие-то определенные (допускаемые) значения. Поэтому необходимо нормирование этих величин. Нормируя величины напряжений и перемещений получаем расчетные уравнения. Чаще нормируют напряжения, в результате получают расчетные уравнения на прочность
где [ σ ] – допускаемое значение напряжения. Оно зависит от рода материала и характера деформированного состояния. Расчетные уравнения позволяют решать следующие задачи: 1. Так называемую прямую задачу. По заданной силе F и допускаемому напряжению [ σ ] определяются размеры поперечного сечения. 2. Задачи проверочного характера. По заданной силе и известной площади поперечного сечения А определяются фактические напряжения и сравниваются с допустимыми. Или же по известным А и [ σ ] определяют допустимую нагрузку. Температурные напряжения. При изменении температуры статически неопределимой системы в ней возникают напряжения и при отсутствии внешних нагрузок. Если, например, стержень защемлен обоими концами (рис. 24), то при изменении его температуры в нем возникают так называемые температурные напряжения. Величина их определяется соотношением
где α – коэффициент линейного расширения.
Рис. 24
|
|||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 326; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.34.178 (0.005 с.) |


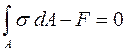 ,
, . Найти отсюда σ невозможно, так как неизвестен закон распределения σ по сечению бруса. Рассмотрим деформацию стержня. Как показали опыты, продольные элементы растянутого стержня удлиняются одинаково. Это дает основание считать, что нормальное напряжение по сечению постоянно. Тогда третий этап определения напряжений дает
. Найти отсюда σ невозможно, так как неизвестен закон распределения σ по сечению бруса. Рассмотрим деформацию стержня. Как показали опыты, продольные элементы растянутого стержня удлиняются одинаково. Это дает основание считать, что нормальное напряжение по сечению постоянно. Тогда третий этап определения напряжений дает и
и  Н/м2.
Н/м2. .
.
 ,
, .
. или
или  ,
,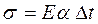 ,
,



