
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основы расчетов на прочность за пределами упругости
2.16.1. Пластичность. Как мы уже знаем, при достижении нагрузкой некоторого значения к упругим деформациям добавляются остаточные (пластические). Эти деформации не исчезают после снятия нагрузки. Для расчетов конструкций, в элементах которых могут быть допущены пластические деформации, используются так называемые теории упруго-пластических деформаций. Отличие пластического деформирования связано с нелинейной зависимостью между напряжением и деформацией. Закон Гука теряет свою силу и прямая пропорциональность между напряжениями и деформациями заменяется более сложной зависимостью, определяемой видом диаграммы растяжения на интересующем нас интервале нагрузок. И хотя пластические деформации существенно больше упругих (имеются в виду, главным образом, машиноподелочные и некоторые строительные материалы), они по-прежнему малы по сравнению с единицей. Конечно, можно ставить вопрос и о расчетах при больших пластических деформациях, не ограничивая их величину. Такие задачи возникают, например, при анализе прессовых и вытяжных технологических операций. Но они носят специальный характер и мы их касаться не будем. Расчеты же в области малых пластических деформаций часто встречаются в инженерной практике при исследовании прочности и жесткости элементов конструкций сложной формы, в небольших объемах которых не удается избежать появления пластических деформаций при действии производственных нагрузок. В связи с малостью пластических деформаций к этому классу задач полностью применим принцип неизменности начальных размеров и при составлении уравнений равновесия можно считать, что пластически деформированная система мало отличается от недеформированной. Что же касается второго основополагающего принципа – принципа независимости действия сил, то в данном случае он оказывается неприемлемым. В связи с возникновением в работающей конструкции пластических деформаций весьма существенным является вопрос общих принципов ведения расчета. При пластических деформациях во многих случаях нельзя пользоваться методом расчета по допускаемым напряжениям. В этом случае о пригодности конструкции судят либо по величине возникающих перемещений, либо по величине предельной или разрушающей нагрузки.
Для аппроксимации опытной кривой растяжения предложено достаточно много зависимостей, например,
Иногда это записывают в форме, как для упругого случая
Конкретные расчеты существенно усложняются, поэтому наряду с аналитическими методами широко пользуются графическими, графоаналитическими и численными методами решения. 2.16.2. Расчет по предельным нагрузкам. В качестве примера рассмотрим элементы расчета статически неопределимых систем, элементы которых работают на растяжение (сжатие). Расчеты на прочность, рассмотренные выше, выполнялись по допустимым напряжениям (по опасной точке). При таком подходе к расчету прочность конструкции считается нарушенной, если хотя бы в одной ее точке (опасной) расчетное напряжение окажется равным предельному напряжению sпп или sт, или sв. Соответственно в качестве допустимой нагрузки конструкции принимается такая, при которой расчетное напряжение в опасной точке конструкции равно допускаемому напряжению Таким образом, в пределах упругих деформаций допускаемая нагрузка в k раз меньше той, при которой в опасной точке расчетное напряжение становится равным предельному напряжению для данного материала. Рассмотрим принципиально иной подход к расчету на прочность применительно к конструкциям из пластичных материалов при действии статических нагрузок. При этом подходе предельной нагрузкой F пред конструкции считается такая, при которой система перестает быть геометрически неизменяемой и теряет способность сопротивляться возрастанию нагрузки. Допускаемая нагрузка [ F ] назначается как некоторая часть от предельной
При расчете будем исходить из схематизированной диаграммы (рис. 47)
Рис. 47
Расчеты по [s] и по F пред приводят к различным результатам в случаях, когда напряжения в поперечных сечениях элементов конструкции распределены неравномерно (например, при изгибе или кручении) и в тех случаях, когда система статически неопределима (даже при равномерном распределении напряжения). Для статически определимых систем (рис. 48), элементы которых работают на растяжение (сжатие), результаты расчета по обоим методам совпадают. Например, для сиcтемы, показанной на рис. 34, при расчете по допускаемым напряжениям нагрузка должна быть в n раз меньше той, при которой в наиболее нагруженном стержне (при b<a в стержне ВС) возникает текучесть. Очевидно, что при возникновении текучести в одном стержне система становится геометрически изменяемой, т. е. нагрузка, вызывающая текучесть в наиболее нагруженном стержне является предельной для нагрузки в целом, и, следовательно, допускаемая нагрузка [ F ], определенная из расчета по предельной нагрузке, будет такой же, как и в первом случае.
Рис. 48
В статически неопределимой системе (рис. 49) текучесть в первую очередь возникает в наиболее нагруженном стержне. Раскроем статическую неопределимость, для чего запишем условия совместности удлинений стержней
Рис. 49
По закону Гука Условие равновесия Откуда Таким образом Найдем силу F Т, при которой в среднем стержне возникает текучесть
и
При расчете по допускаемым напряжениям эта сила рассматривается как опасная (условно предельная) и допускаемая нагрузка системы определится из условия
При силе, равной F т, несущая способность конструкции не исчерпана, так как стержни 1 и 3 находятся в упругом состоянии и оказывают сопротивление возрастающей нагрузке. При силе, большей F т, усилия N 1 и N 2 могут быть найдены из уравнений равновесия, так как усилие N 2 сохраняет постоянное значение, равное Предельная нагрузка может быть найдена и без раскрытия статической неопределимости системы и анализа упругой стадии ее работы. Для определения F пред в рассмотренном случае достаточно принять, что усилие в каждом из стержней равно
2.16.3. Элементы теории ползучести. Форсирование режимов работы промышленных аппаратов и устройств, повышение рабочих параметров энергетических установок нуждается в решении ряда задач, связанных с жаропрочностью. Одной из таких задач является построение методов расчета напряжений и деформаций материалов и элементов конструкций, работающих при высоких (повышенных) температурах в разных условиях нагружения. Применение легких сплавов делает эту проблему еще более актуальной, так как здесь ползучесть заметно проявляется при довольно низких температурах. Быстрое развитие химии полимеров, характер деформирования которых при обычной температуре совпадает с характером высокотемпературного деформирования металлических материалов, также требует развития методов расчета на прочность и деформируемость. Феноменологически явление ползучести состоит в самопроизвольном развитии деформации во времени при постоянном значении напряжения. Оно проявляется для обычных машиностроительных сталей при температурах порядка 400–500°С, для специальных жаропрочных материалов при температурах 500°С и выше, для легких сплавов и цветных металлов при 50–150°С. Полимеры проявляют реономные свойства уже при комнатной температуре. Общий характер деформирования при ползучести ясен из рис. 50. Если в упругом случае при нагружении тела в нем появляются только упругие деформации, при работе конструкции в области пластичности развиваются уже две составляющие общей деформации – упругая и пластическая, то при работе в условиях ползучести полная деформация складывается из трех компонент упругой
Рис. 50
Итак, если призматическое тело нагружено продольным напряжением, то на выходе такой системы можно различить три элемента В момент времени t= 0 вся деформация является упругой. С течением времени полная деформация растет и превосходит упругую деформацию, остающуюся неизменной во времени. Если в какой-то момент времени t=t 0 нагрузка была снята, то происходит так называемый возврат деформации. При этом упругая часть
Рис. 51
Желая оставаться на феноменологическом уровне, придется определять вид правых частей этих уравнений экспериментальным путем, т. е. строить на основе опытов две функции трех переменных. Большое число устройств, работающих в условиях ползучести, находится под нагрузкой длительное время (сотни и тысячи часов). В этих условиях основной вклад в деформацию ползучести дает остаточная компонента деформации
где А – некоторый оператор. При относительно высоких напряжениях деформация на II (наиболее длительном) участке ползучести (так называемом участке установившейся ползучести) растет с почти постоянной скоростью
где Обратим внимание еще на одно обстоятельство, полезное для размышлений. Нелинейная зависимость σ от ε (как в случаях пластического деформирования, ползучести) может быть обусловлена не переменными реологическими коэффициентами (например, модулем упругости, физическая нелинейность), но различными способами определения деформаций, геометрическая нелинейность. Не существует единой меры деформации. Пусть растягиваемый призматический элемент длиной
Если деформация бесконечно мала, то в соответствии с мерой деформации Коши имеем
где λ – степень растяжения. Можно это выражение обобщить и н конечные деформации
Но в качестве меры деформации можно использовать любую функцию от λ при условии, что она: 1. обращается в нуль при λ=1 и 2. сводиться к деформации (*), когда λ – 1 бесконечно мала; 3. является безразмерной величиной (это нужно, чтобы деформация не зависела от размеров тела). Все эти условия выполнены для определения деформации, предложенной Свейнгером, Грином, Алманси и Хенки. Они выглядят так
Чтобы оценить разницу между этими определениями допустим, что длина стержня увеличилась в два раза. Тогда:
Для всех этих определений могут быть составлены тензорные уравнения. Итак, основным следствием ползучести является изменение формы элементов конструкции. Если напряжение и температура распределены неравномерно, то деформации ползучести различны по отдельным элементам конструкции, и в результате форма их искажается. Другим следствием ползучести является изменение начального распределения напряжений в конструкции, поскольку деформации ползучести изменяются во времени и, следовательно, зависят не только от напряжения. Среди материалов, используемых в технике, особенно заметно ползут дерево, бетон, мягкие стали. Ползучесть тканей – одна из причин, по которым одежда теряет свою форму. Перекосы, вызванные ползучестью в старых деревянных конструкциях, особенно бросаются в глаза. В зданиях зачастую живописно оседают крыши. Грунты и горные породы, подобно другим материалам, также подвержены ползучести. Поэтому требуется следить за оседанием фундаментов зданий. Вследствие ползучести напряжения в материале некоторым образом перераспределяются, и это может играть и положительную роль. Еще одним следствием ползучести является релаксация (уменьшение) напряжений. Релаксацией напряжений называется самопроизвольное уменьшение напряжений при неизменной во времени общей деформации. Например, ослабление затяжки болтового соединения (рис. 52), s0 – начальное напряжение затяжки.
Рис. 52
Релаксация является частным случаем ползучести и описывается теми же уравнениями. Ползучесть как случайный процесс. Как известно, многие явления в жизни и технике носят "случайный" (стохастический) характер. Однако во многих прочностных задачах разброс механических характеристик относительно не велик и им часто пренебрегают. В условиях ползучести материалов с ним надо считаться. Значительный разброс экспериментальных данных при испытаниях материалов на ползучесть отмечается многими авторами. Это говорит о том, что наличие разброса в условиях ползучести является, по-видимому, общей закономерностью, которую нельзя игнорировать.
Это обстоятельство существенно отличает ползучесть от теории упругости и пластичности, где разброс обычно не велик и часто может вообще не рассматриваться. Типичный разброс кривых ползучести (10 повторных испытаний) показан на рис. 53.
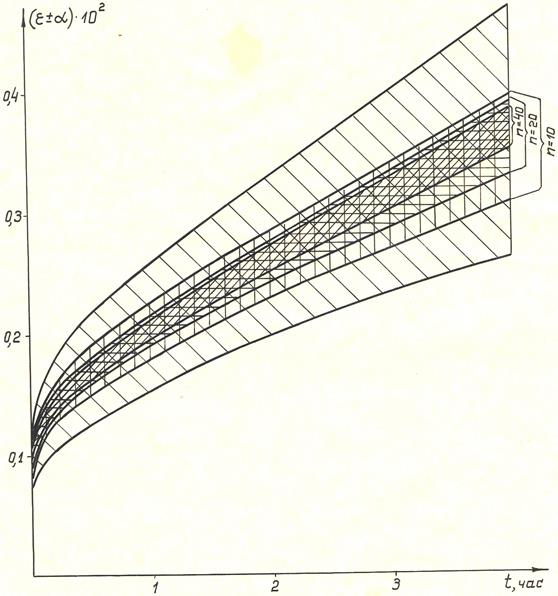
Рис. 53 Чувствуя недостаточную надежность опытных данных, авторы иногда указывают число повторов рассматриваемого опыта и приводят осредненные результаты. Однако простым осреднением такие вопросы разрешить, конечно, нельзя. Из сказанного следует, что все экспериментальные данные должны содержать не только осредненные кривые, но и соответствующие доверительные полосы (полосы разброса). На рис.54 показана типичная зависимость ширины доверительной полосы от числа экспериментальных поворотов (расчет сделан для доверительной вероятности 0,95).
Рис. 54 И, наконец, несколько замечаний о формировании уравнений, описывающих ползучесть. Для формулирования тех или иных уравнений ползучести на феноменологическом уровне всегда приходится некоторые константы или функции определять по экспериментальным данным. При этом принято, как уже отмечалось, использовать осредненные кривые ползучести, полученные на основе нескольких реализаций. Точность, с которой найдены таким способом параметры или функции, не оценивается. Из рисунка видно, что доверительная полоса при небольшом числе реализаций довольно широка, и необходимые величины нельзя надежно вычислить по осредненной кривой. Это обстоятельство необходимо учитывать при сравнении феноменологических уравнений ползучести с другими экспериментальными данными, так как в противном случае можно необоснованно забраковать вполне «хорошие» уравнения. Именно доверительные полосы содержат те необходимые данные, без которых невозможно правильно оценить правдоподобие тех или иных уравнений ползучести. В работах по ползучести этого делать не принято, и поэтому до сих пор отсутствуют какие либо критерии для оценки правильности тех или иных гипотез. Наблюдаемые расхождения теории и эксперимента авторы, как правило, относят за счет разброса экспериментальных данных, хотя совершенно очевидно, что такие ссылки почти ни о чем не говорят. Далее, в литературе по ползучести встречаются случаи, когда теория и эксперимент согласуются очень хорошо, хотя неизвестные параметры найдены всего по трем-пяти реализациям. Такие совпадения при наличии заметного разброса являются весьма маловероятными, и их появление может вызвать только недоверие к использованной методике. Вопрос о необходимом числе исходных реализаций решается требуемой точностью. Например, для грубых расчетов можно ограничиться десятью реализациями, а сорок реализаций, видимо, позволят давать довольно точные прогнозы о деформациях. Если взять число реализации меньше десяти, то точность определяемых параметров может оказаться недопустимо низкой, и почти любые управления ползучести будут выглядеть как вполне правдоподобные. Изложенные соображения относятся к детерминистским уравнениям ползучести, в которые входят только математические ожидания различных случайных величин или случайных функций. Не отрицая важности такого подхода, все же нетрудно видеть, что с его помощью решить вопрос о закономерностях в разбросе кривых ползучести нельзя. Действительно, введение средник величин, по своему существу, направленно на то, чтобы отвлечься от разброса и установить некоторые объективные закономерности, справедливые для достаточно больших коллективов экспериментальных данных. Очевидно, что решение такой задачи невозможно в рамках обычных детерминистских уравнений, в которые не закладывается никакой информации о величине рассеивания опытных данных. Поэтому следует перейти к рассмотрению более общих, стохастических уравнений, в которые входили бы случайные величины или случайные функции, способные описать разброс кривых ползучести. И еще: 1. Разброс экспериментальных данных о ползучести зависит также от длины той базы, на которой измеряется деформация (сказывается локальность развития деформации ползучести). 2. Для деталей малой протяженности разброс кривых ползучести может быть очень большим, и такие детали могут обнаружить "непредусмотренное" разнообразие при испытаниях на ползучесть. 3. При сложном напряженном состоянии влияние локальности деформаций может оказаться особенно большим; например, если в задаче о концентрации напряжений вблизи вершины выточки (впадины) окажется "склонный" к ползучести элемент, то напряжение в этом месте быстро упадет, если же этот элемент такой "склонности" иметь не будет, то указанное напряжение окажется слабо убывающим или даже возрастающим. Таким образом, два однотипных элемента конструкции за счет разброса могут получить различные деформации со значительным отклонением в плюс и минус от предсказанного математического ожидания. Такие отклонения способны пагубно влиять на работу всей конструкции, хотя быть может средние значения накопленных деформаций по большому коллективу рассматриваемых элементов лежат все время в допустимых пределах. Отсюда ясно, какое большое значение играет разброс опытных данных для оценки работоспособности различных конструкций. В связи с этим должна рассматриваться задача о предсказании не только средних значений накопленных деформаций, но и их возможной полосы разброса. 2.16.4. Длительная прочность. Длительной прочностью называется явление разрушения материала (элемента конструкции) во времени при неизменном напряжении (нагрузке), рис. 55. Это явление, так же, как и ползучесть, заметно проявляется при повышенных температурах.
Рис. 55
Аналитических зависимостей для описания длительной прочности (зависимости времени до разрушения от напряжения t=f(s)) предложено достаточно много, но процесс формирования методов расчета еще далеко не закончен. 2.16.5. Приспособляемость. Пусть тело нагружено некоторой системой переменных внешних усилий Если можно найти такое распределение самоуравновешенных внутренних напряжений Пример. Сплошная балка постоянного сечения нагружена как показано на рис. 56. Обозначим через На центральной опоре
в точке А
Рис. 56
Если не учитывать приспособляемости, максимальное значение F, соответствующее
Обозначим через MC момент приспособляемости на опорах; должно выполняться условие
Откуда
и
Тогда
После приспособления максимальное значение F оказывается равным
Отношение В общем случае поведение такой балки, нагруженной системой неизменных нагрузок и некоторыми переменными догрузками, будет чисто упругим, если в любом сечении выполнены условия
где Если эти неравенства не удовлетворяются, балка, тем не менее, будет сохранять работоспособность, если только можно найти такой момент
Момент приспособляемости полностью определяется своими значениями на опорах. Поскольку график данного момента является разрывным, в опорных сечениях можно увидеть, удастся ли провести новую новую кривую-диаграмму моментов, значения которых всюду превосходят предельные значения моментов. Если это так, балка может приспособляться. 2.16.6. О надежности и долговечности машин. С вопросами длительной прочности смыкаются задачи теории надежности и долговечности машин и вообще инженерных устройств, получившей в последние годы значительное развитие. Это большая и, в значительной мере, самостоятельная область инженерной деятельности. В силу понятных причин мы не будем ее специально рассматривать, ограничившись несколькими базовыми замечаниями. Утрата машинами (любыми инженерными сооружениями) своих эксплуатационных свойств с течением времени носит на первый взгляд случайный характер, поэтому для анализа надежности и долговечности машин и механизмов применяются также методы теории вероятностей и математической статистики. В теории надежности и долговечности машин и сооружений под событием, составляющим изучаемое явление, подразумеваются различные виды утрат деталями машин работоспособности, приводящие к выходу их из строя или, как говорят, к отказу. Под частостью появления отказов подразумевается отношение числа m вышедших из строя деталей к общему числу деталей n, составляющих исследуемую партию. На основе статистической обработки действительных сроков службы партии машин или их деталей, т.е. на основе частостей отказов, устанавливаются теоретические вероятности, служащие для прогнозов на будущее. При практических расчетах частость
находится вероятность невыхода P(t) из строя деталей или, как говорят, их надежность. При расчете на надежность и долговечность всякая машина считается состоящей из ряда функциональных цепей. Каждая из них предназначается для выполнения определенных функций, которые в совокупности обеспечивают работоспособность машины в целом. Если детали функциональной цепи соединены таким образом, что выход из строя только одного звена (детали) препятствует дальнейшему функционированию всей цепи, то такое соединение называется последовательным. Очевидно, что при таком соединении, состоящим из n звеньев, надежность состоит из невыхода из строя всех деталей
где p – вероятность выхода из строя любого одного звена. При параллельном соединении цепь будет работать и при выходе из строя одной детали и, следовательно, надежность определится как
т. е. при увеличении числа деталей, соединенных последовательно, надежность понижается, а при параллельном – повышается. Однако в подавляющем большинстве случаев детали в функциональных цепях, как и сами цепи, соединены последовательно. Основные положения теории надежности следующие: 1. Bce детали машин со временем и по мере использования машин, в которых они установлены, теряют свои первоначальные физические свойства. Долговечность машин зависит от долговечности наиболее быстроизнашивающихся деталей, которая неизбежно зависит от воспринимаемых ими нагрузок и других эксплуатационных воздействий. 2. Надежность, т.е. вероятность безотказной работы деталей машин тем выше, чем меньше расчетный (проектный) срок службы по сравнению с медианным, т.е. сроком, который при заданных условиях использования выдержало бы не менее 50% деталей. Таким образом, параметрами надежности и долговечности деталей машин могут явиться нормативные значения медианных сроков службы при соответствующих нормативных значениях нагрузочных воздействий, под которыми подразумеваются силы, напряжения, удельные давления, моменты и другие воздействия, приводящие к утрате деталями машин своих первоначальных физических свойств работоспособности. Как уже отмечено, к важнейшим понятиям надежности относится долговечность, показателем которой является срок службы, ресурс. Сейчас начинает доминировать точка зрения, согласно которой временные показатели надежности более содержательны, чем традиционные показатели безотказности (вероятность безотказной работы, интенсивность отказов). Предпочтительность долговечности, как характеристики надежности, особенно ощущается в тех случаях, когда отказы связаны с совершающимися во времени процессами накопления повреждений, пластических деформаций, износа, деградации свойств материалов, обусловленной диффузией, сорбционными явлениями, рекристаллизацией, электромиграцией, старением (например, металлов, полупроводников, полимеров) и т. д. Известно, что подобные явления (накопление повреждений в широком смысле) вызывают приблизительно 80% всех отказов. Поэтому определение долговечности можно считать одной из основных практических задач теории надежности в настоящее время. Как известно, проблема надежности относится к числу так называемых «вечных» проблем, которые на каждом новом этапе развития техники возникают в новой постановке. Поскольку экспериментальное определение надежности деталей машин основано на статистической обработке результатов массовых испытаний деталей машин на долговечность, то очевидно, что режимы этих испытаний должны быть значительно форсированы, т. е. укорочены по сравнению с эксплуатационными по основному нагрузочному воздействию, так как испытания на эксплуатационных режимах могут безнадежно затянуться, они дороги, технически трудно осуществимы и нередко лишены практического смысла из-за быстрой смены поколений изделий техники. Поэтому можно полагать, что прогнозирование долговечности с помощью расчетных методов (например, на основе анализа данных форсированных испытаний, использования какой-либо априорной информации вероятностного или физического характера и т. п.) является предпочти тельным подходом - особенно на стадии разработки и внедрения изделия или материала. Говоря о тенденции развития современной теории надежности можно назвать два методологически разных направления: вероятностностатистическое (<<математическое») и причинно-следственное (<<физическое»). Эффективность рекомендаций по надежности на этапах разработки и производства при применении методологии причинно-следственного подхода существенно выше, поскольку в этом случае используется исходная информация более высокого иерархического уровня, чем апостериорная информация о числе отказов. Однако методология вероятностностатистического исхода обладает большей эффективностью в тех случаях, когда исследуются изделия, имеющие сравнительно невысокий уровень надежности и нет необходимости детально изучать конкретные причины и механизмы отказов Еще раз обратим внимание на то обстоятельство, что для многих устройств следует считать отказами не только полную потерю работоспособности, т. е. катастрофические отказы, но и уход технологических параметров элементов за допустимые пределы (снижение «качества»), т. е. nараметрuческuе отказы. Наконец, нужно иметь в виду, что чем выше потенциальная надежность изделия, тем сложнее задача определения его долговечности. Для решения этих задач, как отмечалось, предложены разные подходы, рассматривать которые мы не имеем возможности, и ограничимся несколькими замечаниями. В терминах принятого нами общего феноменологического подхода (использующего теорию управления сложной системой) кинетика деградационной повреждаемости материала или элемента конструкции может быть описана интегральным уравнением Вольтерры I рода относительно скорости процесса. Последние исследования показали, что для получения информации о функции повреждаемости («входные» данные для указанного уравнения) нужно проводить испытания образцов в двух режимах ступенчатого повышения нагрузки. В этом случае образцы, проэкспонированные в течение некоторых (небольших) отрезков времени в рабочем режиме, доводят до отказа при форсированной нагрузке, регистрируя время действия последней; два режима испытаний отличаются друг от друга уровнем форсированной нагрузки при постоянстве рабочей нагрузки. Следовательно, необходимо решить следующие две задачи: 1. Определить наивысший предельный уровень форсирования нагрузочного воздействия, при котором физические явления утраты работоспособности еще не выходят за пределы явлений, характерных для работы в условиях нормальной эксплуатации. 2. Произвести пересчет параметров надежности, полученных на основе обработки результатов при форсированном режиме, на параметры, соответствующие режимам нормальной эксплуатации.
МЕТАЛЛОКОНСТРУКЦИИ
Металлоконструкции широко применяются при строительстве: несущие конструкции зданий, мосты, подъемные краны и др. При расчете металлоконструкций по возможности учитывают все действующие на них нагрузки: постоянные и подвижные, ветровые, от собственного веса. Расчет ведется на наиболее неблагоприятное сочетание нагрузок. Материалы металлоконструкций. Meталлоконструкции изготавливаются в основном, из стальных листов и стального фасонного проката. Он остирован. С целью снижения веса тяжелых конструкций можно использовать низколегированные стали. Для получения более легких конструкций находят применение и легкие сплавы (алюминиевые и магниевые). Их основные достоинства: малый удельный вес (в 2 - 3 раза меньше стали), высокая коррозионная стойкость. Однако вследствие меньшего модуля упругости алюминиевых сплавов критическая сила для сжатых алюминиевых стержней ниже, чем для стальных. Поэтому сжатые алюминиевые стержни следует конструировать более жесткими (коробчатого или трубчатого сечения). Необходимость применения тех или иных материалов в каждом отдельном случае должна быть обоснована, техническими или экономическими соображениями. Типы металлоконструкций показаны, например, на рис. 57. Методы расчета. Статический расчет металлоконструкций производят методами строительной механики. При расчете используется принцип независимости действия сил. При точных расчетах ферменных конструкций, возникающие в элементах конструкции усилия определяются как для пространственной системы. Однако возможно упрощение метода, основанное на расчленении пространственной металлоконструкции на отдельные плоские системы (главная ферма, вспомогательные фермы, концевые балки и т.д.), каждая из которых рассматривается под действием сил в соответствующих плоскостях.
|
|||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 572; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.21.5 (0.097 с.) |
 .
. , где
, где  .
. .
. .
.


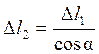 ,
,  .
. .
. .
. ;
;  .
. .
.
 .
.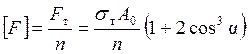 .
.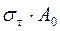 .
. .
. , остаточной
, остаточной  и деформации упругого последействия
и деформации упругого последействия  , медленно исчезающей после снятия нагрузки,
, медленно исчезающей после снятия нагрузки,

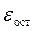 и
и  .
.

 ,
, =const и появляется возможность еще более упростить ситуацию и описать рост деформации относительно простым выражением
=const и появляется возможность еще более упростить ситуацию и описать рост деформации относительно простым выражением ,
, – скорость деформации, В и n – экспериментальные постоянные.
– скорость деформации, В и n – экспериментальные постоянные. поле деформации имеет длину
поле деформации имеет длину
 (*)
(*)
 и нет изменения длины;
и нет изменения длины;




 . Если бы поведение тела было при любых значениях нагрузок упругим, произвольному состоянию системы
. Если бы поведение тела было при любых значениях нагрузок упругим, произвольному состоянию системы  соответствовало напряженное состояние
соответствовало напряженное состояние  .
. (напряжений приспособляемости), для которых суперпозиция
(напряжений приспособляемости), для которых суперпозиция  и
и  в любой точке тела приводит к некоторому упругому состоянию, устойчивость тела будет обеспечена; при этом значения остаточных напряжений стремятся к значениям напряжений приспособляемости (остаточные напряжения – остающиеся в теле после разгрузки).
в любой точке тела приводит к некоторому упругому состоянию, устойчивость тела будет обеспечена; при этом значения остаточных напряжений стремятся к значениям напряжений приспособляемости (остаточные напряжения – остающиеся в теле после разгрузки). предельное значение момента. Требуется чтобы выполнялось условие
предельное значение момента. Требуется чтобы выполнялось условие  Приложенные силы могут меняться от 0 до некоторого предельного значения Fn. Упругий расчет дает:
Приложенные силы могут меняться от 0 до некоторого предельного значения Fn. Упругий расчет дает:





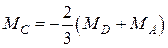 ,
, .
. ,
,  .
. .
. к F` дает 1,125
к F` дает 1,125
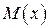 и
и  – огибающая диаграмма изгибающих моментов;
– огибающая диаграмма изгибающих моментов;  и
и  – предельные значения моментов.
– предельные значения моментов. , для которого
, для которого
 обычно отождествляется с вероятностью p(t), где t – время, в течение которого вышли из строя m деталей. Из соотношения
обычно отождествляется с вероятностью p(t), где t – время, в течение которого вышли из строя m деталей. Из соотношения
 ,
,



