
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Более общие методы решения прочностных задач. Численные методы
Как мы уже знаем, задачи определения напряжений вы нагруженных элементах конструкций являются внутренне статически неопределимыми, т.е. уравнения статики не позволяют найти характер распределения напряжений в опасных сечениях, что необходимо для решения вопроса о прочности. А задаться особенностями такого распределения, как это делалось в задачах упругого кручения и изгиба стержней, в большинстве практических случаев не представляется возможным. Это было видно, например, в задаче о концентрации напряжений при наличии всевозможных выточек, резком переходе сечений и пр. Обойти это затруднение позволяет общая теория напряженно-деформированного состояния. Чем более общий характер носит метод, разработанный для решения прочностных задач (в принципе это справедливо в любой области. Еще древние говорили, что надежность истины пропорциональна ее общности), тем он более надежен. Тем менее приходится вводить в решение частные предпосылки суживающие область применения решения. Частные методы приходится применять тогда, когда не удается сформулировать более общий подход, обеспечивающий большую глубину постановки задач. В ряде случаев получение точного решения прочностных задач наталкивается на большие математические трудности. Поэтому приходится прибегать к численным методам. Численное решение принципиальных трудностей не представляет, поскольку для этого существуют стандартные программы. И, следовательно, основной задачей в этом случае является формирование аппроксимирующей системы линейных уравнений. С математической точки зрения это означает переход к модельной линейной системе с разрывными кусочно-постоянными коэффициентами. В общем случае напряженного состояния используются тензорные величины, обозначаемые как и их скалярные аналоги. Тензором второго ранга принято называть объект, который в трехмерном декартовом пространстве определяется таблицей из девяти величин aij, где i, j =1,2,3, если при преобразовании одной декартовой системы координат в другую эти величины изменяются по закону
Здесь λij – направляющие косинусы осей второй системы по отношению к первой. По определению скаляр – это тензор нулевого ранга, вектор-тензор первого ранга. Тензор второго ранга в фиксированной системе координат имеет 9 компонентов, которые могут быть записаны в виде матрицы. Вообще говоря,
Компоненты напряжений Выделим из деформированного тела малый кубический элемент с гранями, параллельными координатным осям (рис. 113).
Рис. 113 Обозначения для компонент напряжений, действующих на гранях этого элемента, а также направления, которые считаются положительными, показаны также на рис. 113. Касательные напряжения разлагаются на две компоненты, параллельные координатным осям. Тогда, чтобы обозначить напряжения, действующие на шести гранях элемента, потребуются три символа sx, sy и sz для нормальных напряжений и шесть txy, tyx, txz, tzx, tyz, tzy – для касательных. С помощью простой процедуры исследования равновесия элемента число символов для касательных напряжений можно сократить до трех. Из условия
Элементы тензора (s) связаны уравнениями равновесия
Три уравнения содержат шесть неизвестных sx, sy и sz, txy=tyx, txz=tzх, tzу=tyz. Следовательно, задача об определении напряжений как функций координат деформируемого тела является статически неопределимой. Эта неопределенность раскрывается путем учета физических свойств деформируемого тела. Компоненты деформаций Разложим перемещения частиц деформированного тела на компоненты U, V и W, параллельные соответственно координатным осям x, y и z. Эти компоненты малы и меняются непрерывно по объему тела. В данном случае нас не интересует анатомическая структура деформируемого тела и будем считать, что вещество заполняет его непрерывно (как говорят, тело обладает сплошностью). Цель этого допущения состоит в использовании вычислительных упрощений, которые дает анализ бесконечно малых при изучении непрерывных функций. Рассмотрим малый элемент упругого тела (рис. 114).
Рис. 114
Если тело деформируется и U, V и W – компоненты перемещения в точке Р, то перемещения в направлении х в точке А, расположенной на оси х, с точностью до величины первого порядка по dх будут
ввиду возрастания функции U на величину
Таким образом, относительное удлинение в точке Р в направлении х составит
Аналогичные рассуждения дадут также выражения деформаций сдвига
Итак
Шесть величин ex, ey, ez, gxy, gyz, gzx называются компонентами деформации. Совокупность этих компонент образует тензор деформации
Элементы тензора (e) должны подчиняться уравнениям совместности (неразрывности, условию сплошности тела). Дифференцируя попарно компоненты в (7.3) и исключая члены, содержащие производные от U, V и W, получим эти уравнения
Уравнения совместности носят общий характер в том смысле, что они позволяют для раскрытия статической неопределенности уйти от предварительных предположений о характере распределения напряжений в опасных сечениях, как это делалось, например, при расчетах на кручение и изгиб.
|
||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 151; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.136.235 (0.006 с.) |
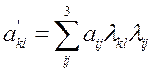
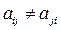 . В частном случае, когда
. В частном случае, когда 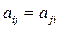 , тензор называют симметричным. Тензор напряжений и представляет собой ортогональный симметричный тензор второго ранга.
, тензор называют симметричным. Тензор напряжений и представляет собой ортогональный симметричный тензор второго ранга.
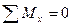 следует
следует 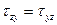 . Аналогично получим
. Аналогично получим 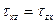 и
и 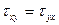 . Полученный результат выражает закон сопряженности или взаимности касательных напряжений. Таким образом, тензор напряжений изображается так
. Полученный результат выражает закон сопряженности или взаимности касательных напряжений. Таким образом, тензор напряжений изображается так . (7.1)
. (7.1)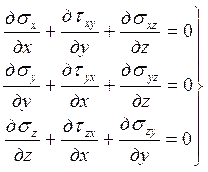 . (7.2)
. (7.2)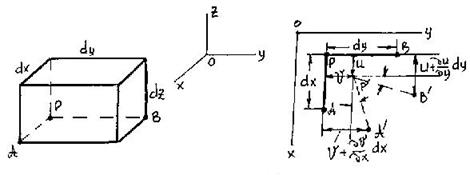
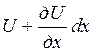 ,
,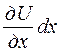 с увеличением координаты х. Увеличение длины РА, вызванное деформацией, равно
с увеличением координаты х. Увеличение длины РА, вызванное деформацией, равно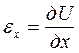 . Подобным образом относительные удлинения в направлениях у и z соответственно будут
. Подобным образом относительные удлинения в направлениях у и z соответственно будут и
и  .
. ,
,  ,
, 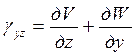 .
.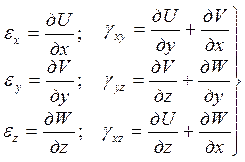 . (7.3)
. (7.3)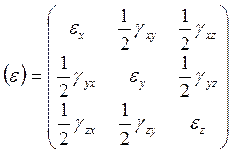 . (7.4)
. (7.4)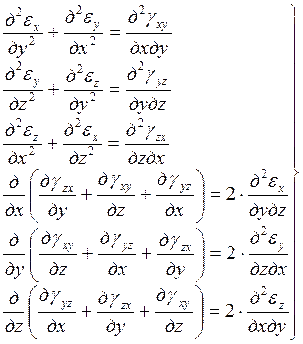 . (7.5)
. (7.5)


