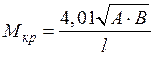Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Устойчивость равновесия упругодеформированных систем
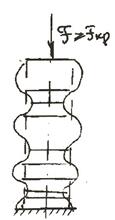
Как уже отмечалось, при расчетах на прочность нормируются величины напряжений, возникающих в элементах конструкции при работе. Если нормируются перемещения, то выполняются расчеты на жесткость. Но иногда оказывается, что помимо указанных расчетов есть необходимость в рассмотрении вопросов устойчивости равновесия принятой формы проектируемых элементов конструкций. Пусть некоторая механическая система находится в равновесии. Мысленно сообщим точкам этой системы бесконечно малые скорости и рассмотрим ее движение под действием приложенных сил (возмущенное движение). Если с неограниченным возрастанием времени отклонения системы от равновесного положения остаются бесконечно малыми, то рассматриваемое равновесие называется устойчивым. В противном случае неустойчивым. Устойчивость сжатого стержня. Наиболее простой и часто встречающейся инженерной задачей устойчивости упруго деформированной системы является устойчивость сжатого стержня. В таких условиях работают всевозможные колонны, опоры, стержни ферм мостов, подъемных кранов, перекрытий строительных конструкций и т. п. При действии осевой сжимающей силы на длинный и достаточно тонкий стержень может произойти его искривление, т. е. продольный изгиб (рис.42).
Рис. 42
То наибольшее значение сжимающей силы, при котором стержень еще остается прямым, или то наименьшее значение сжимающей силы, при котором стержень может начать искривляться, называется критической силой F кр. Значение F кр в соответствии с решением, данным Л. Эйлером, равно
Нужно иметь в виду, что величина критической силы зависит от способа закрепления стержней, который можно учесть некоторым «коэффициентом закрепления» m. Тогда
Формулой Эйлера можно пользоваться при условии, что напряжения, возникающие при действии F кр, меньше предела пропорциональности материала стержня. Еще одним примером потери устойчивости может служить явление бокового опрокидывания балки, сопровождающееся ее закручиванием: оно может иметь место для узких балок без бокового опирания при некотором критическом значении внешней нагрузки, значительно меньшим тех значений, при которых исчерпывается работоспособность на изгиб балки с боковыми опорами. Например, консоль с силой на конце (рис.43). Критическая нагрузка
Рис. 43
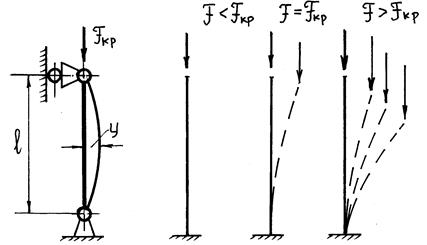
где А и В – жесткости на боковой изгиб и кручение, соответственно. Этой нагрузке соответствует критический момент
При равномерно распределенной нагрузке
Еще пример (рис. 44). Свободно опертая балка постоянного сечения в форме прямоугольника (предполагается, что крайние сечения балки не могут поворачиваться относительно продольной оси).
Рис. 44 Вообще говоря, многие крупногабаритные технические конструкции могут быть описаны с помощью потенциальной функции, минимальное значение которой определяет локально устойчивое состояние конструкции. Само состояние описывается положением точки в некотором пространстве состояний конструкции. С увеличением нагрузки на конструкцию (мост, здание и т.д.) потенциальная функция изменяется. Значит, нагрузка может привести к потере устойчивости (т.е. к ее разрушению) вследствие нарушения локально-устойчивого состояния, которое является для данной системы расчетным. В широкой постановке равновесие, устойчивость и потеря устойчивости рассматриваются математической теорией катастроф. Ее методы позволяют определить чувствительность критической или разрушающей нагрузки, как несовершенству конструкции, так и к динамическому воздействию. Они оказываются эффективными при изучении составных систем, для которых возможны различные виды разрушения. Последнее обстоятельство имеет важное практическое значение, т.к. свидетельствует о том, что в «оптимизационных» системах, составленных из нескольких конструкционных элементов, могут появиться неожиданные формы разрушения с жесткой чувствительностью к несовершенству, если между элементами существует сильная связь (например, разрушения опорных кронштейнов и пр.). Изменения в очень многих случаях совершаются скачком (рис.45). Эти внезапные изменения вызываются обычно гладкими изменениями ситуации. Такие внезапные изменения и были названы «катастрофами» для того, чтобы отразить ощущение резкой и драматической перемены. Теряют устойчивость арки, пластины, оболочки (гофрируются).
Как оказалось, даже простые задачи классической статики таят в себе много тонкостей. Анализ обнаруживает некоторые, лежащие в основе этих явлений, математические закономерности, позволяющие стандартным образом рассчитывать поведение таких систем.
Замечание о прочности материалов при быстро меняющихся нагрузках. Опыт показывает, что сопротивление материалов быстро меняющимся нагрузкам (деформациям) несколько отличается от сопротивления деформациям, протекающим очень медленно, «статически». Обнаружено следующее: 1) с повышением скорости деформирования предел упругости (текучести) возрастает; 2) динамические модули упругости мало отличаются от статических значений для тел с кристаллической структурой. В телах органических с высокомолекулярной структурой (резина, пластики, высокие полимеры) влияние скорости деформирования заметно в пределах упругости; 3) предел прочности растет с увеличением скорости деформации и разрушение происходит более хрупко. Диаграмма растяжения показана на рис. 46
Рис. 46
|
||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 223; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.88.130 (0.009 с.) |
 .
. .
.