
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
В.6. Свойства пространства и времени в классической механике
Пространство характеризуется своими топологическими и метрическими свойствами. Пространство в классической механике бесконечно делимо: допускается существование сколь угодно малых пространственных промежутков (в квантовой механике устанавливается предел дробления: минимальная «планковская» длина имеет порядок Пространство в классической механике является евклидовым. Квадрат длины бесконечно малого пространственного промежутка равен
Пространство однородно (отсутствуют «избранные» места) и изотропно (отсутствуют «избранные» направления). Метрические свойства фигур - расстояния между их точками и углы - не меняются при параллельном переносе фигур в пространстве, при повороте и зеркальном отражении от плоскости. Время бесконечно делимо, однородноиоднонаправлено. В каждой новой задаче механики отсчет времени чаще всего начинается с нуля: Свойства пространства и времени («пространства-времени») и физические законы взаимно соответствуют друг другу. Пространство специальной теории относительности – псевдоевклидово пространство Минковского. Пространство общей теории относительности – риманово пространство. Эйнштейн в своих популярных лекциях предлагал представить себе наше пространство как трехмерный аналог расширяющейся сферы, конечной, но безграничной. Существуют различные модели эволюции вселенной. Эруптивные модели представляют развитие Вселенной результатом распада (эрупции) некоторого протовещества. Согласно дисперсным моделям эта эволюция есть следствие «рассыпания» сингулярной точки на множество первичных элементов вещества. Например, IλCDM (Inflationary Lambda Cold Dark Matter model) – инфляционная модель (дисперсионная, предполагающая быстрое раздутие – инфляцию – Вселенной сразу после Большого Взрыва) с λ – членом и холодным тёмным веществом. Космологическая постоянная λ характеризует современное ускорение расширения Вселенной. Тёмное (не наблюдаемое в опытах) вещество вместе с «тёмной энергией» антигравитации составляют, как считают физики, 95% Вселенной.
В.7.Система отсчета - физическое тело (чаще всего твердое тело), относительно которого рассматривается движение изучаемых объектов. Предполагается, что система отсчета всюду оборудована часами. В.8.Обобщенные координаты механической системы – это взаимно независимые скалярные величины, однозначно определяющие положение системы в пространстве относительно заданной системы отсчета. Назначить обобщенную координату означает задать: а) начало её отсчета, б) направление отсчета, в) способ отсчета. Обобщенные координаты часто имеют смысл неких расстояний или углов. В.9. Числом степеней свободы (подвижности) механической системы условимся называть количество её обобщенных координат. В.10. Связи – ограничения (условия), накладываемые на движение механической системы. Эти ограничения могут быть заданы, например, графически в виде схематических рисунков или аналитически в виде неравенств или равенств – уравнений связей. Условия, благодаря которым множество точек объединяется в систему, характеризуют внутренние связи. Если на систему не наложены внешние связи, то она называется свободной. Связями (в узком смысле этого термина) называют также материальные тела, создающие ограничения движению изучаемой системы. Пусть механическая система состоит из
♦ В более широком смысле число степеней свободы некоторого детерминистского объекта есть количество параметров, достоверно определяющих данный объект. Так, макросостояние заданного множества молекул, образующих идеальный газ, характеризуется тремя параметрами: температурой, давлением и объемом. Между этими параметрами есть связь, задаваемая объединенным газовым законом, так что число степеней свободы газа равно 2. Если на параметры наложить еще одну связь (напр., пусть давление
В.11. Задание движения механического объекта обычно означает задание кинематическиеуравнений его движения. Кинематические уравнения движения механической системы – это уравнения, выражающие зависимость её обобщенных координат от времени. Количество уравнений движения равно числу степеней свободы объекта. Определим число степеней свободы плоской фигуры (плоского твердого тела, которое может двигаться в неподвижной плоскости). Назначим обобщенные координаты, задающие положение плоской фигуры. Рассмотрим простейшее тело - гантель, состоящую из двух связанных точек
где
а б в Рис.1. Обобщенные координаты плоской фигуры и механизма
Добавление в состав тела следующей точки
Так что независимых уравнений, выражающих внутренние связи (неизменность расстояний между точками плоской фигуры) будет Определим число степеней свободы кривошипа (рис. 1, б) и механизма, называемого шарнирным четырехзвенником (рис. 1, в). Механизмом принято называть искусственно созданную систему тел (звеньев), служащую для преобразования движения одних тел (ведущих звеньев) в требуемые движения других тел (ведомых звеньев). Неподвижное звено механизма называют стойкой. Траектории точек звеньев плоского механизма лежат во взаимно параллельных плоскостях. Кинематическая схема плоского механизма, графически описывающая его структуру и характер движения звеньев, содержит изображения звеньев как плоских фигур. Положение фигуры обычно задают как положение характерного ее отрезка. Два звена, соединенные тем или иным способом друг с другом, образуют кинематическую пару. Звено плоского механизма, образующее со стойкой вращательную пару, называют рычагом или коромыслом. Такое звено способно поворачиваться относительно стойки вокруг неподвижной оси (имеет шарнирное соединение со стойкой). Шарнирные соединения звеньев изображены на рис. 1 маленькими кружками; ось каждого шарнира предполагается проходящей через центр кружка перпендикулярно плоскости рисунка. Рычаг, способный поворачиваться на полный угол, называется кривошипом. Кривошип
Свободной остается координата
Если на механическую систему, имевшую Шарнирный четырехзвенник включает в себя три плоские фигуры: В.12.Сила - величина, характеризующая взаимодействие (взаимовлияние) механических объектов. Сила, действующая на механический объект со стороны другого объекта, - это вектор, имеющий величину, направление и точку приложения. В конкретном взаимодействии участвуют всегда агент и контрагент (см. третий закон Ньютона). В.13. Положение механической системы. Состояние механической системы. Состояниеравновесия механической системы Положение механической системы задается набором значений координат ее точек: Состоянием равновесия механической системы будем называть длящееся некоторое конечное время состояние покоя системы, когда скорости всех ее точек остаются равными нулю. В течение этого времени меры механического движения (количество движения и кинетический момент, а также кинетическая энергия) не изменяются и равны нулю. Положением равновесия называют такое положение механической системы, в котором она способна оставаться бесконечно долго, будучи отпущена из состояния покоя. В.14.Три раздела теоретической механики В разделе «кинематика» исследуется заданное движение механического объекта вне зависимости от сил, действующих на него. В разделе «динамика» исследуется взаимозависимость между силами, действующими на данный объект, и его движением. В разделе «статика» исследуется состояние равновесия объекта в зависимости от действующих на него сил.
КИНЕМАТИКА КИНЕМАТИКА ТОЧКИ 1.1. 1.Способы задания движения точки: векторный, координатный и естественный. 1.1.2. Кинематические параметры точки - это величины, определяющие а) положение (перемещение) точки, б) скорость, в) ускорение точки. Аналогичные кинематические параметры вращающегося твердого тела - это угол его поворота, угловая скорость, угловое ускорение тела.
1.1.3. Траектория точки - геометрическое место положений точки в пространстве, или годограф («рисунок пути») радиус-вектора точки. 1.1.4. Векторперемещения точки Пусть движение точки происходит в интервале времени Вектор перемещения точки за время
Рис. 2. Участок траектории точки
Скорость точки Вектор средней скорости на участке Вектор мгновенной скорости в момент времени
Здесь предыдущая точка Вектор средней скорости Величина скорости (модуль вектора
Ускорение точки Рассмотрим три последовательных положения точки на траектории, соответствующие моментам времени
Вектор среднего ускорения лежит в плоскости треугольника 1.1.7. Путь точки на заданном промежутке времени
1.1.8. Исследовать траекторию точки при координатном способе задания ее движения бывает удобно, если исключить время как параметр из уравнений движения и составить таким способом уравнения траектории в виде зависимостей между координатами точки. 1.1.9. Скорость точки при задании ее движения в декартовой системе координат Проекции скорости на оси координат:
Составляющие скорости по осям координат:
Вектор скорости: Величина (модуль вектора) скорости:
|
||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 442; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.76.43 (0.034 с.) |
 ). Размерность
). Размерность  пространства соответствует действующему в этом пространстве закону обратных квадратов при электростатическом и при гравитационном взаимодействии. Положение точки пространства задается координатами
пространства соответствует действующему в этом пространстве закону обратных квадратов при электростатическом и при гравитационном взаимодействии. Положение точки пространства задается координатами  .
. .
. , где
, где 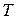 - граница существования условий задачи; если она не установлена, то
- граница существования условий задачи; если она не установлена, то  .
.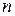 точек, движущихся в пространстве, и пусть связи заданы аналитически в виде
точек, движущихся в пространстве, и пусть связи заданы аналитически в виде  независимых уравнений связей, ограничивающих положения точек системы. Тогда число
независимых уравнений связей, ограничивающих положения точек системы. Тогда число  степеней свободы системы будет равно
степеней свободы системы будет равно .
. ), то число степеней свободы будет равно 1 (изобарный процесс).
), то число степеней свободы будет равно 1 (изобарный процесс). и
и  , движущихся по плоскости в координатной системе
, движущихся по плоскости в координатной системе  (рис.1, а). Расстояние между этим точками (обозначим его
(рис.1, а). Расстояние между этим точками (обозначим его  ) должно быть неизменно (см. п. В.4), т.е. во время движения гантели должно выполняться условие
) должно быть неизменно (см. п. В.4), т.е. во время движения гантели должно выполняться условие ,
, - координаты точек. Это условие дает нам одно уравнение связи, и число степеней свободы гантели как плоского тела, состоящего из
- координаты точек. Это условие дает нам одно уравнение связи, и число степеней свободы гантели как плоского тела, состоящего из  точек, связанных
точек, связанных  уравнением связи, будет равно
уравнением связи, будет равно .
.
 (
( ) не изменит числа степеней свободы: каждая пара «вновь приобретенных» координат
) не изменит числа степеней свободы: каждая пара «вновь приобретенных» координат  связывается двумя уравнениями, выражающими неизменность расстояний
связывается двумя уравнениями, выражающими неизменность расстояний  и
и  :
: .
. . Позиция плоской фигуры вполне определяется положением гантели (или отрезка
. Позиция плоской фигуры вполне определяется положением гантели (или отрезка  ). Положение отрезка зададим координатами
). Положение отрезка зададим координатами  точки
точки 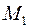 , называемой далее полюсом, и углом
, называемой далее полюсом, и углом  , составляемым вектором
, составляемым вектором  с осью
с осью  . Величины
. Величины  представим как плоскую фигуру, которая при свободном движении по плоскости
представим как плоскую фигуру, которая при свободном движении по плоскости  могла бы иметь
могла бы иметь  степени свободы, но которая имеет неподвижную (общую со стойкой) точку
степени свободы, но которая имеет неподвижную (общую со стойкой) точку  . Последнее условие можно выразить двумя уравнениями связи, задающими координаты полюса
. Последнее условие можно выразить двумя уравнениями связи, задающими координаты полюса  .
. , которую и примем за обобщенную. Число степеней свободы коромысла равно
, которую и примем за обобщенную. Число степеней свободы коромысла равно  .
. степеней свободы, накладываются связи, задаваемые
степеней свободы, накладываются связи, задаваемые  степеней свободы, очевидно, равно
степеней свободы, очевидно, равно  .
. . Условия шарнирных соединений подвижных звеньев со стойкой и друг с другом выражаются восемью уравнениями:
. Условия шарнирных соединений подвижных звеньев со стойкой и друг с другом выражаются восемью уравнениями:  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  . Число степеней свободы механизма
. Число степеней свободы механизма  . Угол
. Угол  есть кинематическое уравнение движения механизма.
есть кинематическое уравнение движения механизма. (или набором обобщенных координат системы
(или набором обобщенных координат системы  ). Состояние системы (фазовое состояние) характеризуется набором координат и совокупностью скоростей её точек
). Состояние системы (фазовое состояние) характеризуется набором координат и совокупностью скоростей её точек  (или обобщенных скоростей
(или обобщенных скоростей  ).
). , и пусть моменту времени
, и пусть моменту времени  соответствует положение
соответствует положение  - положение
- положение  .
. -вектор
-вектор  , имеющий начало в точке
, имеющий начало в точке 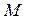 . При векторном задании движения точки вектор перемещения есть «прирост» радиус-вектора точки за время
. При векторном задании движения точки вектор перемещения есть «прирост» радиус-вектора точки за время  :
:

 :
: 

 определена как производная от радиус-вектора слева. Когда последующая точка стягивается к предыдущей точке, то имеем производную справа. Вследствие удара по материальной точке производные от радиус-вектора в момент
определена как производная от радиус-вектора слева. Когда последующая точка стягивается к предыдущей точке, то имеем производную справа. Вследствие удара по материальной точке производные от радиус-вектора в момент  справа и слева могут не совпасть.
справа и слева могут не совпасть. на участке
на участке  на участке
на участке  направлен вдоль секущей
направлен вдоль секущей  ):
): .
. ,
,  ,
,  (рис. 2). Определим среднее ускорение на участке
(рис. 2). Определим среднее ускорение на участке  :
: .
. и лежит в соприкасающейся плоскости. Соприкасающуюся к траектории в точке
и лежит в соприкасающейся плоскости. Соприкасающуюся к траектории в точке  при условии
при условии  , т.е. при
, т.е. при 
 равен длине пройденной ею дуги траектории
равен длине пройденной ею дуги траектории .
.






