
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Молекулярно-кинетическая теория теплоемкости газаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Теплоемкостью какого-либо тела называется величина, равная количеству тепла, которое нужно сообщить телу, чтобы повысить его температуру на один градус. Если сообщение телу количества тепла dQ повышает его температуру на dT, то теплоемкость по определению равна
Величина С имеет размерность [С]=Дж/К. Теплоемкость моля (или киломоля) вещества называется молярной теплоемкостью. Обозначим ее буквой С. Размерность ее [С]=Дж/кмоль×К. Между молярной и удельной теплоемкостями имеется соотношение
Величина теплоемкости зависит от условий, при которых происходит нагревание тела. Наибольший интерес представляет теплоемкость для случаев, когда нагревание происходит при постоянном объеме или при постоянном давлении. Если нагревание происходит при постоянном объеме, тело не совершает работы над внешними телами и, следовательно, согласно первому началу термодинамики dQ = dA + dU, все тепло идет на приращение внутренней энергии dA = 0, dQ = dU. Отсюда вытекает, что теплоемкость любого тела при постоянном объеме равна
Следовательно, чтобы получить молярную теплоемкость идеального газа при постоянном объеме, нужно продифференцировать по температуре выражение для внутренней энергии. Для одного моля газа
Молярная теплоемкость при постоянном объеме
Из этого выражения следует, что теплоемкость идеального газа при постоянном объеме оказывается постоянной величиной, не зависящей от параметров состояния газа, в частности, от температуры. Введя понятие молярной теплоемкости при V=const, можно записать следующее выражение для внутренней энергии идеального газа: U = CVT. Если нагревание газа происходит при постоянном давлении, то газ будет расширяться, совершая над внешними телами положительную работу. Следовательно, для повышения температуры газа на один градус в этом случае понадобится больше тепла, чем при нагревании при постоянном объеме – часть тепла будет затрачиваться на совершение газом работы. Напишем уравнение первого начала термодинамики для моля газа: dQ = dU + dA, учтем, что dA = pdV; dQ = dU + pdV. Разделив на dT, получим выражение для молярной теплоемкости при постоянном давлении:
Слагаемое
Из уравнения Менделеева-Клайперона для одного моля газа следует, что pV = RT. Дифференцируя это выражение по Т, находим, что
Учитывая, что
тогда Cp = CV + R. Для идеального газа молярная теплоемкость при постоянном давлении превышает молярную теплоемкость при постоянном объеме на величину R - универсальную газовую постоянную. Из выражения (8.2) следует, что работа, которую совершает моль идеального газа при повышении его температуры на один градус при постоянном давлении, оказывается равной универсальной газовой постоянной. В этом и заключается ее физический смысл. Так как то Величина отношения
т.е. величина g определяется числом степеней свободы молекул. Рассмотренная теория теплоемкости является классической. Ее результаты приблизительно верны для отдельных температурных интервалов, причем каждому интервалу соответствует свое число степеней свободы молекулы.
различных интервалах теплоемкость имеет значения, соответствующие различному числу степеней свободы молекулы. Так на участке 1-1¢ На участке 2-2¢ В промежутках между указанными интервалами теплоемкость монотонно растет с ростом температуры, т.е. соответствует как бы переменному числу степеней свободы. Объяснение такого поведения дается квантовой механикой. Как устанавливает квантовая теория, энергия вращательного и колебательного движения молекул оказывается квантованной. Это означает, что энергия вращения и энергия колебания молекулы могут иметь не любые значения, а только дискретные (т.е. отдельные, отличающиеся друг от друга на конечную величину) значения. Следовательно, энергия, связанная с этими видами движения, может меняться только скачками. Что и наблюдается на опыте.
8.4. Применение первого начала термодинамики к изопроцессам в газах Изохорный процесс Процесс, протекающий при V=const, называется изохорным. Поскольку при изохорном процессе V=const, а dV=0, то dA=pdV=0, т.е. при изохорном процессе газ работу не совершает. Первое начало термодинамики запишется в этом случае в виде соотношения dU = dQ. Количество теплоты, которое необходимо сообщить системе для того, чтобы при постоянном объеме повысить его температуру на величину dT, можно выразить, если известна теплоемкость вещества при постоянном объеме dQ=CVdT и, следовательно, dU=CVdT. Принимая, что CV - теплоемкость идеального газа не зависит от температуры, для внутренней энергии идеального одноатомного газа получим выражение
Для
Таким образом,
т.е. при изохорном изменении состояния газа вся подведенная к системе теплота идет на увеличение внутренней энергии системы.
Изотермический процесс Процесс, происходящий при постоянной температуре, называется изотермическим процессом. При T = const, U = const, dU = 0. Уравнение первого начала термодинамики при изотермическом состоянии газа запишется в следующей форме: dQ = dA. (8.3) Из этого выражения следует, что при изотермическом процессе все подводимое к системе количество теплоты превращается в работу. Для подсчета работы, совершенной газом при изотермическом расширении от объема V1 до V2, необходимо проинтегрировать выражение для элементарной работы:
Выразив давление из уравнения Менделеева-Клайперона для одного моля газа
и подставив в уравнение для определения работы, получим
Работа, совершаемая при расширении
Графически вычисленная работа (рис.8.6) выражается на диаграмме с координатами pV площадью а bcd, заштрихованной на графике. Вместо отношения
Изобарный процесс Изобарный процесс – процесс, происходящий при постоянном давлении p=const. Работа в этом случае равна
Работа изображается на диаграмме (рис.8.7.) площадью прямо-угольника a bcd.
ного моля газа
для Таким образом, при изобарном процессе подводимое к газу тепло частично тратится на увеличение его внутренней энергии и частично на совершение работы. При изобарном сжатии направление процесса меняется на обратное и работа, совершенная газом становится отрицательной dA<0. Это означает, что не газ совершает внешнюю работу, а внешние силы совершают положительную работу dA по сжатию газа, т.е. dA¢ = dA. Величина dU и dQ при этом также отрицательны, т.е. внутренняя энергия газа уменьшается за счет отдачи им тепла окружающим телам.
Адиабатический процесс Процесс, происходящий без теплообмена с окружающей средой, называется адиабатическим, т.е. в этом случае dQ=0. Уравнение первого начала термодинамики при учете, что dQ = 0 принимает вид dU + dA = 0 или dA = -dU. Т.е. при адиабатическом процессе работа совершается только за счет внутренней энергии газа. При адиабатическом расширении газ совершает работу, а его внутренняя энергия и, следовательно, температура падают. При адиабатическом сжатии работа газа отрицательна (внешняя среда производит работу над газом), внутренняя энергия и температура газа возрастают. Адиабатический процесс можно реализовать и при отсутствии хорошей теплоизоляции. Но тогда необходимо вести процесс столь быстро, чтобы за время его осуществления не произошел существенный теплообмен с окружающей средой. Теплоемкость при адиабатическом процессе
Выведем уравнение кривой, изображающей адиабатический процесс на pV-диаграмме. При бесконечно малом изменении состояния газа совершается работа dA = pdV и изменение внутренней энергии dU = CVdT. Подставив эти значения в уравнение первого начала термодинамики, получим CVdT + pdV = 0. Это и есть уравнение адиабаты в дифференциальной форме. Уравнение содержит все три параметра p,V,T. Для упрощения его воспользуемся уравнением состояния для одного моля газа pV = RT. Дифференцируя его, получим pdV +Vdp = RdT. Составим систему двух уравнений
Умножим первое на R, второе на CV и сложим их: RCVdT + pdVR + pdVCV + VCVdR = CVRdT. Преобразуя выражение, получим (CV + R)pdV + CVVdp = 0. Разделим уравнение на CVpV:
учтем, что CV+R=Cp, т.е. молярной теплоемкоcти при постоянном давлении
Запишем вместо
Левая часть соотношения есть производная от
Отсюда следует, что величина, стоящая в скобках, должна быть постоянной
Учитывая, что pVg = const. (8.4) Это выражение называется уравнением Пуассона или уравнением адиабаты. Его можно записать в ином виде, учитывая, что pV = RT, т.е.
или
уравнений dA = -CVdT; A = -CV(T2-T1); A = CV(T1-T2). 8.6. Круговые, необратимые и обратимые процессы В термодинамических рассуждениях большое значение имеет рассмотрение различных круговых процессов. Круговым процессом и циклом называется такая последовательность превращений, в результате которой система, выйдя из какого-либо исходного состояния, вновь в него возвращается. На диаграмме состояния круговой процесс изображается замкнутой кривой (рис.8.9). Круговой процесс на графике с координатами р и V распадается на два процесса: процесс расширения системы a bc и процесс сжатия cd a. Процесс расширения системы связан с совершением ею работы, в то время как сжатие системы вызывается работой внешних сил.
равная площади фигуры a bcd, соответствует разнице между работой, полученной при расширении системы, и работой, затраченной при возвращении системы в исходное состояние. Различают обратимые и необратимые круговые процессы. Процесс называется обратимым, если система возвращается в исходное состояние, не вызывая изменения в окружающих телах. Чисто механические процессы всегда обратимы. Например, шар, поднятый над землей на высоту h, обладает запасом потенциальной энергии mgh. Cвободно падая, он в конце движения приобретает скорость u, которая может быть найдена из закона сохранения энергии
Ударившись о преграду (удар абсолютно упругий), шар изменит свою скорость на обратную и начнет подниматься. При возвращении шара в исходное положение его потенциальная энергия примет первоначальное значение mgh и, следовательно, во всей системе не произойдет никаких изменений, кроме изменений знака скорости. Процесс обратимый. При наличии теплового движения наблюдаются, как правило, процессы необратимые. Пуля в результате трения о воздух теряет свою скорость, происходит превращение механической энергии в тепловую (пуля и воздух нагреваются). Известно, что повернуть этот процесс так, чтобы рассеянное тепло превратилось опять в энергию механического движения невозможно, т.е. процесс необратим. С практической точки зрения интересны циклические процессы, сопровождающиеся превращением теплоты в работу. Наиболее совершенным в отношении коэффициента полезного действия является циклический процесс, рассмотренный впервые французским физиком Сади Карно и носящий его имя.
Цикл Карно Цикл Карно состоит из двух изотерм (1-2) и (3-4) и двух адиабат (2-3) и (4-1), изображенных на рис.8.10. Для того, чтобы упростить вычисления, предположим, что рассматриваемая система есть один моль идеального газа, хотя полученный вывод будет справедлив для любой системы. Допустим, что начальное (1) состояние системы определяется значением параметров p1V1T1. Предоставим газу возможность расширяться изотермически при температуре Т1 до объема V2. Давление при этом уменьшилось до величины р2 и система придет в состояние (2), характеризуемое p2V2T1. Расширяясь, газ совершает работу
температура газа понизится до величины Т2, а давление до р3. Система перейдет в состояние (3) с параметрами p3V3T2. При этом за счет изменения внутренней энергии будет совершена работа A2-3 = CV (T1 – T2). Для возвращения системы в исходное состояние подвергаем газ, находящийся в результате адиабатного расширения при температуре Т2 изотермическому сжатию до объема V4. Давление при этом возрастает до р4. При этом необходимо совершить работу
Для того, чтобы температура оставалась постоянной, необходимо от газа отвести количество теплоты, эквивалентное затраченной работе Q2=A3-4. Замыкание процесса можно осуществить адиабатическим сжатием газа и его давление принимает первоначальное значение Т1 и р1, и система возвращается в исходное состояние. Сжатие газа при переходе из состояния (4®1) потребует затраты работы, эквивалентной возрастанию внутренней энергии системы A4-1 = CV (T1 – T2). Работа, совершенная системой при расширении, равна сумме
Работа, затраченная на возвращение системы в исходное состояние, равна сумме
Их разность является полезной во всем цикле
Для характеристики эффективности циклического процесса в отношении превращения теплоты в работу, вводится физическая величина, называемая коэффициентом полезного действия цикла. Коэффициент полезного действия цикла (h) равен отношению работы Аполезн=А1-2-А3-4, практически используемой в данном цикле, к работе, которую можно было бы получить при превращении в нее всего количества тепла, подведенного к системе
или, учитывая эквивалентность теплоты и работы,
Подставляя (8.5) и (8.6) в формулу (8.7), получим
Для того, чтобы упростить это выражение, заметим, что объемы V2 и V3, так же как объемы V4 и V1, лежат попарно на соответствующих адиабатах и поэтому, согласно уравнению Пуассона, для них справедливы следующие соотношения:
Извлекая корень (g-1) степени, находим, что
Таким образом, коэффициент полезного действия цикла Карно равен отношению разности между абсолютной температурой Т1, при которой происходит изотермическое расширение газа, и абсолютной температурой изотермического сжатия газа Т2 к абсолютной температуре расширения газа Т1. Подобные круговые процессы могут лежать в основе действия как тепловой машины, так и холодильной машины.
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 1774; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.106.207 (0.009 с.) |

 .
. .
. .
. .
. .
. ,
,  .
.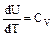 - молярная теплоемкость при постоянном объеме, поэтому
- молярная теплоемкость при постоянном объеме, поэтому .
. .
. , получим
, получим , (8.2)
, (8.2) .
.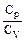 , обозначаемая g, называется коэффициентом Пуассона:
, обозначаемая g, называется коэффициентом Пуассона: ,
, CV
7/2R 3 3¢
2 2¢
5/2R
1 1¢
3/2R
0 T
Рис.8.5
CV
7/2R 3 3¢
2 2¢
5/2R
1 1¢
3/2R
0 T
Рис.8.5
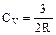 . Это означает, что молекула ведет себя как cистема, обладающая только поступательными степенями свободы.
. Это означает, что молекула ведет себя как cистема, обладающая только поступательными степенями свободы. , следовательно, при температурах, соответствующих этому участку, у молекулы, в дополнение к проявляющимся при более низких температурах, трем поступательным степеням свободы, добавляются еще две – вращательные. Наконец, при достаточно больших температурах
, следовательно, при температурах, соответствующих этому участку, у молекулы, в дополнение к проявляющимся при более низких температурах, трем поступательным степеням свободы, добавляются еще две – вращательные. Наконец, при достаточно больших температурах  , что свидетельствует о наличии при этих температурах колебаний молекулы.
, что свидетельствует о наличии при этих температурах колебаний молекулы.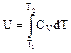 .
. киломолей
киломолей .
. ,
, .
.
 ,
,  .
. .
. , можно воспользоваться равным ему обратным отношением давлений, исходя из закона Бойля-Мариотта, тогда
, можно воспользоваться равным ему обратным отношением давлений, исходя из закона Бойля-Мариотта, тогда .
Согласно (8.3), при T=const Q=A, т.е.
.
Согласно (8.3), при T=const Q=A, т.е.
 .
.
 p
a
b
d c
V1 V2 V
Рис.8.6
p
a
b
d c
V1 V2 V
Рис.8.6
 .
. a b
d c
V1 V2 V
Рис.8.7
a b
d c
V1 V2 V
Рис.8.7
 ,
, .
. .
.
 ,
, .
.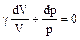 .
. , поэтому
, поэтому .
. .
. и потенцируя выражение, получим
и потенцируя выражение, получим
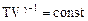 .
.
 p
a
b
d
c
k e V
Рис.8.9
p
a
b
d
c
k e V
Рис.8.9
 .
. . (8.5)
. (8.5) p
p1V1T1
1 p2V2T1
4 p3V3T2
p4V4T2 3
V
Рис.8.10
p
p1V1T1
1 p2V2T1
4 p3V3T2
p4V4T2 3
V
Рис.8.10
 .
. .
. .
. . (8.6)
. (8.6) (8.7)
(8.7)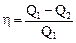 .
. . (8.8)
. (8.8) ;
; ;
;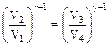 .
. . Учитывая это, равенство (8.8) можно переписать в виде
. Учитывая это, равенство (8.8) можно переписать в виде .
.


