
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основное уравнение молекулярно-кинетической теории газовСодержание книги
Поиск на нашем сайте При ударе о стенку сосуда молекула сообщает ей импульс, численно равный изменению количества движения молекулы. Каждый элемент поверхности стенки Ds непрерывно подвергается бомбардировке большим количеством молекул, в результате чего за время Dt получает суммарный импульс, направленный по нормали к Ds. Отношение импульса к Dt, как известно, есть сила, действующая на Ds и есть давление. Для получения этого давления введем два упрощения, касающиеся характера движения молекул.
них, т.е. Второе упрощение состоит в том, что всем молекулам мы придадим одинаковое значение скорости. Вычислим импульс, сообщаемый стенке сосуда, ударяющейся об него молекулой. До удара о стенку количество движения молекулы направлено по внешней нормали к Ds и равно mu (рис.7.2). В результате удара количество движения меняет знак. Таким образом, приращение количества движения молекулы равно (-mu) - (mu) = -2mu. По третьему закону Ньютона стенка получит при ударе импульс 2mu, имеющий направление нормали.
ки Ds долетят все движущиеся по направлению к нему молекулы, заключенные в объеме цилиндра с основанием Ds и высотой uDt. Число этих молекул равно
где n - число молекул в единице объема. Число ударов молекул о площадку Ds за единицу времени будет равно
Умножим число ударов на импульс, сообщаемый стенке при каждом ударе, получим суммарный импульс, сообщаемый элементу стенки за время Dt,
т.е.
Разделив эту величину на Ds и Dt, получим давление газа, оказываемое на стенки сосуда
Учитывая, что
Если в выводе учесть, что скорости отдельных молекул ui будут различны, то величину nu2 следует заменить суммой квадратов ско- ростей каждой из молекул, находящихся в единице объема
Отсюда видно, что в (7.1) следует заменить u2 на
где средняя кинетическая энергия поступательного движения молекулы
Соотношение
называется основным уравнением молекулярно-кинетической теории (МКТ) идеального газа.
|
||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 421; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.006 с.) |

 молекул, причем половина из
молекул, причем половина из



 , движется вдоль данного направления в одну сторону, половина – в противоположную сторону (рис.7.1). Основываясь на таком предположении, мы будем считать, что в интересующем нас направлении движется
, движется вдоль данного направления в одну сторону, половина – в противоположную сторону (рис.7.1). Основываясь на таком предположении, мы будем считать, что в интересующем нас направлении движется  часть молекул.
часть молекул. -mu
mu
-mu
mu  Ds
Рис.7.2
Ds
Рис.7.2
 ,
, .
. ,
, .
. . (7.1)
. (7.1)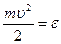 - кинетическая энергия поступательного движения молекулы, предыдущее выражение можно записать в виде
- кинетическая энергия поступательного движения молекулы, предыдущее выражение можно записать в виде . (7.2)
. (7.2) .
. , так как
, так как  - средний квадрат скорости, и переписать уравнение (7.2) в виде
- средний квадрат скорости, и переписать уравнение (7.2) в виде ,
, .
.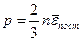 . (7.3)
. (7.3)


