
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Больцмановское распределение частиц в потенциальном поле. Закон максвелла-больцманаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Если в барометрическую формулу (7.26) подставить основное уравнение молекулярно-кинетической теории газов в виде p=nkT, то получим закон изменения с высотой числа молекул в единице объема:
где n0 - число молекул в единице объема на высоте, равной нулю, n - то же число на высоте h. Величина
2) тепловое движение, характеризуемое величиной kT, стремится разбросать молекулы равномерно по поверхности Земли. Чем больше m и меньше Т, тем сильнее преобладает первая тенденция, и молекулы сгущаются у поверхности Земли. При высоких температурах преобладает тепловое движение и плотность молекул медленно убывает с высотой. На разной высоте молекула обладает различным запасом потенциальной энергии ep = mgh. (7.28) Следовательно, распределение молекул по высоте является вместе с тем и распределением их по значениям потенциальной энергии. Подставляя (7.28) в (7.27), получим распределение Больцмана в виде
где n0 - число молекул в единице объема, в том месте, где ep=0, n - число молекул, где потенциальная энергия молекулы равна ep. Выражение (7.29) показывает, что молекулы располагаются с большей плотностью там, где меньше их потенциальная энергия и, наоборот, с меньшей плотностью в местах, где их потенциальная энергия больше. Если взять отношения n1 и n2 в точках, где потенциальная энергия молекулы имеет значение
Больцман показал, что распределение (7.29) и вытекающее из него выражение (7.30) справедливо не только в случае потенциального поля сил земного тяготения, но и в любом потенциальном поле сил для совокупности любых одинаковых частиц, находящихся в состоянии хаотического теплового движения. Таким образом, закон Максвелла дает распределение частиц по значениям кинетической энергии, закон Больцмана дает распределение частиц по значениям потенциальной энергии. Для обоих распределений характерно наличие экспоненциального множителя, в показателе которого стоит отношение кинетической или соответственно потенциальной энергии одной молекулы к величине, определяющей среднюю энергию теплового движения молекул. Эти два распределения можно объединить в один закон Максвелла-Больцмана. Согласно распределению Максвелла, количество молекул, содержащихся в единице объема, скорость которых лежит между u и u+du равно dn = n×f(u)du, (7.31) где
Подставляя (7.29) и (7.32) в (7.31), получим закон Максвелла-Больцмана
или где Е - полная энергия молекулы.
7.8. Экспериментальный метод определения числа Авогадро В газе, находящемся в поле силы тяжести, число молекул в единице объема убывает с высотой. Если число молекул в единице объема на нулевой высоте равно n0, то на высоте h оно равно
где m - масса молекулы, g - ускорение силы тяжести, k - постоянная Больцмана, Т – температура по шкале Кельвина. Эта формула была применена Перреном для броуновских частиц и использована для определения числа Авогадро. Взвешенные в жидкости, очень мелкие твердые частицы, находящиеся в состоянии непрерывного беспорядочного движения, называются броуновскими частицами. Принимая участие в тепловом движении, эти частицы должны вести себя подобно гигантским молекулам и для них должны выполняться закономерности кинетической теории, в частности, закон (7.33). Во время опыта по определению числа Авогадро была взята стеклянная трубка с эмульсией глубиной 0,1 мм и помещена под микроскоп. Микроскоп имел столь малую глубину поля зрения, что в него были видны только частицы, находящиеся в горизонтальном слое толщиной примерно один микрон. Перемещая микроскоп в вертикальном направлении, можно было исследовать распределение броуновских частиц по высоте. Обозначим высоту слоя, видимого в микроскоп над дном кюветы буквой h. Число частиц, попадающих в поле зрения микроскопа, определяется формулой DN = n(h)sDh, где n(h) – число броуновских частиц в единице объема на высоте h, s - площадь, Dh - глубина поля зрения микроскопа. Согласно формулы (7.33), можно записать для броуновских частиц, что
где mg - сила тяжести броуновской частицы в эмульсии, взятая с учетом закона Архимеда. Запишем выражение числа частиц Dh для двух разных высот h1 и h2 и получим
Возьмем отношение этих двух величин и, прологарифмировав данное выражение, получим
Измеряя mg, Т, (h2-h1), DN1 и DN2, можно определить постоянную Больцмана:
Число Авогадро связано с k соотношением
Исходя из данных этого эксперимента, Перрен получил значение NA в пределах от 6,5×1026 до 7,2×1026 кмоль-1. Определенное другими, более точными методами, значение NA = 6,02×1026 кмоль-1. Таким образом, значение, полученное Перреном, находится в хорошем согласии со значениями, полученными другими методами, что доказывает применимость к броуновским частицам закона распределения Больцмана.
|
||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 761; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.171.121 (0.006 с.) |

 ,
,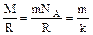 , где m - масса одной молекулы, NA - число Авогадро, k - постоянная Больцмана. Следовательно,
, где m - масса одной молекулы, NA - число Авогадро, k - постоянная Больцмана. Следовательно, . (7.27)
. (7.27) T2>T1
T1
T2
h
Рис.7.10
T2>T1
T1
T2
h
Рис.7.10
 , (7.29)
, (7.29) и
и  , то
, то . (7.30)
. (7.30) . (7.32)
. (7.32)
 ,
, , (7.33)
, (7.33) ,
, ,
, .
. .
. .
.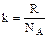 , откуда
, откуда  , где R - универсальная газовая постоянная, т.е.
, где R - универсальная газовая постоянная, т.е.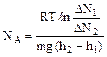 .
.


