
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Распределение молекул по скоростям. Закон максвеллаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Предположим, что мы располагаем способом одновременного определения скоростей N-молекул некоторого количества газа. Изобразим полученные результаты в виде точек на оси u. При этом мы получим «моментальную фотографию» скоростей молекул для некоторого момента времени t. Если бы все значения были одинаково вероятны, точки распределялись бы по оси равномерно (рис.7.3)
Однако скорости группируются в основном вблизи некоторого, наиболее вероятного значения. Близкие к нулю и очень большие значения скоростей встречаются сравнительно редко. Поэтому распределение точек по оси u будет неравномерным с плотностью, различной на разных участках оси (рис.7.4).
Отношение числа точек DNu, попадающих в пределах интервала Du, к величине этого интервала, называется плотностью точек (r):
Если сопоставить ряд фотографий для разных моментов времени, то плотность будет различна. Для газа, находящегося в равновесном состоянии, т.е. для газа с неизменяющимися параметрами, плотность, с которой распределены точки на различных участках оси u для всех моментов времени будет одна и та же. Если взять несколько порций газа, находящегося в идентичных условиях, то распределение молекул по скоростям будет также идентично. Однако плотность точек по оси u при одинаковом характере распределения по оси, очевидно, пропорциональна количеству молекул N и, следовательно, для различных порций газа будет различна. Одинаковым для различных порций будет соотношение
Определенная таким образом функция f(u) характеризует распределение молекул газа по скоростям и называется функцией распределения, где DNu = Df(u)Du - число молекул, скорость которых больше u, но меньше u+Du;
Попытаемся найти аналитическое выражение закона распределения молекулярных скоростей. Скорость каждой молекулы изображается вектором. В прямоугольной системе координат вектор скорости u определяется координатами ux, uy, uz (рис.7.5). Очевидно, что эти координаты одновременно будут являться компонентами скорости вдоль выбранных осей координат. Тогда число молекул
вдоль оси y, большей uy и меньшей uy+Duy:
Вероятность составляющей скорости вдоль оси z, заключенной в пределах от uz до uz+Duz:
Из теории вероятности известно, что вероятность совместного осуществления трех независимых событий равна произведению их вероятностей. Поэтому вероятность
Допустим, что нижний предел скорости u=const, в этом случае
uxDux+uyDuy+uzDuz = 0. Допустим также, что DuxDuyDuz = const. При выполнении этих предположений должна оставаться неизменной и вероятность
Подставив в равенство (7.17) равенство (7.16) и учитывая (7.18), получим
Разделим полученное уравнение на произведение функций f(ux)f(uy)f(uz), получим
Умножим выражение (7.17) на произвольную величину l, сложим с уравнением (7.19), сгруппируем члены в соответствии с индексами у u и получим
В силу произвольности величин dux, duy, duz написанное уравнение может выполняться в том случае, если каждый из стоящих в скобках двучленов порознь равен нулю, т.е.
Обозначим f(ux,)=y, тогда
После интегрирования
имеем
где А – постоянная интегрирования. Потенцируя данное выражение, получим
Таким образом, искомое выражение вероятности
Аналогичные выражения можно получить из (7.21) для вероятности того, что скорость молекулы вдоль оси y заключена в пределах от uy до uy+Duy и из (7.22) для вероятности того, что скорость молекулы в направлении оси z заключена в пределах от uz до uz+Duz. Вероятность совместного события найдется перемножением соответствующих вероятностей, т.е.
Если в этом выражении заменить
где m - масса, k - постоянная Больцмана, Т – абсолютная температура. Учитывая, что
Это выражение и является искомым законом распределения молекулярных скоростей Максвелла. Таким образом, конкретный вид функции распределения зависит от рода газа (массы молекул) и от температуры. Давление газа и объем на распределение молекул по скоростям не влияют. Графическое изображение закона распределения Максвелла, представленном на рис.7.6.
Для нахождения максимума функции f(u) продифференцируем выражение (7.24), заменяя через
и, приравняв к нулю получим
Значение u, обращающее в нуль выражение, стоящее в скобках, представляет собой искомое uвер:
Вычисления показывают, что
поэтому При возрастании температуры средняя скорость Закон справедлив для любого числа Закон Максвелла – статистический закон, а законы статистики выполняются тем точнее, чем к большему числу одинаковых объектов они применяются. При малом числе объектов могут наблюдаться значительные отклонения от предсказаний статистики.
рость которых лежит в любом определенном интервале скоростей Du, не меняется. Если в результате столкновений в единицу времени Dn молекул, обладавших скоростью в интервале Du, изменяют свою скорость, то ровно столько же молекул, обладавших ранее другими скоростями, приобретут в результате столкновений скорость в пределах Du. Раз установившееся максвелловское распределение по скоростям в дальнейшем сохраняется. Более того, как показал Больцман, в результате взаимодействия между молекулами, каким бы ни было исходное распределение скоростей, в конце концов (весьма быстро) устанавливается максвелловское распределение.
Барометрическая формула. Действие силы тяжести приводит к определенному распределению молекулярной плотности по высоте газового столба. Одновременно с изменением плотности изменяется и давление, измеряемое барометром. Пусть имеется свободный столб газа, поддерживаемый при постоянной температуре. Выделим мысленно столб газа с основанием 1 см2 (рис.7.8). Обозначим р0 давление газа у основании столба, р – давление газа на высоте h. Тогда давление газа на высоте h+dh равно p+dp. Причем, давление во втором сечении будет меньше, чем в первом на величину p+dp.
Отсюда dp = -rgdh. (7.24) Из уравнения Менделеева-Клайперона следует, что
где V - объем газа, М – молярная масса газа, m - масса газа. Заменим в данном уравнении
Подставим (7.25) в (7.24):
разделим переменные и проинтегрируем полученное выражение:
Потенцируя последнее уравнение, найдем зависимость давления от высоты при сделанном нами допущении о постоянстве температуры:
Эта формула называется барометрической.
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 590; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.009 с.) |

 O x x x x x x x x x x x u
Рис.7.3
O x x x x x x x x x x x u
Рис.7.3
 O x x x x x x x x x x x u
Du
Рис.7.4
O x x x x x x x x x x x u
Du
Рис.7.4
 .
. . (7.12)
. (7.12) есть вероятность того, что скорость молекулы будет иметь значение в пределах данного интервала скоростей.
есть вероятность того, что скорость молекулы будет иметь значение в пределах данного интервала скоростей. , составляющие скорости которых больше ux, но меньше ux+Dux согласно равенству (7.12), равны
, составляющие скорости которых больше ux, но меньше ux+Dux согласно равенству (7.12), равны . (7.13)
. (7.13) есть вероятность для произ-вольно выбранной молекулы обладать скоростью, лежащей в указанном интервале.
Рассуждая аналогично, можно написать выражение вероятности для молекул обладать составляющей скорости
есть вероятность для произ-вольно выбранной молекулы обладать скоростью, лежащей в указанном интервале.
Рассуждая аналогично, можно написать выражение вероятности для молекул обладать составляющей скорости
 z
z
 uz
ux x
uy
y
Рис.7.5
uz
ux x
uy
y
Рис.7.5
 . (7.14)
. (7.14) . (7.15)
. (7.15) для молекулы обладать скоростью, компоненты которой заключены в пределах от ux, uy, uz, до (ux+Dux), (uy+Duy), (uz+Duz) найдется перемножением 3-х вероятностей (7.13), (7.14) и (7.15):
для молекулы обладать скоростью, компоненты которой заключены в пределах от ux, uy, uz, до (ux+Dux), (uy+Duy), (uz+Duz) найдется перемножением 3-х вероятностей (7.13), (7.14) и (7.15): . (7.16)
. (7.16) ;
; того, что молекула обладает скоростью, удовлетворяющей сформулированным выше требованиям. Если это так, то
того, что молекула обладает скоростью, удовлетворяющей сформулированным выше требованиям. Если это так, то , (7.17)
, (7.17)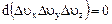 . (7.18)
. (7.18)
 . (7.19)
. (7.19) .
. ; (7.20)
; (7.20) ; (7.21)
; (7.21)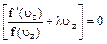 . (7.22)
. (7.22) и (7.20) перепишется в виде
и (7.20) перепишется в виде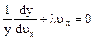 .
.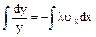
 ,
, .
. того, что скорость молекулы в направлении оси x, заключенной в пределах от ux до ux+Dux будет равна
того, что скорость молекулы в направлении оси x, заключенной в пределах от ux до ux+Dux будет равна .
. .
. и определить значение постоянных, то вероятность того, что молекула движется независимо от направления со скоростью, заключенной в пределах от u до u+Du, будет выражаться следующим соотношением
и определить значение постоянных, то вероятность того, что молекула движется независимо от направления со скоростью, заключенной в пределах от u до u+Du, будет выражаться следующим соотношением , (7.23)
, (7.23) , из (7.23) получим
, из (7.23) получим . (7.24)
. (7.24) f(u)
u
u u+Du uвер
f(u)
u
u u+Du uвер 
 Рис.7.6
Рис.7.6
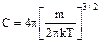 :
: ;
;
 ,
, .
. .
.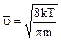 ,
,  ,
, .
. и наиболее вероятная скорость uвер увеличиваются пропорционально
и наиболее вероятная скорость uвер увеличиваются пропорционально  , и максимум распределения сдвигается вправо (рис.7.7). При этом число медленных молекул убывает, а число быстрых – возрастает. Но площадь под кривой, равная полному числу всех молекул газа
, и максимум распределения сдвигается вправо (рис.7.7). При этом число медленных молекул убывает, а число быстрых – возрастает. Но площадь под кривой, равная полному числу всех молекул газа  , остается постоянной. Необходимо подчеркнуть, что установленный Максвеллом закон распределения молекул по скоростям и все вытекающие из него следствия, справедливы только для газа, находящегося в равновесном состоянии.
, остается постоянной. Необходимо подчеркнуть, что установленный Максвеллом закон распределения молекул по скоростям и все вытекающие из него следствия, справедливы только для газа, находящегося в равновесном состоянии. f(u)
T2>T1
T1
T2
0 u
Рис.7.7
f(u)
T2>T1
T1
T2
0 u
Рис.7.7

 ,
, через r - плотность газа:
через r - плотность газа: . (7.25)
. (7.25) ,
, ;
; ;
; .
. . (7.26)
. (7.26) p M1< M2
T1 > T2
M1(T1)
M2(T2)
h
Рис.7.9
p M1< M2
T1 > T2
M1(T1)
M2(T2)
h
Рис.7.9



