
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Эффективный диаметр молекулы. Число столкновений и средняя длина свободного пробега молекулыСодержание книги
Поиск на нашем сайте
Молекулы газа, находясь в тепловом движении, непрерывно сталкиваются друг с другом. Минимальное расстояние, на которое сближаются при столкновении центры двух молекул, называется эффективным диаметром молекулы d (рис.7.11). Путь, который проходит молекула за время между двумя последовательными соударениями, называется длиной свободного пробега
где z - число соударений. Число свободных пробегов за какой-то промежуток времени совпадает с числом соударений молекулы за тоже время. Если за 1 с молекула испытала z соударений, то длина ее траектории, численно равная средней скорости ее движения, будет состоять из z свободных пробегов. Отношение средней скорости движения молекулы к средней длине свободного пробега определяет среднее число соударений.
Для вычисления средней длины свободного пробега молекулы предположим, что все молекулы газа, за исключением одной, неподвижны и распределены равномерно по всему объему. Будем считать, что скорость движущейся молекулы совпадает со средней скоростью молекулярного движения идеального газа. Двигаясь, молекула соударяется с другими всякий раз, когда она приближается к ним настолько, что расстояние между их центрами делается равным эффективному диаметру молекулы (рис.7.12).
Если молекула движется в течение 1 с, то высота этого цилиндра равна средней скорости молекулы
Очевидно, что соударения будут происходить всякий раз, когда центр встречной молекулы будет находиться вблизи цилиндра, вырезанного сферой ограждения. Следовательно, для определения среднего числа соударений Таким образом, среднее число соударений молекулы за одну секунду равно
При получении этого соотношения все молекулы газа, кроме одной, считались неподвижными. Более строгая теория показывает, что при учете движения всех молекул и при условии, что скорости молекулярного движения распределены согласно закону Максвелла, среднее число соударений молекулы за 1 с будет несколько больше и может быть подсчитано по уравнению
Зная среднее число соударений молекулы, можно определить среднюю длину пробега молекулы:
где n0 - число молекул газа в единице объема. Из основного уравнения молекулярно-кинетической теории
подставив (7.35) в (7.34), получим
Таким образом, при постоянной температуре средний свободный пробег молекулы обратно пропорционален давлению. При повышении температуры средняя длина пробега несколько растет. Зависимость
где С – характерная для каждого газа постоянная величина, имеющая размерность температуры и носящая название постоянной Сёзерленда,
Явления переноса в газах До сих пор мы рассматривали газ, находящийся в равновесном состоянии. Такое состояние газа характеризуется тем, что параметры газа (объем, давление, температура) не изменяются. Теперь рассмотрим явления, возникающие при отклонении газа от равновесия, причем ограничимся случаями, когда отклонения невелики. Подобные явления называются явлениями переноса. Мы рассмотрим три таких явления: 1) внутреннее трение или вязкость; 2) теплопроводность; 3) диффузию.
|
||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 694; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.006 с.) |

 .
. d
Рис.7.11
d
Рис.7.11
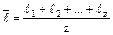 ,
, .
. d
Рис.7.12
d
Рис.7.12
 , а объем, вырезанный сферой ограждения, составляет
, а объем, вырезанный сферой ограждения, составляет .
. достаточно подсчитать число молекул газа, центры которых находятся вблизи указанного цилиндра. Это число равно произведению объема цилиндра V на количество молекул газа в единице объема n0.
достаточно подсчитать число молекул газа, центры которых находятся вблизи указанного цилиндра. Это число равно произведению объема цилиндра V на количество молекул газа в единице объема n0. .
. .
. , (7.34)
, (7.34) , (7.35)
, (7.35) .
. от Т дается формулой Сёзерленда
от Т дается формулой Сёзерленда ,
, - средняя длина свободного пробега при Т® ¥.
- средняя длина свободного пробега при Т® ¥.


