
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Средняя кинетическая энергия молекул. Молекулярно-кинетическое толкование абсолютной температуры. Связь основного уравнения МКТ с уравнением Менделеева-КлайперонаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Число молекул в единице объема n можно заменить отношением полного числа всех молекул газа N, находящихся в сосуде, к его объему V, т.е.
Из определения средней энергии поступательного движения молекул и средней квадратичной скорости следует, что
где
Следовательно, произведение объема газа на его давление численно равно 2/3 кинетической энергии хаотического поступательного движения всех молекул газа, заключенных в этом объеме. Это соотношение связывает макроскопические наблюдаемые и измеряемые величины р и V с основной характеристикой
Поскольку в знаменателе стоит объем, занимаемый газом, то, очевидно, что вся дробь будет представлять кинетическую энергию молекул в единице объема, т.е. давление газа измеряется плотностью кинетической энергии движущихся молекул газа. Подставляя произведение давления на объем из уравнения Менделеева-Клайперона
в выражение (7.4), получим
Таким образом, энергия идеального газа прямо пропорциональна его абсолютной температуре. Под Средняя кинетическая энергия поступательного движения одной молекулы равна полной энергии газа, деленной на число молекул. Число молекул, содержащихся в
где NA - число Авогадро. Разделив (7.5) на (7.6), получим среднюю кинетическую энергию одной молекулы:
Величины R и Na являются универсальными постоянными. Их отношение Введя постоянную Больцмана, мы можем переписать выражение для средней кинетической энергии одной молекулы в виде
Таким образом, средняя кинетическая энергия хаотического движения молекул идеального газа прямо пропорциональна его абсолютной температуре и является мерой интенсивности теплового движения молекул при заданной температуре. Это формула позволяет выявить молекулярно-кинетический смысл температуры.
Температура тела есть количественная мера энергии теплового движения молекул, из которых состоит тело. Из выражения (7.7) следует, что при одинаковой температуре средние кинетические энергии молекул всех газов одинаковы, несмотря на различие масс молекул разных газов. Подставляя в (7.7) (7.3), можно преобразовать основное уравнение кинетической энергии газов к виду p = nkT. (7.8) где р – давление газа, n – концентрация молекул, Т – абсолютная температура, k - постоянная Больцмана.
|
|||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 917; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.218.118 (0.007 с.) |

 , и уравнение (7.3) переписать в виде
, и уравнение (7.3) переписать в виде .
. ,
, - суммарная кинетическая энергия поступательного движе-ния всех молекул газа, и уравнение (7.3) можно переписать в виде
- суммарная кинетическая энергия поступательного движе-ния всех молекул газа, и уравнение (7.3) можно переписать в виде . (7.4)
. (7.4) .
.
 . (7.5)
. (7.5) молей равно
молей равно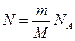 , (7.6)
, (7.6) .
. также является универсальной постоянной и носит название постоянной Больцмана, равной k=1,38×10-23 Дж/к.
также является универсальной постоянной и носит название постоянной Больцмана, равной k=1,38×10-23 Дж/к. . (7.7)
. (7.7)


