
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства потенциала действияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Благодаря теории ионного возбуждения Ходжкина — Хаксли, что является существенным доказательством ее правильности, стало возможным объяснить с помощью основных ее положений свойства потенциала действия, а также механизмы его распространения в нервных и мышечных клетках. Аккомодация. Закон раздражения Дюбуа-Реймона. Как было выяснено, для того чтобы возник потенциал действия, необходимо деполяризовать мембрану до порогового значения. Однако ни пороговый раздражающий ток, ни пороговый потенциал не имеют определенной величины, поскольку зависят от нескольких факторов, в том числе и от скорости деполяризации мембраны. Зависимость порога возникновения потенциала действия от скорости нарастания раздражающего тока получила название закона раздражения Дюбу а-Р е й м о н а, суть которого состоит в том, что для достижения порога раздражения сила тока должна нарастать с определенной скоростью. При медленном нарастании силы тока возбуждение не наступает (рис. 2.13). Это явление, названное аккомодацией, связано со свойствами инактивации (закрывания) натриевых каналов и активации калиевых каналов при длительной деполяризации. В частности, повышение мембранного потенциала к пороговому уровню вызывает открывание натриевых каналов и соответственно возникновение входящего, натриевого тока. Однако, если скорость этого процесса недостаточна, часть натриевых каналов успевает закрыться. В то же время при деполяризации происходит активация калиевых кана-
лов, у которых в отличие от натриевых инактивация не происходит. Таким образом, ослабляется входящий натриевый ток и усиливается выходящий калиевый ток. Все это замедляет или блокирует развитие регенеративного процесса.
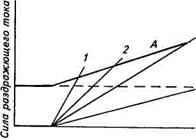
Закон длительности раздражения. Закон Дюбуа-Реймона тесно связан с другим необходимым условием наступления возбуждения — определенной длительности раздражения. Исследованию данной проблемы были посвящены многочисленные работы, начатые еще в конце XIX в., экспериментальные данные которых позволили сделать вывод, что порог возбуждения не может быть достигнут, если раздражение длится очень долго, но сила его мала, или сила раздражения велика, но действует очень короткий промежуток времени. Кривая, выражающая зависимость необходимой силы тока от времени раздражения нервного волокна, имеет вид гиперболы и никогда полностью не приближается к осям координат (рис. 2.14). Начиная с некоторого момента кривая идет параллельно оси абсцисс — оси времени, т. е. сила ниже порого- О 0,2 0,4 0,6 0,8 1,0 1,2 1,4 1,6 1,8 2,0 2,2 2,4 2,6 Длительность, мс Рис. 2.14. Кривая «сила — длительность» для возникновения потенциала в нерве: /: по оси ординат — реобаза, по оси абсцисс — полезное время; //: по оси ординат — двойная реобаза, по оси абсцисс — хронаксия вой не вызывает возбуждения ни при какой длительности раздражения — время бесполезно. И наоборот, начиная с пороговой силы, время становится значимым (полезным) для раздражения. По существу, «полезное время» — это критическая длительность действия наименьшего тока, способного вызвать возбуждение. Применимо к нервной или мышечной клетке это возникновение потенциала действия. Для того чтобы импульс тока мог изменить мембранный потенциал и вызвать потенциал действия, через мембрану должно пройти некоторое минимальное количество электричества Q, которое, как известно, измеряется как произведение силы тока /на время t: Q = It. Из соотношения следует, что по мере сокращения длительности тока необходимо увеличить его силу, чтобы он сохранял эффективность в качестве раздражителя. Для импульсов большой длительности существует некоторая минимальная сила тока, достаточная для возбуждения. Более слабый ток из-за того что мембрана в покое имеет определенную проводимость для ионов калия, не способен вызвать необходимое смещение трансмембранной разности потенциалов и запустить регенеративный процесс генерации потенциала действия. Таким образом, «полезное время» может свидетельствовать об уровне возбудимости ткани: чем короче «полезное время», тем более возбудимыми являются ткани и быстрее реагируют на раздражитель. Это положение с начала XX в. успешно используется в клинической и лабораторной практике. Вместе с тем следует, что точное измерение «полезного времени» затруднительно, поскольку в этой части кривой значительные изменения времени соответствуют очень малым изменениям порога раздражения (см. рис. 2.14). Поэтому французским исследователем Лапиком было предложено измерять в качестве порога времени минимальную длительность раздражителя при его силе, равной двум порогам, и при условии, что сила порогового раздражителя измерена при длительностях, превышающих «полезное время». Временные интервалы и значения силы раздражителя получили специальные названия и используются по настоящее время. Пороговая сила была обозначена как реобаза, а необходимое время раздражения при силе раздражения, равной двум реобазам, — хронаксия. Хронаксия — величина переменная и зависит от многих факторов: структуры ткани, ее функционального состояния и всего организма в целом. Кривые «сила — длительность» для разных тканей и органов подобны по форме, но отличаются во времени. Например, у лошади и жвачных животных хронаксия двигательных нервов колеблется от 0,09 до 0,2 мс, а скелетных мышц — от 0,2 до 0,4 мс; самая большая хронаксия у гладких мышц желудка, кишечника и матки, измеряемая десятками и сотнями миллисекунд. Рефрактерность. После окончания возбуждения в нервных или мышечных клетках или, другими словами, после окончания в них потенциала действия наступает состояние временной невозбуди-
Рис. 2.15. Периоды рефрактерности (снижения возбудимости) при генерации потенциала действия: верхняя запись — потенциалы действия, генерируемые на электрическое раздражение, нижняя запись — отметка электрического раздражения; А — период абсолютной рефрактерности; Б— период относительной рефрактерности; 1...4— периоды рефрактерности
Наличие периодов абсолютной и относительной рефрактерности легко объяснимо на основании данных о динамике активации и инактивации натриевых и калиевых ионных каналов во время генерации потенциала действия. Так, в период абсолютной рефрактерности во время нисходящей части потенциала действия повышается калиевая проводимость за счет открывания дополнительных калиевых каналов и снижается натриевая проводимость за счет инактивации натриевых каналов. Поэтому даже при больших значениях деполяризующего тока не удается активировать такое число натриевых каналов, чтобы выходящий натриевый ток мог бы превысить увеличенный выходящий калиевый ток и снова запустить регенеративный процесс. Во время относительного рефрактерного периода деполяризующий сигнал достаточно большой амплитуды может активировать воротный механизм натриевых каналов так, что, несмотря на большое число открытых калиевых каналов, натриевая проводимость увеличивается и вновь возникает потенциал действия. Вместе с тем из-за увеличенной проводимости мембраны к ионам калия и остаточной натриевой инактивации повышение мембранного потенциала не будет уже столь близко к значению равновесного натриевого потенциала, поэтому потенциал действия будет меньшим по амплитуде. РАСПРОСТРАНЕНИЕ ВОЗБУЖДЕНИЯ Нервные клетки способны передавать возникшее в них возбуждение другим клеткам: нервным или же клеткам других органов — мышечным, секреторным, расположенным от сомы возбужденной нервной клетки иногда на довольно значительных расстояниях (до 1 м). Несмотря на большое разнообразие нервных клеток в организме, сообщаются они между собой с помощью двух основных типов электрических сигналов: 1) медленно изменяющихся, градуальных, т. е. не имеющих фиксированную амплитуду, и 2) импульсных потенциалов с определенной амплитудой, возникающих по закону «все или ничего» — потенциалов действия. Возбуждение из нервных клеток распространяется по их отросткам—нервным волокнам (аксонам или дендритам). По своему строению нервные волокна с точки зрения электропроводящих путей подобны в какой-то мере проложенному под морской водой электрическому кабелю. При этом цитоплазма волокна, представляющая солевой раствор и хорошо проводящая электрический ток, служит аналогом металлического проводника. Не-миелинизированные нервные волокна покрыты мембраной, которая проводит электрический ток значительно хуже — аналог изолирующей оболочки кабеля. Идеальным изолятором является миелиновая, оболочка мякотных волокон, но она местами прерывается проводящей клеточной мембраной через 0,9...2 мм. Роль морской воды, которая, как известно, по своему составу представляет солевой раствор, играет внеклеточная жидкость. При поступлении электрического сигнала в наш биологический кабель электрический ток будет распространяться по нему в соответствии с его электрическими свойствами, а точнее — в соответствии с его электрическим сопротивлением ионному току цитоплазмы и мембраны. Эти свойства можно проиллюстрировать с помощью эквивалентной электрической схемы (рис. 2.16), в которой участки цитоплазмы и мембраны соответственно обозначены сопротивлениями // и /-„.Сопротивления изображены как дискретные элементы лишь для удобства, на самом деле такого разделения в немиели-низированных нервных волокнах нет. Для миелинизированного нервного волокна гт обозначает только сопротивление мембраны в области перехвата Ранвье. Сопротивление волокна на участке, покрытом миелином, имеет очень большую величину по сравнению с сопротивлением мембраны перехвата Ранвье, и поэтому им можно пренебречь. В этом случае дискретность элементов на схе- I I I Мембрана |
* i
t -VW—» гт -VA—♦ к Источник тока Рис. 2.16. Свойства (кабельные) нервного волокна: А — эквивалентная электрическая схема: г,— электрическое сопротивление участка цитоплазмы; гт — электрическое сопротивление участка мембраны; //—ионный ток в цитоплазме; /. — ионный ток через мембрану; стрелками показано направление ионного тока; Vq, V\, V2, V} — потенциалы в точках цитоплазмы волокна, удаленных на различные расстояния от источника тока; Б— экспоненциальное затухание электрического сигнала Va с увеличением расстояния л вдоль нервного волокна ме приобретает электрофизиологический смысл. На схеме стрелками показано ветвление электрического тока от источника. Согласно первому закону Кирхгофа сумма всех токов, выходящих из источника тока, должна быть равна сумме всех токов, входящих в него. Из этого закона, а также закона Ома следует, что в точках ветвления ток будет распределяться таким образом, что его величина через отходящий от этой точки участок будет пропорциональна электрическому сопротивлению данного участка. При включении ток соответственно распределится по всем параллельно и продольно расположенным сопротивлениям. Так, при каждом увеличении продольного сопротивления г-, продольный ток будет уменьшаться, поскольку при последовательном соединении сопротивления складываются. В каждой точке ветвления ток будет распределяться. Часть его будет уходить через сопротивление мембраны гт, а часть — через г,-. В результате этого трансмембранный ток, текущий через гт, будет уменьшаться по мере удаления от источника тока и в конце концов будет равен нулю. Математический анализ характера снижения трансмембранных потенциалов в различных участках нервного волокна показал, что он зависит от соотношения между электрическими сопротивлениями этих участков и имеет вид экспоненты (см. рис. 2.16). Из схемы следует, что распространение ионного тока вдоль цитоплазмы происходит с меньшей степенью затухания, чем меньше ее продольное электрическое сопротивление. В то же время уменьшение сопротивления мембраны усиливает утечку тока во внешнюю среду и способствует более быстрому затуханию тока вдоль волокна. Электрический ток распространяется с меньшими потерями вдоль миелинизированного нервного волокна, поскольку изолирующие свойства миелиновой оболочки снижают утечку тока через поверхность волокна. Вместе с тем вычисления и измерения электрического сопротивления мембраны и цитоплазмы показали, что даже в самых толстых нервных волокнах позвоночных животных их значения составляют миллионы ом. Проходя через такое сопротивление, электрический ток значительно снижает свою величину, поэтому электрический импульс может пассивно распространяться в этих волокнах на расстояние в несколько миллиметров. Таким образом, данный способ распространения электрического потенциала (электрического возбуждения) неприемлем для нервных клеток, имеющих волокна протяженностью несколько десятков или сотен миллиметров. В этих случаях в клетках для распространения возбуждения участвует регенеративный механизм генерации электрического возбуждения. В предыдущем разделе мы выяснили, что в покое нервная клетка имеет мембранный потенциал отрицательной полярности на внутренней стороне мембраны, причем он имеет одинаковую величину и полярность и в соме, и в нервных отростках. Допустим, в результате воздействия какого-либо внешнего или внутреннего
S - 3389 источника раздражения определенный участок нервного волокна возбуждается. В соответствии с этим лавинообразно увеличивается проводимость для ионов натрия и внутренняя поверхность мембраны становится на время положительной. В соответствии с законами электричества электрический (ионный) ток будет распространяться от положительного полюса к отрицательному. Петли тока будут проходить вдоль нервного волокна по цитоплазме и через мембрану невозбужденных участков. В результате мембранный потенциал будет сдвигаться к пороговому значению, и в случае его превышения проницаемость ионов натрия начнет регенеративно увеличиваться с последующим возникновением потенциала действия. Появление потенциала действия в новом участке вызывает местные токи, деполяризующие и возбуждающие следующие участки нервного волокна (рис. 2.17, А). Мы описали процесс распространения потенциала действия в немиелинизированном нервном волокне. В миелинизированном волокне он будет несколько иной. В частности, из-за того что участки мембраны между перехватами Ранвье покрыты миелином, весь возбуждающий местный ток будет воздействовать только на мембрану в области перехвата Ранвье и возникновение очередного потенциала действия будет происходить только в последующем перехвате (рис. 2.17, Б). Если распространение в безмя-котном нервном волокне происходит плавно и напоминает движение горящего участка в бикфордовом шнуре взрывного устройства, то в мякотном волокне возбуждение будет распространяться скачкообразно, или, как часто используют термин, сальтаторно, от перехвата к перехвату. Таким образом, распространяющийся по нервному волокну сигнал постоянно усиливается и поддерживается на одинаковом уровне. Порог деполяризации для возбуждения мембраны составляет около 20 мВ, тогда как обычная деполяризация мембраны при максимальной амплитуде потенциала действия равна 100... 120 мВ. Следовательно, при генерации потенциала действия происходит усиление электротонического сигнала в 5...6 раз. Нужно отметить, что ток, входящий в нервное волокно в месте возбуждения, частично распространяется и назад, т. е. в направлении, противоположном нервному импульсу. Однако этот
Рис. 2.17. Распространение нервного импульса в немиелинизированном (А) и миелинизированном (Б) нервном волокне: а — возбужденный (деполяризованный) участок мембраны нервного волокна; 6— участок мембраны нервного волокна, находящийся в состоянии покоя. Прерывистыми стрелками показано распространение ионного тока. Вверху стрелка указывает направление распространения нервного импульса
ток не вызовет возбуждение мембраны, поскольку ее участки, лежащие сзади от распространяющейся волны возбуждения, находятся в состоянии абсолютной рефрактерности. Калиевая проницаемость в них увеличена, а натриевые каналы временно инакти-вированы. Все это служит надежным блоком для возникновения потенциала действия и распространения вдоль нервного или мышечного волокна. С какой же скоростью распространяются потенциалы действия в нервной системе? В 30-е годы XIX в. один из крупнейших физиологов И. Мюллер заявил, что скорость распространения возбуждения измерить невозможно, поскольку волна возбуждения (или, говоря современным языком, потенциал действия) — электрический импульс и он должен проводиться со скоростью света, т. е. 3 • 1010 см/с. Учитывая малые размеры нервов и мышц и несовершенство регистрирующих приборов того времени, измерить такую скорость, конечно, было невозможно. Однако 15 лет спустя ученик Мюллера, впоследствии знаменитый физиолог, Г. Гельм-юльц с помощью несложной установки (рис. 2.18) показал, что скорость распространения возбуждения в нервах и мышцах в 10 млн раз меньше скорости света. В своих опытах Гельмгольц использовал нервно-мышечный препарат. Он раздражал нерв в двух точках, отстоящих друг от друга на расстоянии 3 см, и измерял время с момента подачи стимула до наступления максимума сокращения. Предположим, что при раздражении участка нерпа, расположенного ближе к мышце на 3 см, время наступления максимума сокращения уменьшилось на 0,001 с. Тогда получается, что волна возбуждения прошла 3 см нерва за 0,001 с. Следова-
тельно, возбуждение по нервному волокну распространяется со скоростью V= S/l = 3 см/0,001 с = 3 • 103 см/с = 30 м/с. На основании своих наблюдений Гельмгольц сделал вывод, что проведение волны возбуждения (нервного импульса) — это более сложный процесс, чем простое продольное проведение тока в нервном волокне. Как уже указывалось, введение Эрлангером и Гассером в 30-х годах XX в. в практику электрофизиологического эксперимента безынерционного катодного осциллографа с электронным усилителем позволило весьма точно измерить проведение потенциалов действия в различных нервных волокнах. Оказалось, что скорость проведения возбуждения зависит от диаметра волокна, а также наличия у нервного волокна миелиновой оболочки. У высших позвоночных животных наименьшая скорость проведения, составляющая 0,5...2 м/с, была зарегистрирована в тонких немиелинизированных волокнах диаметром 0,5... 1 мкм. Наибольшей скоростью (70... 120 м/с) обладают самые толстые миелинизи-рованные волокна диаметром 15...25 мкм. Скорость распространения нервного импульса в значительной мере зависит от того, как быстро участок мембраны деполяризуется местными токами до порогового уровня. А это согласно схеме (см. рис. 2.16) будет происходить тем быстрее, чем меньше продольное сопротивление цитоплазмы. Известно, что электрическое сопротивление проводника связано с его длиной и диаметром следующим соотношением: R = pl/S, где Л—сопротивление, Ом; р —удельное сопротивление материала; /—длина проводника, м; S— площадь поперечного сечения проводника. В свою очередь, S = яг2, где г — радиус проводника. Следовательно, R = р//лг2, т. е. чем больше радиус проводника, тем меньше его сопротивление, и поэтому более толстые нервные волокна имеют большую скорость проведения. Второй важный фактор, способствующий более быстрой деполяризации мембраны, — это снижение утечки тока через мембрану волокна. В связи с этим ми-елинизированные нервные волокна при равных диаметрах с немиелинизированными имеют большую скорость проведения. Кроме того, было обнаружено, что плотность натриевых каналов в мембране перехвата Ранвье в несколько раз выше, чем в мембране немиелинизированных волокон. Это дополнительно способствует более быстрой деполяризации мембраны в области перехвата Ранвье и соответственно увеличивает скорость проведения по волокну.
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 580; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.015 с.) |


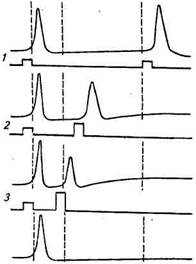
 мости — рефрактернос-т и. Наличие фазы рефрактерности, сопровождающее окончание возбуждения, было впервые установлено в конце XIX в. Мареем на сердце лягушки. Он обнаружил, что после сокращения сердца очередное сокращение нельзя вызвать в течение периода, равного десятым долям секунды, независимо от амплитуды и длительности раздражающего стимула. В нервных клетках период невозбудимости оказался значительно короче, чем в мышечных. При уменьшении интервала раздражения между двумя раздражающими электрическими стимулами величина потенциала действия в ответ на второй стимул становится все ниже и ниже. А если повторный стимул наносится во время генерации потенциала действия или сразу же после его окончания, то второй потенциал действия не генерируется (рис. 2.15). Период, в течение которого потенциал действия на второй раздражающий стимул не возникает, получил название абсолютного рефрактерного периода. Он составляет для нервных клеток позвоночных животных 1,5...2 мс. После периода абсолютной рефрактерности наступает относительный рефрактерный период, который характеризуется: 1) повышенным порогом раздражения по сравнению с исходным состоянием (т. е. для того чтобы возник повторный потенциал действия, необходим ток большей величины); 2) снижением амплитуды потенциала действия. По мере окончания периода относительной рефрактерности возбудимость повышается до исходного уровня и величина порогового раздражения уменьшается также до первоначального значения.
мости — рефрактернос-т и. Наличие фазы рефрактерности, сопровождающее окончание возбуждения, было впервые установлено в конце XIX в. Мареем на сердце лягушки. Он обнаружил, что после сокращения сердца очередное сокращение нельзя вызвать в течение периода, равного десятым долям секунды, независимо от амплитуды и длительности раздражающего стимула. В нервных клетках период невозбудимости оказался значительно короче, чем в мышечных. При уменьшении интервала раздражения между двумя раздражающими электрическими стимулами величина потенциала действия в ответ на второй стимул становится все ниже и ниже. А если повторный стимул наносится во время генерации потенциала действия или сразу же после его окончания, то второй потенциал действия не генерируется (рис. 2.15). Период, в течение которого потенциал действия на второй раздражающий стимул не возникает, получил название абсолютного рефрактерного периода. Он составляет для нервных клеток позвоночных животных 1,5...2 мс. После периода абсолютной рефрактерности наступает относительный рефрактерный период, который характеризуется: 1) повышенным порогом раздражения по сравнению с исходным состоянием (т. е. для того чтобы возник повторный потенциал действия, необходим ток большей величины); 2) снижением амплитуды потенциала действия. По мере окончания периода относительной рефрактерности возбудимость повышается до исходного уровня и величина порогового раздражения уменьшается также до первоначального значения.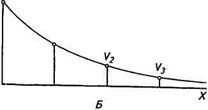 Внеклеточная среда V0
Внеклеточная среда V0



