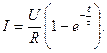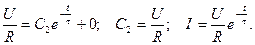Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динамика автоматических системСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Исследование движения (переходных процессов) автоматических систем под действием задающих и возмущающих воздействий может быть выполнено по уравнениям динамических режимов. Переходные процессы в большинстве элементов системы характеризуются инерционностью (наличие массы, индуктивности, емкости) и аналитически могут быть описаны дифференциальными уравнениями, которые определяют изменение управляемой величины во времени при заданном характере входных и возмущающих воздействий. Дифференциальные уравнения отдельных элементов и всей системы составляются по законам физики. Совокупность всех уравнений, отражающих характер протекания переходного процесса, носит название уравнений процессов управления.
1.8. Фомы записи уравнений элементов автоматической системы.
Запишем дифференциальное уравнение движения системы в классическом виде: a0dnxвых/dtn + a1dn-1xвых/dtn-1 +…+ an-1dxвых/dt + anxвых = F(xвх, x!вх, x!!вх,…) ± f(t). Здесь F(xвх, x!вх, x!!вх,…) – функция входного воздействия; f(t) – возмущающее воздействие. Общий интеграл (решение) этого уравнения определяется суммой Хвых = хвын + хсв, где хвых – общий интеграл, определяющий изменение выходной величины во времени; хвын – частное решение уравнения, определяющее вынужденное установившееся движение; хсв – решение однородного дифференциального уравнения, определяющее свободное движение. Составляющие интеграла от свободного и вынужденного движения определяются отдельно. Для однородного дифференциального уравнения в общем виде, полагая правую часть равной нулю, получим: а0dnxсв/dtn + a1dn-1xсв/dtn-1 +… +an-1dxсв/dt + anxсв = 0. Интеграл однородного дифференциального линейного уравнения с постоянными коэффициентами (для случая различных вещественных корней), определяется суммой: xсв = С1еa1t + C2ea2t +…Cneant, Ci – произвольные постоянные числа, aI – корни характеристического уравнения, которое имеет вид: a0an + a1an-1 +…+ an-1a + an = 0. На практике встречаются случаи наличия кратных вещественных и комплексных корней; тогда интеграл для свободного движения будет иметь гармонические составляющие. После определения корней с учетом начальных условий вычисляют постоянные числа, входящие в интеграл свободного движения. После решения дифференциального уравнения оценивают ошибку регулирования системы в динамике. Dхвых = хн – хвых = хн – хвын – хсв, где Dхвых – ошибка регулирования; хн – заданное значение управляемой величины; хвых – действительное значение управляемой величины. Для алгебраизации дифференциального уравнения применяется операционная форма записи. Если к переменной x(t) применить преобразование Лапласа, то получим так называемое изображение функции x(t): x(p) = ò x(t) e-pt dt, где p = s +jw новая функция комплексного переменного. При этом первая производная от х будет иметь изображение px(p), вторая—p2x(p), третья --p3x(p) и т.д. Интеграл от х будет иметь изображение х(р)/p. Если применить преобразование Лапласа к ранее записанному дифференциальному уравнению, то при нулевых начальных условиях оно примет вид (a0рn + a1pn-1 +…+ an-1p + an)xсв(р) = 0. Решив операционное уравнение, мы найдем не оригинал x(t), а только его изображение x(p). Определить оригинал по изображению можно или с помощью таблицы оригиналов и их изображений, или непосредственно, применив обратное преобразование Лапласа. В качестве примера произведем расчет переходных процессов при включении электрической цепи постоянного тока, содержащую индуктивность и активное сопротивление:
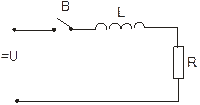
Рис. 1.8. Включение электрической цепи, содержащей индуктивность.
Дифференциальное уравнение цепи
соответствующее однородное уравнение:
Корень этого уравнения α = -R/L. Величину обратную α обозначим τ. Эта величина называется постоянной времени цепи, содержащей индуктивность. Свободная составляющая тока в цепи определится
Установившееся (вынужденное) значение тока Полное значение тока в переходной период
Для этого учтем начальные условия. В момент включения (t = 0) ток равен нулю I = 0, 0 = C1 + U/R; C1 = - (U/R); При отключении (при t = 0, I0 = U/R Iy = 0)
|
||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 619; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

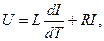
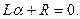

 .
.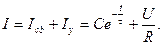 Определим постоянную интегрирования С.
Определим постоянную интегрирования С.