Типовые звенья автоматических систем. Частотные характеристики. Устойчивость. Переходные процессы.

 

Любую сколь угодно сложную САР можно разбить на ряд простейших элементов — звеньев.

Звено — это элемент (часть) автоматической системы, который имеет определенные статические и динамические свойства.

 

Рис. 1.9. Графическое изображение звена.

 

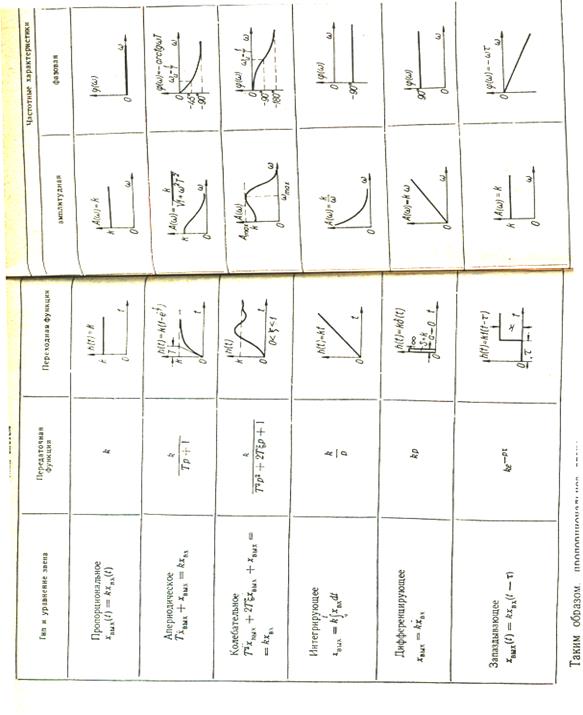
Звенья САР характеризуются следующими признаками.

1. Передаточная функция — отношение выходной величины сигнала к входной величине.

W = X_вых / X_вх.

 

2. Частотные характеристики — зависимость выходной величины от

частоты входного сигнала. Строятся они по следующим правилам: на вход звена подается сигнал различной частоты, при этом на выходе фиксируется амплитуда и фаза выходного сигнала (пример с грузом на пружине).

По этим данным строятся также отдельно амплитудные и фазовые характеристики, а также логарифмические ЛАЧХ и фазовые ФАЧХ характеристики.

3. Переходная функция —характер зависимости выходной величины от

времени при воздействии на вход звена ступенчатой единичной функции.

 

Характеристики типовых звеньев автоматических систем.

 

Несмотря на большое многообразие автоматических систем, практически все они построены из ограниченного числа типовых звеньев (Табл. 1.1).

1.Пропорциональное (усилительное) звено. Примеры: делитель

напряжения, потенциометрический датчик, усилительный каскад, механический редуктор и др. Для этого звена характерна пропорциональная зависимость между входной и выходной величинами.

Передаточная функция звена:

 

W = X_вых/X_вх =К,

где К—коэффициент передачи.

Таким образом, пропорциональное звено мгновенно копирует входной сигнал, изменяя его масштаб в К раз. Переходной процесс отсутствует. Выходной и входной сигнал находятся в фазе.

F(w) = 0.

Амплитудная характеристика А(w) = К. Амплитудно-частотные характеристики АЧХ пропорционального звена не зависят от частоты.

1. Апериодическое звено. Описывается дифференциальным уравнением:

T(dx_вых/dt) + x_вых = кх_вх.

Передаточная функция. Применив преобразование Лапласа, получим:

W(p) = K/(Tp + 1).

Пример: включение емкости через резистор, u = ri + u_c; I = dq/dt = d(Cu_c)/dt = C(du_c/dt)

то rC(du_c/dt) + u_c = u; или Tpu_c + u_c = u; u_c/u = W(p) = 1/(Tp + 1); T = rC.

(пример про индуктивность)

Переходная функция достигает своего установившегося значения К не сразу, а постепенно по экспоненциальному закону. Тем самым апериодическое звено отражает инерционность процесса. Мерой инерционности является постоянная времени Т: переходной процесс заканчивается при t = 3T.

Амплитудно-фазовую характеристику найдем из передаточной функции заменой Р на jw

W = K/(1 + jw).

Выделим из этого выражения действительную и мнимую части и тем самым найдем:

вещественную

P(w) = K/(1 + w²T²)

и мнимую

Q(w) = - KwT/(1 + w²T²)

частотные характеристики.

Теперь определим амплитудную

A(w) = Ö(P² + Q²) = K/Ö(1 + w²T²)

и фазовую j = arctg {Q(w)/P(w)} = - arctg(wT)

частотные характеристики, которыми наглядно отображаются частотные свойства звена.

Из анализа амплитудной частотной характеристики А(w) следует, что апериодическое звено обладает свойством фильтра: хорошо пропускает сигналы малых частот и плохо – больших.

Из анализа фазовой частотной характеристики j(w) следует, что выходные колебания отстают от входных. Это отставание изменяется в пределах от 0^о до --90⁰. На частоте w_с = 1/T j (w) = -45⁰.

3.Колебательное звено. Рассмотрим электрическую цепь, состоящую

из последовательно включенных резистора R, индуктивности L, емкости С. Динамические процессы в такой цепи будут описываться дифференциальным уравнением второго порядка

L (d²q/dt²) + R (dq/dt) + (1/C) q = u, где q—заряд емкости С.

Передаточная функция такого звена

W(p) = K /(T²p² + 2Txp + 1), где

x = R / (Ö (L/C))—коэффициент затухания цепи.

Переходный процесс зависит от коэффициента затухания x.

При 0<x<1 переходной процесс колебательный, причем, чем меньше, x тем колебания более интенсивны. В идеальном случае x = 0. Это значит, что потери энергии отсутствуют и переходной процесс будет незатухающим.

Если x >> 1, то потери энергии настолько велики, что переходной

процесс перестает быть колебательным. В этом случае звено называют апериодическим второго порядка, и его можно заменить двумя последовательно соединенными апериодическими звеньями.

АЧХ колебательного звена А(w) имеет максимум А_max на резонансной частоте w_мах. Чем меньше x, тем больше А_мах.

ФЧХ. Колебательное звено создает отрицательный сдвиг фаз, который изменяется от 0⁰ при w = 0 до –180⁰ при w = ¥. На частоте w_с = 1/Т j (w) = --90⁰.

4.Интегрирующее звено. Называется такое звено, выходная величина

которого пропорциональна интегралу по времени от входной величины:

х_вых(t) = K ò х_вх (t)dt.

Передаточная функция W(p) = K/p.

Переходная функция. При постоянном (ступенчатом) входном сигнале выходной сигнал интегрирующего звена изменяется с постоянной скоростью, поэтому его переходная функция непрерывно возрастает по линейному закону.

Отличительным свойством интегрирующего звена является то, что после прекращения действия входного сигнала выходной сигнал звена остается на том уровне, на котором он был в момент исчезновения входного сигнала (т. Е. Обладает свойством запоминания последнего значения выходной величины).

Примером интегрирующего звена безинерционный электродвигатель обладает бесконечной «памятью». Действительно, если прекратить подачу входного напряжения, то вал двигателя остановится, и будет сохранять то угловое положение, которое было достигнуто к моменту исчезновения напряжения.

АЧХ с ростом частоты w убывает.

ФЧХ Звено вносит отрицательный сдвиг фаз, который не зависит от частоты и равен -90⁰.

5.Дифференцирующее звено. Его выходная величина

пропорциональна производной по времени от выходной:

х_вых(t) = K (dx_вх(t)/ dt).

Примером является тахогенератор, так как его напряжение пропорционально скорости вращения якоря, которая является производной по времени от угла поворота.

Передаточная функция W (p) = K p.

Переходная функция. Звено не пропускает постоянного по величине сигнала. Однако при подаче на его вход ступенчатого сигнала на выходе будет импульс.

АЧХ A(w) = K p. Имеет возрастающий характер, т.е. с увеличением частоты увеличивается и амплитуда выходного сигнала.

ФЧХ Звено вносит опережение по фазе, равное +90⁰ и не зависящее от частоты.

6.Запаздывающее звено. Звено, которое передает сигнал без искажений, но при этом выходной сигнал по отношению ко входному запаздывает на постоянную величину t, называется запаздывающим. Таким свойством обладает, например, релейный усилитель, причем запаздывание определяется временем срабатывания реле.

Передаточная функция W(p) = Ke^-pt.

Переходная функция --подобна переходной функции усилительного, но смещена по времени на t.

АЧХ --также подобна усилительному.

ФЧХ звено создает отрицательный сдвиг фаз, который линейно зависит от частоты.

Табл. 1.1.

Характеристики типовых звеньев автоматических систем.