
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исследование функции на экстремум с помощью второй производной. Точки перегиба.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Справочный материал Второй достаточный признак существования экстремума. Если в критической точке вторая производная функции отрицательна, то функция в этой точке имеет максимум. Если вторая производная положительна, — минимум. Говорят, что функция у = f(х) имеет выпуклость вверх (выпуклость), если график этой функции на (а, b) расположен ниже любой касательной к графику функции на (а, b). Функция выпукла вниз (вогнута) на (а, b), если график этой функции расположен выше касательной на (а,b).
Если функция у = f(x) имеет на интервале (а, b ) вторую производную и f "(х)>0 (f "<0) во всех точках (а, b), то функция у = f (х) имеет на (а, b) вогнутость (выпуклость). Точка перегиба функции — это точка, в которой направление выпуклости меняется на обратное. Например, функция у = х3 имеет точку перегиба х = 0:
Необходимое условие точки перегиба. Если функция у = f (х) имеет перегиб в точке х, и существует вторая производная в этой точке, тогда f "(х0) = 0. Достаточное условие точки перегиба. Пусть функция у = f(х) имеет вторую производную в некоторой окрестности точки х0. Тогда, если в пределах этой окрестности f "(х) имеет разные знаки слева и справа от точки х0, функция f(х) имеет перегиб в точке х0.
Асимптоты кривой. Справочный материал. Определение: Асимптотой кривой Функция Значит, если то прямая Пример 4.5.
РЕШЕНИЕ:
где (-0) и (+0)- символические записи соответственно отрицательной и положительной бесконечно малой величины. График вблизи асимптот представлен на рис. 4.8.
Рис.4.8 Пример 4.6. Найти вертикальные асимптоты функции
РЕШЕНИЕ: Для уточнения поведения
График вблизи асимптот изображён на рис. 4.9. Функция
Рис.4.9 Пусть функция
По определению асимптоты Аналогично находится уравнение наклонной асимптоты при Пример 4.7. Найти асимптоты кривой РЕШЕНИЕ:
Вертикальная асимптота
Наклонная асимптота
Наклонная асимптота:
|
|||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 1024; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |



 называется такая прямая, расстояние до которой от переменной точки, движущейся по бесконечной ветви кривой, стремится к нулю.
называется такая прямая, расстояние до которой от переменной точки, движущейся по бесконечной ветви кривой, стремится к нулю. имеет вертикальные асимптоты в точках, где функция терпит бесконечный разрыв, т.е. если
имеет вертикальные асимптоты в точках, где функция терпит бесконечный разрыв, т.е. если 
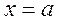 есть точка разрыва 2-го рода,
есть точка разрыва 2-го рода, - вертикальная асимптота кривой.
- вертикальная асимптота кривой. Найти её вертикальные асимптоты.
Найти её вертикальные асимптоты. терпит бесконечный разрыв при
терпит бесконечный разрыв при 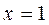 , так как
, так как  Прямая
Прямая  и
и  :
: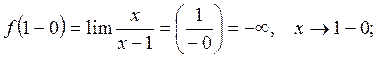



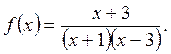
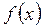 имеет две вертикальные асимптоты:
имеет две вертикальные асимптоты:  и
и 
 и
и 




 не имеет вертикальных асимптот. (Почему?) Функция
не имеет вертикальных асимптот. (Почему?) Функция 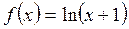 имеет вертикальную асимптоту
имеет вертикальную асимптоту  Кроме вертикальных асимптот, функция может иметь и наклонные асимптоты, в частном случае - горизонтальные. Эти асимптоты находят по уравнению прямой с угловым коэффициентом
Кроме вертикальных асимптот, функция может иметь и наклонные асимптоты, в частном случае - горизонтальные. Эти асимптоты находят по уравнению прямой с угловым коэффициентом  при
при 

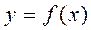 имеет наклонную асимптоту
имеет наклонную асимптоту  при
при  Найдём
Найдём 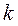 и
и  Обозначим через
Обозначим через (1)
(1) Разделим равенство (1) на х и перейдём к пределу при
Разделим равенство (1) на х и перейдём к пределу при  где
где 
 причём наклонная асимптота при
причём наклонная асимптота при  существует тогда и только тогда, когда оба эти предела существуют и конечны, в противном случае кривая
существует тогда и только тогда, когда оба эти предела существуют и конечны, в противном случае кривая  не имеет наклонной асимптоты.
не имеет наклонной асимптоты. Если
Если  то асимптота будет горизонтальной и её уравнение имеет вид
то асимптота будет горизонтальной и её уравнение имеет вид 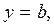 где
где 
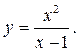

 точка бесконечного разрыва функции (2-го рода).
точка бесконечного разрыва функции (2-го рода). :
: ;
;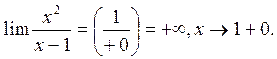
 :
: ;
;
 (рис. 4.10).
(рис. 4.10).



