
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общая схема исследования функций и построение их графиков.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Справочный материал. Способ построения графика функции “по точкам” не является совершенным. Использование аппарата производной при построении графика функции значительно облегчает эту задачу. При исследовании и построении графиков функций можно использовать следующую схему. Обратите особое внимание на эту схему, так как по ней будем проводить изучение свойств и построение графиков основных элементарных функций.
1. Найти область определения функции. 2. Выяснить, не является ли функция чётной, нечётной, периодической. 3. Найти точки пересечения графика с осями координат и интервалы знакопостоянства функции (если это не вызывает затруднений). 4. Исследовать функцию на непрерывность, найти и исследовать точки разрыва. 5. Найти асимптоты графика функции. 6. Найти промежутки монотонности функции и её экстремумы. 7. Найти промежутки выпуклости, вогнутости. Исследовать функцию на перегиб. 8. Построить график функции, используя полученные результаты исследования. Для уточнения графика можно найти несколько дополнительных точек, составив таблицу значений. Примечание. Рекомендуется результаты исследования наносить на чертёж постепенно, по ходу работы по схеме. В этом случае ошибка, которую можно допустить при исследовании, обнаруживается сразу, как только данный пункт схемы придёт в противоречие с предыдущими результатами.
Пример 4.8. Построить график функции РЕШЕНИЕ: 1. Область определения функции
2. Функция не является ни чётной, ни нечётной (общего вида), так как 3. Точки пересечения с осью
Кривая с осью
Таблица 6.
Знаки функции легко определить, если взять по одной пробной точке в каждом интервале. Например, 4. Функция элементарная, следовательно, непрерывна в области определения;
где
5. Асимптоты. Из п.4 следует, что Наклонная асимптота
Горизонтальная асимптота
6. Для нахождения промежутков монотонности функции и её экстремумов найдём производную:
Имеем одну критическую точку Составим табл.7, разбив Таблица 7
В точке x =4 локальный максимум 7. Исследуем функцию на перегиб
х =6 - точка, подозреваемая на перегиб.
yII -- +
выпукла 6 вогнута
y
8. Строим график функции (рис. 4.11).
Задания для самостоятельной работы
Исследуйте функцию и постройте её график: А. 1) Б. 1) В. 1) 4)
|
|||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 842; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |



 и
и  Поэтому график функции не симметричен относительно оси
Поэтому график функции не симметричен относительно оси  и начала координат. Функция непериодическая.
и начала координат. Функция непериодическая.

 не
не  Интервалы знакопостоянства укажем в табл.6.
Интервалы знакопостоянства укажем в табл.6. т.е.
т.е.  и т.д.
и т.д. точка разрыва функции. Исследуем её:
точка разрыва функции. Исследуем её:

 точка разрыва 2-го рода.
точка разрыва 2-го рода.





 при
при 

 на интервалы.
на интервалы.

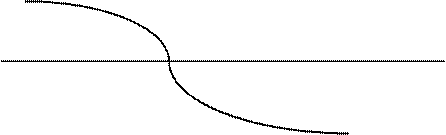

 Рис.4.11
Рис.4.11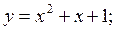 2)
2)  3)
3)  4)
4) 
 2)
2)  3)
3)  4)
4) 
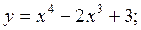 2)
2)  3)
3) 
 5)
5) 



