
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства пределов. Простейшие пределы.Содержание книги
Поиск на нашем сайте Практическое вычисление пределов основывается на следующих свойствах. Если существуют конечные пределы 1. 2. 3. 4. Для
5. Если предел одной или нескольких функций равен бесконечности, то можно воспользоваться следующим соотношениями:
для 6. Если предел функции равен 0, то Для того, чтобы найти предел элементарной функции, когда аргумент стремится к значению, принадлежащему области определения этой функции, нужно в выражение функции вместо аргумента подставить его предельное значение. Примеры. 1.
2.
3.
Или
Раскрытие неопределенностей различных типов. Случаи, в которых подстановка предельного значения в функцию не дает значения предела называют неопределенностями; к ним относят неопределенности видов:
Устранить неопределенность удается часто с помощью алгебраических преобразований.
Пример. Найти РЕШЕНИЕ
Ответ данной задачи будем использовать далее как заранее известный факт. 2.2.1. Раскрытие неопределенности типа В случае степенных функций необходимо выносить за скобку в числителе и знаменателе дроби x с наибольшим показателем степени среди всех слагаемых дроби; в случае показательных функций за скобку выносится наиболее быстро возрастающее слагаемое, среди всех слагаемых дроби. После сокращения дроби неопределенность устраняется. Пример.
Задания для самостоятельной работы
2.2.2. Раскрытие неопределенности типа В этом случае обычно используются следующие приемы: a) алгебраические преобразования числителя и знаменателя дроби, приводящие к формулам сокращенного умножения; неопределенность устраняется после сокращения дроби; b) вынесение в числителе и знаменателе дроби степени х с наименьшим показателем; c) Деление числителя дроби на ее знаменатель; d) Эквивалентность бесконечно малых величин; e) Первый замечательный предел. Примеры. a)
(дополнили числитель до разности квадратов b) c)
d) Примеры эквивалентных бесконечно малых величин при
Предел отношения двух бесконечно малых величин не изменится, если эти бесконечно малые величины заменить им эквивалентными. Пример.
e)
Примеры. 1)
2)
2.2.3. Раскрытие неопределенности типа В этом случае выражение, стояще под знаком предела представляет собой степенно-показательную функцию, в основании которой необходимо выделить целую часть дроби (которая должна быть равна 1). Неопределенность устраняется при помощи «второго замечательного предела». 1)
Примеры 1) 2)
3)
2.2.4. Раскрытие неопределенности типа Если функция, стоящая под знаком предела представляет собой алгебраическую сумму дробей, то неопределенность устраняется или приводится к неопределенности Примеры. 1)
2)
Задания для самостоятельной работы
|
||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 835; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 ,
,  , то:
, то:

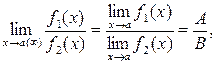
 т.е.
т.е. 
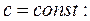



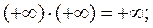











 т.к.
т.к.  при
при  является б.б.в., то
является б.б.в., то  при
при  по определению бесконечно малой величины. Или
по определению бесконечно малой величины. Или  ;
; т.к.
т.к.  при
при  является бесконечно малой величиной, тогда
является бесконечно малой величиной, тогда 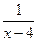 -бесконечно большая величина;
-бесконечно большая величина; 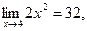 т.е. функция
т.е. функция  является бесконечно большой величиной, т.е.
является бесконечно большой величиной, т.е.  по определению бесконечно большой величины.
по определению бесконечно большой величины.

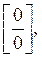






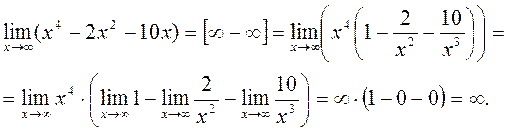
 .
.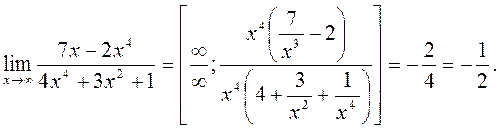
 3)
3) 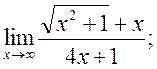
 4)
4) 
 .
.


 , а знаменатель до разности кубов
, а знаменатель до разности кубов  ).
).


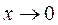 :
:


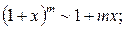




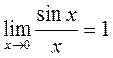 - первый замечательный предел.
- первый замечательный предел.

 .
. ; 2)
; 2) 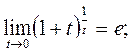





 после приведения дробей к общему знаменателю. Если функция представляет собой сумму иррациональных выражений, то неопределенность или устраняется, или приводится к виду
после приведения дробей к общему знаменателю. Если функция представляет собой сумму иррациональных выражений, то неопределенность или устраняется, или приводится к виду  путем домножения и деления функции на одно и то же (сопряженное выражение), приводящее к формулам сокращенного умножения.
путем домножения и деления функции на одно и то же (сопряженное выражение), приводящее к формулам сокращенного умножения.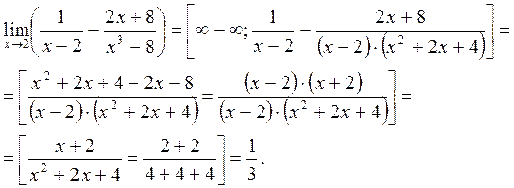


 4)
4) 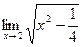 7)
7)  10)
10)  13)
13)  16)
16)  19)
19)  22)
22) 
 5)
5)  8)
8)  11)
11)  14)
14)  17)
17) 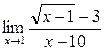 20)
20)  23)
23) 
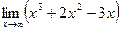 6)
6)  9)
9)  12)
12) 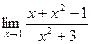 15)
15)  18)
18)  21)
21)  24)
24) 
 28)
28) 
 29)
29) 
 30)
30) 



