Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приближенное решение уравненийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Действительные корни уравнения Пользуясь этим, можно находить приближенные значения действительных корней уравнений, путем построения соответствующих кривых. Но этим графическим методом можно получить лишь грубо приближенные значения корней уравнения. Поэтому графический метод обычно применяется лишь как вспомогательное средство для определения числа действительных корней уравнения и для их отделения. Затем, после отделения корней, они могут быть вычислены с любой желаемой точностью, посредствам аналитических методов.
пример выполнения расчетно-графической работы Задание. Решить графически уравнение И уточнить его корни методом половинного деления, методом хорд и касательных
1. Графический метод.
Выделяем графический интервал:
2. Уточнение корней методом половинного деления. Выполним методом половинного деления, 3 итерации (метод бисекции). За начальное приближение то Если
1) Первое приближенное значение корня:
Выбираем промежуток
2) Второе приближенное значение корня
Выбираем промежуток
3) Третье приближенное значение корня
Выбираем промежуток Если требуется вычислить корень с точностью
3.Уточнение корней уравнения методом хорд: Хорда проведена слева.    Рис. 4.13 Рис. 4.13
Хорда проведена справа.
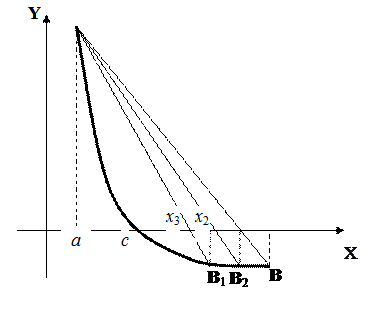
Рис. 4.14 Уравнение хорды
Для точки пересечения ее с осью
Сравнивая знаки
При этом гарантируема
4. Уточнение корней уравнения методом касательных (метод Ньютона): Будем считать, что Проведем касательную к кривой
Касательную нужно проводить в том конце отрезка Уравнение касательной: Касательная справа:
Касательная слева:
5. Уточнение корней уравнения методом хорд и касательных:
Рис. 4.17
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 536; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.37.211 (0.008 с.) |

 являются абсциссами точек пересечения кривой
являются абсциссами точек пересечения кривой  с осью
с осью 

 Подбором
Подбором

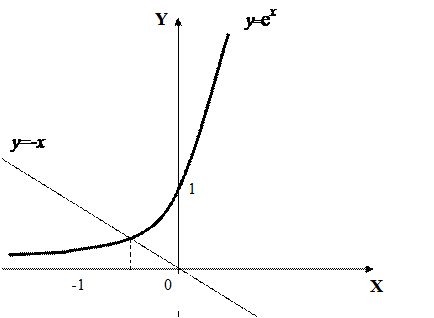 Рис. 4.12
Рис. 4.12
 берут середину отрезка
берут середину отрезка  .
.
 ,
,  , то выбираем ту из половин
, то выбираем ту из половин  , на концах которой
, на концах которой  имеет противоположные знаки. Это значит, что корень лежит в этом промежутке. Затем новый отрезок делим пополам точкой
имеет противоположные знаки. Это значит, что корень лежит в этом промежутке. Затем новый отрезок делим пополам точкой  и выбираем ту половину, на которой лежит корень и т. д.
и выбираем ту половину, на которой лежит корень и т. д.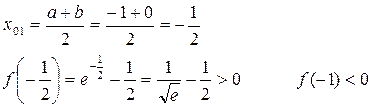


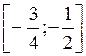
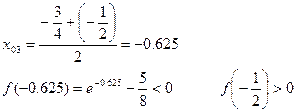

 , то продолжаем процесс до тех пор, пока длина отрезка не станет
, то продолжаем процесс до тех пор, пока длина отрезка не станет 
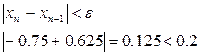


 ;
;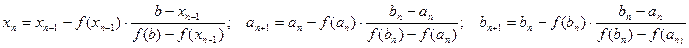
 - хорда проведена слева,
- хорда проведена слева, 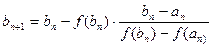 - хорда проведена справа.
- хорда проведена справа.
 - хорда проведена слева
- хорда проведена слева 
 и
и 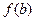 , приходим к выводу, что корень
, приходим к выводу, что корень  . Следующие приближение к корню -
. Следующие приближение к корню -  - точка пересечения хорды
- точка пересечения хорды  с
с  и т. д.
и т. д.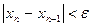

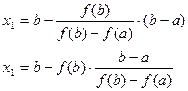 - хорда проведена справа
- хорда проведена справа 
 и
и  знакопостоянны на
знакопостоянны на  .
. (знак функции совпадает со знаком второй производной).
(знак функции совпадает со знаком второй производной).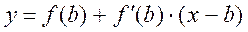
 5
5










 . Хорда проведена слева. Касательная проведена справа.
. Хорда проведена слева. Касательная проведена справа.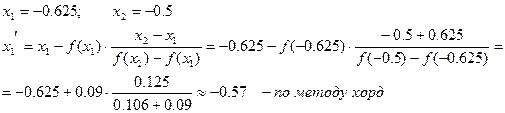

 - по методу касательных.
- по методу касательных.