
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Наибольшее и наименьшее значения функции.Содержание книги
Поиск на нашем сайте
Справочный материал. Часто приходится рассматривать задачи, связанные с нахождением наибольшего или наименьшего значения из всех тех значений, которые функция принимает на некотором отрезке. В отличие от локальных экстремумов, такие значения называются глобальными экстремумами. Если f (x) монотонна на
Пример 4.9. Найти наибольшее и наименьшее значения функции
РЕШЕНИЕ: Отсюда ясно, что наименьшее значение функция принимает на левом конце при x =2, наибольшее - на правом конце при x =5:
Ответ:
Если f (x) непрерывна, но не монотонна на Чтобы найти наибольшее и наименьшее значения функции на
Пример 4.10. Найти наибольшее и наименьшее значения функции
РЕШЕНИЕ: f (x) на
Обе критические точки принадлежат Вычислим значения данной функции в точках
Пример 4.11. Найти наибольшее значение функции
РЕШЕНИЕ: Этот пример отличается от 10(а) тем, что функция рассматривается не на конечном промежутке, а на всей числовой оси, так как Составим табл. 4.5. Таблица 4.5
Из таблицы видно, что функция имеет два максимума:
Кроме того, на Отсюда делаем вывод, что наибольшего значения функция достигает в точке Ответ:
Примеры. 1.Найти наименьшее и наибольшее значения функции РЕШЕНИЯ:Находим критические точки функции. Так как а) В промежутке
б) В промежутке Наименьшего значения в промежутке Задания для самостоятельной работы. 1. Найдите наименьшее и наибольшее значения функции: 1) 2)
2. В. Представьте число 12 в виде суммы двух положительных слагаемых так, чтобы сумма их квадратов была наименьшей.
3.В. Найдите такое число, чтобы его сумма со своим квадратом имела наименьшее значение.
4. Имеется проволока длиной
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 507; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.202.60 (0.006 с.) |

 то наибольшее и наименьшее значение функция принимает на концах отрезка.
то наибольшее и наименьшее значение функция принимает на концах отрезка. на
на 
 для
для  значит, функция
значит, функция  возрастающая на
возрастающая на 





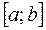 , то наибольшее и наименьшее значения функция может принимать либо в точках экстремума, либо на концах отрезка. Отсюда можно сформулировать следующее правило.
, то наибольшее и наименьшее значения функция может принимать либо в точках экстремума, либо на концах отрезка. Отсюда можно сформулировать следующее правило. , нужно найти все критические точки функции, лежащие внутри
, нужно найти все критические точки функции, лежащие внутри  на отрезке
на отрезке 
 определена и непрерывна. Найдём критические точки, для чего определим производную
определена и непрерывна. Найдём критические точки, для чего определим производную  Она существует во всех точках
Она существует во всех точках 
 и
и 
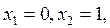
 и
и 
 на R.
на R. Здесь мы не можем найти значения функции на концах промежутка и сравнить их со значениями функции в критических точках. Решить задачу поможет нам нахождение интервалов возрастания и убывания функции:
Здесь мы не можем найти значения функции на концах промежутка и сравнить их со значениями функции в критических точках. Решить задачу поможет нам нахождение интервалов возрастания и убывания функции:  Критические точки:
Критические точки: 

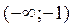 функция возрастает до
функция возрастает до 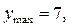 а на
а на  функция убывает от
функция убывает от 
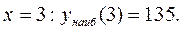


 на промежутке: а)
на промежутке: а)  б)
б) 
 то имеются две критические точки:
то имеются две критические точки:  и
и 
 лежит одна из критических точек:
лежит одна из критических точек: 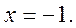 Так как
Так как  то наименьшее значение функции
то наименьшее значение функции  достигается в точке
достигается в точке  и равно 3, а наибольшее – в точке
и равно 3, а наибольшее – в точке  и равно 8. Кратко это можно записать так:
и равно 8. Кратко это можно записать так:


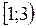 данная функция убывает. Поэтому
данная функция убывает. Поэтому 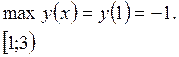
 не принадлежит этому промежутку.
не принадлежит этому промежутку. на отрезке: а)
на отрезке: а)  б)
б) 
 на отрезке: а)
на отрезке: а)  б)
б) 
 метров. Требуется оградить этой проволокой прямоугольный участок земли, одна сторона которого примыкает к стене заводского здания, так, чтобы площадь огороженного участка была наибольшей.
метров. Требуется оградить этой проволокой прямоугольный участок земли, одна сторона которого примыкает к стене заводского здания, так, чтобы площадь огороженного участка была наибольшей.


