Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Коваленко Татьяна ДмитриевнаСодержание книги
Поиск на нашем сайте 51 (07) М – 34
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
МАТЕМАТИКА Часть 1
Учебно-методическое пособие
Самара
УДК 51 (07) ББК 22.1 М 34
Математика. Часть 1. Учебно-методическое пособие. /Составители Е.Э.Лищинская, Т.Д.Коваленко, Н.Я.Лищинский. – Самара: МИР, 2008. – 72 с.
Учебно-методическое пособие «Математика. Часть 1» является составной частью УМКД «Математика» и предназначено для организации самостоятельной работы студентов. Пособие содержит справочные материалы по разделам «Элементы математического анализа», «Дифференциальное исчисление, «Предельный анализ в экономике»; задания для самостоятельного решения, примеры выполнения заданий, список литературы. Методическое пособие предназначено для студентов 1 курса Международного института рынка, изучающих математику по направлениям «Экономика», «Менеджмент», а также по специальностям «Менеджмент организации», «Маркетинг», «Прикладная информатика в экономике», «Финансы и кредит», «Экономика и управление на предприятии».
Составители Лищинская Евгения Эльявна старший преподаватель, Коваленко Татьяна Дмитриевна к.т.н., доцент, Лищинский Наум Яковлевич к.т.н., доцент.
Печатается по решению Научно-методического совета Международного института рынка
Ó Международный институт рынка, 2008
СОДЕРЖАНИЕ
1. элементарные функции Линейная функция y=kx+b Рассмотрим частные случаи. Если k=0, имеем у=b. Значение у не зависит от х и при любом значении х принимает постоянное значение b. Графиком этой функции является прямая, параллельная оси Ох и пересекающая ось Оу в точке у = b (рис. 1.1). Если b = 0 и k ≠ 0, имеем у = kx. Такую функцию называют прямой пропорциональной зависимостью. Ее графиком является прямая, проходящая через начало координатной плоскости — точку О (рис. 1.2). Число k называют угловым коэффициентом прямой, который определяет тангенс угла ее наклона к положительной полуоси абсцисс (k = tg a). Если k > 0 угол α острый, и функция возрастает на всей области определения; при k < 0 угол α тупой, функция убывает. Для построения графика используют точку О (0; 0) и любую точку прямой М (х; kx), через которые проводят прямую линию.
Рис. 1.1 Рис. 1.2
Графиком функции у = kx + b (рис. 1.2) является прямая, полученная параллельным переносом прямой у = kx на | b | единиц вдоль оси ординат вверх, если b > 0, или вниз, при b < 0.
Для построения графика достаточно найти любые две точки прямой, через которые и проводят линию.
Замечание. Легко построить график линейной функции, если уравнение прямой задано в виде
Пример 1.1. Построить график функции у=2х+6.
РЕШЕНИЕ:График этой функции есть прямая. Построим ее. 1-й способ. Выберем произвольно две точки прямой. Например, если х = 0, то y= 2·0 + 6 = 6. Координаты первой точки (0; 6). Если х = -2, то у = 2 ·(-2) + 6 = 2. Вторая точка (-2; 2). Отметим их на координатной плоскости, проведем через них прямую (рис. 1.4). 2-й способ. Преобразуем уравнение прямой к уравнению в отрезках: -2х+у=6, Получили, что искомая прямая пересекает ось Ох в точке х =-3, а ось Оу — в точке y =6. Проведем через эти точки прямую (рис. 1.5).
Рис. 1.4. Рис.1.5
Дробно-линейная функция Рассмотрим частный случай: Область определения — вся числовая прямая, кроме х = 0: D(y) = (- Функция нечетная: Графиком обратной пропорциональности является гипербола (рис. 1.6), которая состоит их двух ветвей и симметрична относительно начала координат. Если k > 0 ветви гиперболы расположены в I и III координатных четвертях; при k < 0 — во II и IV четвертях.
Рис. 1.6. Рис. 1.7. Для более точного построения гиперболы отметим на координатной плоскости несколько точек одной из ее ветвей. Вторая ветвь есть симметричное отображение первой относительно начала координат. Функцию Пример 1.2. Построить график функции
РЕШЕНИЕ:
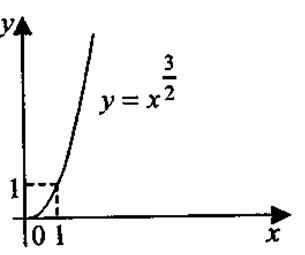
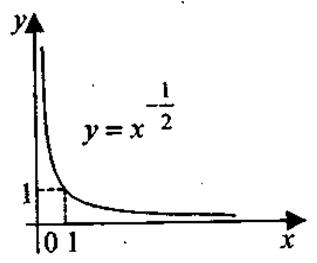
Получили Построим гиперболу Квадратичная функция у=ах2 + bх + с, a Свойства функции 1. Область определения степенной функции — множество всех положительных чисел: х >0 (при х ≤ 0 выражение ха имеет смысл не для всех а 2. Множество значений степенной функции — множество всех положительных чисел: у > 0. 3. Степенная функция является функцией общего вида. 4. График функции проходит через точку с координатами (1; 1). При а >0 график функции проходит через начало координат О (0; 0). 5. Если а >0, функция возрастает во всей области определения; при а <0 — убывает. На рис. 1.12 представлены примеры графиков степенной функции.
Рис. 1.12. Показательная функция у = аx, где а > 0, а Свойства функции 1. Область определения показательной функции — вся числовая прямая: х 2. Множество значений— вся положительная полуось: у > 0. 3. Показательная функция является функцией общего вида. 4. График функции проходит через точку с координатами (0; 1). 5. Если а> 1,функция возрастает во всей области определения; при 0 < а < 1 — убывает. На рис. 1.13 представлены примеры графиков показательной функции.
Логарифмическая функция у = loga x, где а > 0, а Свойства функции 1. Область определения логарифмической функции – положительная полуось: х >0. 2. Множество значений - вся числовая прямая: y 3. Логарифмическая функция является функцией общего вида. 4. График функции проходит через точку с координатами (1; 0). 5. Если а > 1, логарифмическая функция возрастает во всей области определения; при 0 < а < 1 — убывает. На рис. 1.14 представлены графики логарифмической функции.
Преобразование графика функции 1. Смещение графика параллельно оси ординат График функции у = f(x) + а получается из графика функции у = f(x) параллельным смещением его на | а | единиц по оси Оу вверх, если а >0, или вниз, при а < 0 (рис. 1.15).
Рис. 1.15
2. Смещение графика параллельно оси абсцисс График функции у = f(x - а) получается из графика функции у = f(x) его параллельным смещением вдоль оси Ох на |а | единиц вправо, если а > 0, или влево, при а <0 (рис. 1.16).


Рис. 1.16.
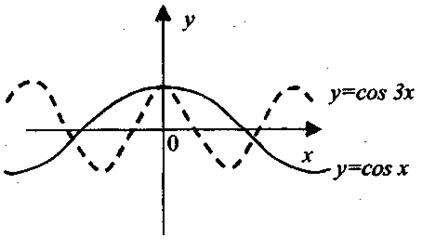
3. Сжатие и растяжение графика функции График функции у = kf(x), где k > 0 получается из графика функции у = f(x) путем его сжатия, если 0<k < 1, или растяжения, при k > 1от оси абсцисс в k раз (рис 1.17). График функции у = f(kx), где k > 0 получается из графика функции у = f(x) путем его сжатия, если k > 1 к оси ординат в k раз, или растяжения, если 0 < k < 1 от оси ординат в 1/ k раз. Например, график функции у = cos 3 x получается из графика функции у = cos x сжатием к оси ординат в 3 раза (рис. 1.18).
Рис. 1.17.
Рис. 1.18
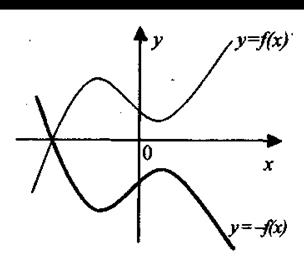
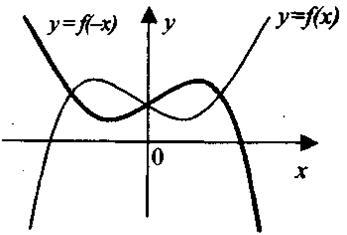
4. Симметричное отображение относительно координатных осей. График функции у = - f(x) получается из графика функции у = f(x) симметричным отображением относительно оси абсцисс (рис 1.19). График функции у = f(-x) получается из графика функции у = f(x) симметричным отображением относительно оси ординат (рис 1.20).
Рис. 1.19. Рис. 1.20.
График функции График функции
Рис. 1.21.
Задания для самостоятельной работы
Постройте график функции
ПРЕДЕЛЫ И НЕПРЕРЫВНОСТЬ Примеры. 1.
2.
3.
Или
Пример. Найти РЕШЕНИЕ
Ответ данной задачи будем использовать далее как заранее известный факт. 2.2.1. Раскрытие неопределенности типа В случае степенных функций необходимо выносить за скобку в числителе и знаменателе дроби x с наибольшим показателем степени среди всех слагаемых дроби; в случае показательных функций за скобку выносится наиболее быстро возрастающее слагаемое, среди всех слагаемых дроби. После сокращения дроби неопределенность устраняется. Пример.
Задания для самостоятельной работы
2.2.2. Раскрытие неопределенности типа В этом случае обычно используются следующие приемы: a) алгебраические преобразования числителя и знаменателя дроби, приводящие к формулам сокращенного умножения; неопределенность устраняется после сокращения дроби; b) вынесение в числителе и знаменателе дроби степени х с наименьшим показателем; c) Деление числителя дроби на ее знаменатель; d) Эквивалентность бесконечно малых величин; e) Первый замечательный предел. Примеры. a)
(дополнили числитель до разности квадратов b) c)
d) Примеры эквивалентных бесконечно малых величин при
Предел отношения двух бесконечно малых величин не изменится, если эти бесконечно малые величины заменить им эквивалентными. Пример.
e)
Примеры. 1)
2)
2.2.3. Раскрытие неопределенности типа В этом случае выражение, стояще под знаком предела представляет собой степенно-показательную функцию, в основании которой необходимо выделить целую часть дроби (которая должна быть равна 1). Неопределенность устраняется при помощи «второго замечательного предела». 1)
Примеры 1) 2)
3)
2.2.4. Раскрытие неопределенности типа Если функция, стоящая под знаком предела представляет собой алгебраическую сумму дробей, то неопределенность устраняется или приводится к неопределенности Примеры. 1)
2)
Задания для самостоятельной работы
Правила дифференцирования 1. 2. 3. 4.
Примеры.
Найти производную функции, пользуясь определением.
1) 2) 3) 4) 5) 6) х0 – произвольно выбранная точка. х=0 – только правостороннюю производную.
7) 8) 9) 10) 12)
Таблица производных
Примеры. Найти производные функций 1) 4)
Решение:
1)
2)
3)
4)
5)
Задания для самостоятельной работы
Найти производные функций
ПРИЛОЖЕНИЕ ПРОИЗВОДНОЙ. Правило Лопиталя (для неопределенностей вида Предел отношения функций равен пределу отношения производных этих функций, если предел отношения производных существует. Примеры. 1.
2.
3.
4.
5.
Раскрытие неопределенностей вида Вычисление пределов функций можно осуществлять при помощи преобразования
В силу непрерывности показательной функции:
Пример
Задания для самостоятельной работы 1)
3)
5)
Справочный материал. Определение 1. Функция
Определение 2. Функция Возрастающие и убывающие функции называются монотонными, а промежутки, в которых функция возрастает или убывает,- промежутками монотонности. Возрастание и убывание функции
Определение 3. Внутренние точки области определения функции Производная Теперь мы можем сформулировать ПРАВИЛО нахождения интервалов монотонности функции 1. Находим область определения функции 2. Вычисляем производную 3. Критическими точками и точками разрыва функции разбиваем область определения функции 4. Исследуем знак Пример 4.1. Найти интервалы монотонности функции
РЕШЕНИЕ: 1. 2. Найдём критические точки | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |


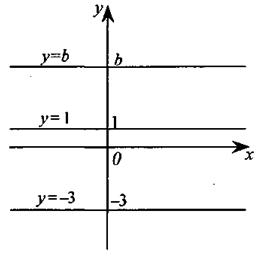

 Рис. 1.3
Рис. 1.3

 (говорят: «уравнение в отрезках»), где числа а и b определяют точки пересечения прямой с осью абсцисс и ординат соответственно (рис. 1.3).
(говорят: «уравнение в отрезках»), где числа а и b определяют точки пересечения прямой с осью абсцисс и ординат соответственно (рис. 1.3).
 ,
, 




 ; 0)
; 0)  (0;
(0; 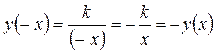


 легко преобразовать к виду
легко преобразовать к виду  , например, делением числителя на знаменатель. График дробно-линейной функции (рис. 1.7) получается путем параллельного переноса гиперболы
, например, делением числителя на знаменатель. График дробно-линейной функции (рис. 1.7) получается путем параллельного переноса гиперболы  на
на  единиц вдоль оси абсцисс (влево, если п > О, или вправо, если п < 0) и на
единиц вдоль оси абсцисс (влево, если п > О, или вправо, если п < 0) и на  единиц вдоль оси ординат (вверх, если m >0, или вниз, при m < 0).
единиц вдоль оси ординат (вверх, если m >0, или вниз, при m < 0).
 Выделим целую часть.
Выделим целую часть.  6х-5 2х-3
6х-5 2х-3 6х-9 3
6х-9 3 4
4 Рис. 1.8
Рис. 1.8 .
. для этого используем принадлежащие ей точки (1; 2), (2; 1), (0,5; 4), (4; 0,5). График исходной функции получим, сдвинув гиперболу
для этого используем принадлежащие ей точки (1; 2), (2; 1), (0,5; 4), (4; 0,5). График исходной функции получим, сдвинув гиперболу 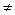 0
0 R).
R).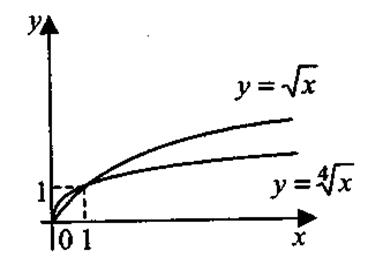
 R.
R. Рис. 1.13.
Рис. 1.13. Рис. 1.14.
Рис. 1.14.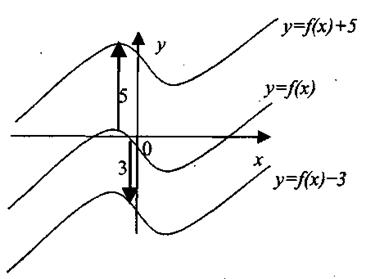

 получается из графика функции у = f(x) симметричным отображением относительно оси Ох той части графика, которая лежит ниже оси абсцисс (рис 1.21).
получается из графика функции у = f(x) симметричным отображением относительно оси Ох той части графика, которая лежит ниже оси абсцисс (рис 1.21).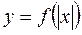 получается из графика функции у = f(x) симметричным отображением относительно оси О у той части графика, которая лежит справа от оси ординат О у (рис 1.22).
получается из графика функции у = f(x) симметричным отображением относительно оси О у той части графика, которая лежит справа от оси ординат О у (рис 1.22).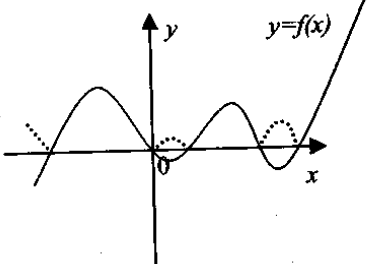

 Рис. 1.22
Рис. 1.22

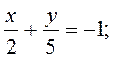
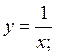
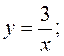
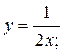 ;
;



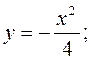
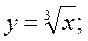
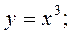
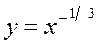 ;
;
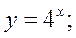
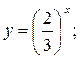
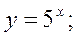
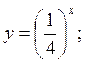


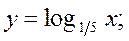
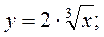

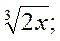
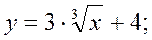
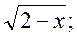 ;
;
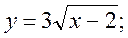
 ;
;


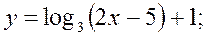
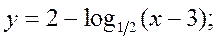


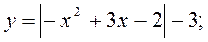

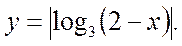

 т.к.
т.к.  при
при  является б.б.в., то
является б.б.в., то  при
при  по определению бесконечно малой величины. Или
по определению бесконечно малой величины. Или  ;
; т.к.
т.к.  при
при  является бесконечно малой величиной, тогда
является бесконечно малой величиной, тогда 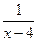 -бесконечно большая величина;
-бесконечно большая величина; 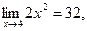 т.е. функция
т.е. функция  является бесконечно большой величиной, т.е.
является бесконечно большой величиной, т.е.  по определению бесконечно большой величины.
по определению бесконечно большой величины.

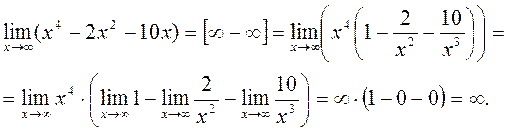
 .
.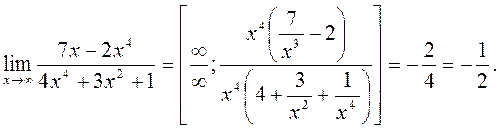
 3)
3) 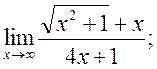
 4)
4) 
 .
.


 , а знаменатель до разности кубов
, а знаменатель до разности кубов  ).
).


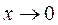 :
:


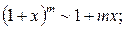




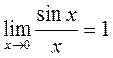 - первый замечательный предел.
- первый замечательный предел.

 .
. ; 2)
; 2) 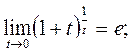





 после приведения дробей к общему знаменателю. Если функция представляет собой сумму иррациональных выражений, то неопределенность или устраняется, или приводится к виду
после приведения дробей к общему знаменателю. Если функция представляет собой сумму иррациональных выражений, то неопределенность или устраняется, или приводится к виду  путем домножения и деления функции на одно и то же (сопряженное выражение), приводящее к формулам сокращенного умножения.
путем домножения и деления функции на одно и то же (сопряженное выражение), приводящее к формулам сокращенного умножения.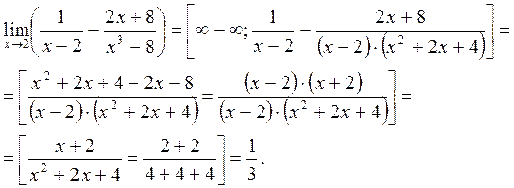


 4)
4) 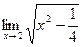 7)
7)  10)
10)  13)
13)  16)
16)  19)
19)  22)
22) 
 5)
5)  8)
8)  11)
11)  14)
14)  17)
17) 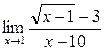 20)
20)  23)
23) 
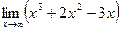 6)
6)  9)
9)  12)
12) 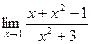 15)
15)  18)
18)  21)
21)  24)
24) 
 28)
28) 
 29)
29) 
 30)
30) 




 , х>0
, х>0 ,
, 
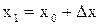 ,
, 



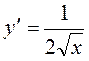 для х>0, т.к.
для х>0, т.к.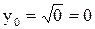
 ,
, 
 .
. 11)
11)  .
. .
. существует, но функция не дифференцируется, т.е. не имеет конечной производной.
существует, но функция не дифференцируется, т.е. не имеет конечной производной. где c-константа
где c-константа








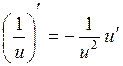



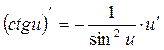


 2)
2)  3)
3) 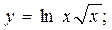
 5)
5) 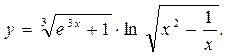

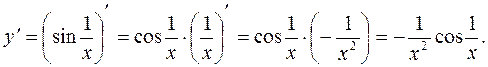



 2)
2)  3)
3)  4)
4) 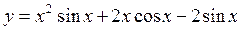 5)
5) 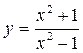 6)
6)  7)
7)  8)
8)  9)
9) 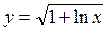 10)
10)  11)
11)  12)
12)  13)
13)  14)
14)  15)
15) 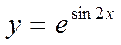 16)
16) 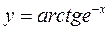 17)
17)  18)
18) 
 20)
20)  21)
21) 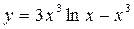 22)
22)  23)
23)  24)
24)  25)
25) 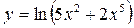 26)
26)  27)
27) 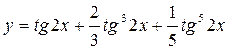 28)
28)  29)
29)  30)
30) 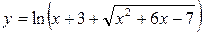 31)
31)  32)
32)  33)
33)  34)
34) 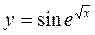 35)
35)  36)
36) 
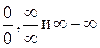 )
)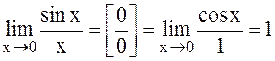







 ,
,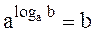 - логарифмическое тождество.
- логарифмическое тождество.

 2)
2) 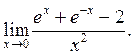
 4)
4) 
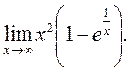 6)
6) 
 называется возрастающей на множестве
называется возрастающей на множестве 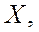 если для любых
если для любых  и
и  выполняется условие
выполняется условие 
 называется убывающей на множестве
называется убывающей на множестве  если для любых
если для любых  из
из 
 для всех x из
для всех x из  то
то  для всех
для всех  то
то  равна 0 или не существует, называются критическими точками этой функции.
равна 0 или не существует, называются критическими точками этой функции.
 на интервалы, на каждом из которых производная сохраняет знак, т.е. интервалы знакопостоянства
на интервалы, на каждом из которых производная сохраняет знак, т.е. интервалы знакопостоянства 
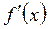 на каждом из интервалов знакопостоянства. Если на рассматриваемом интервале
на каждом из интервалов знакопостоянства. Если на рассматриваемом интервале  то на этом интервале
то на этом интервале  возрастает, если же
возрастает, если же  то на этом интервале
то на этом интервале