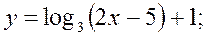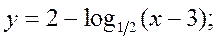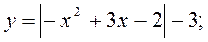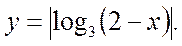Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства квадратичной функцииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
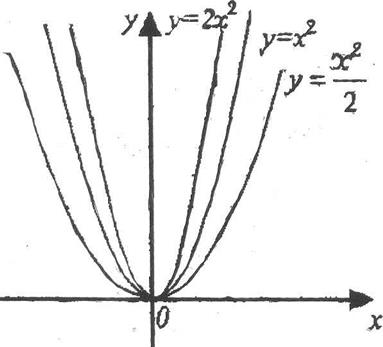
1. Область определения — вся числовая ось, то есть 2. Если b= 0, функция у = ах2 + с является четной. При b общего вида, то есть не является ни четной, ни нечетной. 3. Графиком функции является парабола. 4. Функция имеет единственную критическую точку х0 является точкой минимума, а <0 — точкой максимума. 5. Точку с координатами (х0; у0), где Рассмотрим частные случаи. 1. Функция у = х2. Ее графиком является парабола, ветви которой направлены вверх и симметричны относительно оси ординат. Вершина этой параболы находится в начале координат. Строим график параболы (рис. 1.9), для точности построения используем точки (1; 1), (2; 4), (3; 9), принадлежащие ее правой ветви. Левую ветвь получим симметричным отображением правой относительно оси ординат.
Рис. 1.9.
2. Функция у = ах2. Вершина параболы совпадает с, началом координатной плоскости О (0; 0). Коэффициент а определяет: 1) направление ветвей параболы вверх (а >0) или вниз (а <0); 2) растяжение (при | а | <1) от оси абсцисс или сжатие (при а > 1) к оси абсцисс в а раз (см. рис. 1.9).
Рис. 1.10.
График функции у = ах2 + bх + с получается из графика функции у = ах2 путем его параллельного переноса сначала вдоль оси ОХ на Другими словами для построения графика функции у = ах2 + bх + с на координатной плоскости отмечаем вершину параболы А (х 0; у 0).Параллельным переносом смещаем координатные оси так, чтобы начало координат совпало с точкой А. Относительно новой координатной плоскости строим график функции у = ах2. Пример 1.3. Построить график функции
РЕШЕНИЕ:
Найдем координаты вершины параболы a(x0; y0):
Параллельным переносом смещаем координатные оси так, чтобы начало координат совпало с точкой А(1;-3). Относительно новой координатной плоскости строим график функции у = -2х2 (рис. 1.11).
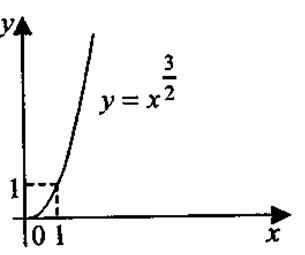
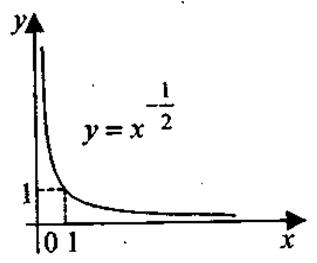
Степенная функция у = ха, где а Свойства функции 1. Область определения степенной функции — множество всех положительных чисел: х >0 (при х ≤ 0 выражение ха имеет смысл не для всех а 2. Множество значений степенной функции — множество всех положительных чисел: у > 0. 3. Степенная функция является функцией общего вида. 4. График функции проходит через точку с координатами (1; 1). При а >0 график функции проходит через начало координат О (0; 0). 5. Если а >0, функция возрастает во всей области определения; при а <0 — убывает. На рис. 1.12 представлены примеры графиков степенной функции.
Рис. 1.12. Показательная функция у = аx, где а > 0, а Свойства функции 1. Область определения показательной функции — вся числовая прямая: х 2. Множество значений— вся положительная полуось: у > 0. 3. Показательная функция является функцией общего вида. 4. График функции проходит через точку с координатами (0; 1). 5. Если а> 1,функция возрастает во всей области определения; при 0 < а < 1 — убывает. На рис. 1.13 представлены примеры графиков показательной функции.
Логарифмическая функция у = loga x, где а > 0, а Свойства функции 1. Область определения логарифмической функции – положительная полуось: х >0. 2. Множество значений - вся числовая прямая: y 3. Логарифмическая функция является функцией общего вида. 4. График функции проходит через точку с координатами (1; 0). 5. Если а > 1, логарифмическая функция возрастает во всей области определения; при 0 < а < 1 — убывает. На рис. 1.14 представлены графики логарифмической функции.
Преобразование графика функции 1. Смещение графика параллельно оси ординат График функции у = f(x) + а получается из графика функции у = f(x) параллельным смещением его на | а | единиц по оси Оу вверх, если а >0, или вниз, при а < 0 (рис. 1.15).
Рис. 1.15
2. Смещение графика параллельно оси абсцисс График функции у = f(x - а) получается из графика функции у = f(x) его параллельным смещением вдоль оси Ох на |а | единиц вправо, если а > 0, или влево, при а <0 (рис. 1.16).


Рис. 1.16.
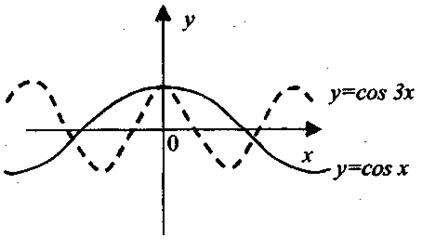
3. Сжатие и растяжение графика функции График функции у = kf(x), где k > 0 получается из графика функции у = f(x) путем его сжатия, если 0<k < 1, или растяжения, при k > 1от оси абсцисс в k раз (рис 1.17). График функции у = f(kx), где k > 0 получается из графика функции у = f(x) путем его сжатия, если k > 1 к оси ординат в k раз, или растяжения, если 0 < k < 1 от оси ординат в 1/ k раз. Например, график функции у = cos 3 x получается из графика функции у = cos x сжатием к оси ординат в 3 раза (рис. 1.18).
Рис. 1.17.
Рис. 1.18
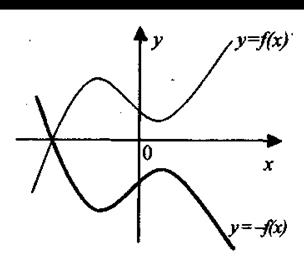
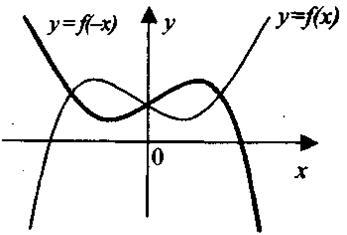
4. Симметричное отображение относительно координатных осей. График функции у = - f(x) получается из графика функции у = f(x) симметричным отображением относительно оси абсцисс (рис 1.19). График функции у = f(-x) получается из графика функции у = f(x) симметричным отображением относительно оси ординат (рис 1.20).
Рис. 1.19. Рис. 1.20.
График функции График функции
Рис. 1.21.
Задания для самостоятельной работы
Постройте график функции
ПРЕДЕЛЫ И НЕПРЕРЫВНОСТЬ
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 666; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.151.112 (0.006 с.) |

 .
.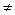 0 - функция
0 - функция , при а > 0
, при а > 0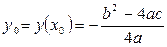 называют вершиной параболы. Квадратичная парабола симметрична относительно прямой х = х0. При построении графика достаточно отметить точки, через которые проходит одна из ветвей параболы. Вторая ветвь получается путем симметричного отображения первой относительно прямой
называют вершиной параболы. Квадратичная парабола симметрична относительно прямой х = х0. При построении графика достаточно отметить точки, через которые проходит одна из ветвей параболы. Вторая ветвь получается путем симметричного отображения первой относительно прямой 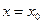

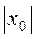 единиц вправо, если абсцисса вершины параболы x0> 0, или влево при x0< 0; затем вдоль оси Оу на
единиц вправо, если абсцисса вершины параболы x0> 0, или влево при x0< 0; затем вдоль оси Оу на 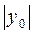 единиц вверх, если ордината вершины параболы у0 >0, или вниз при y <0 (рис. 1.10).
единиц вверх, если ордината вершины параболы у0 >0, или вниз при y <0 (рис. 1.10).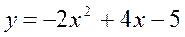
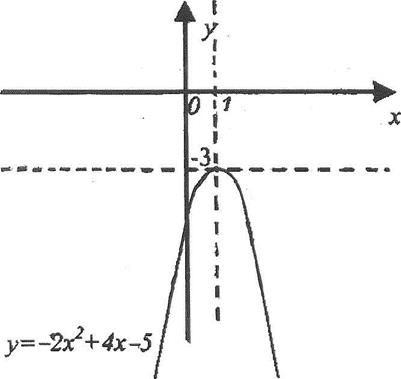 Рис. 1.11
Рис. 1.11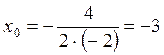
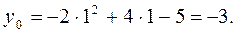
 R
R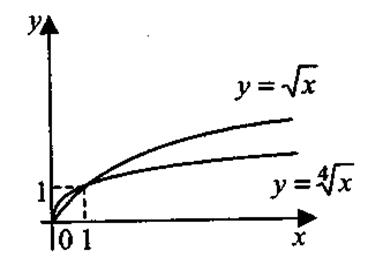
 R.
R. Рис. 1.13.
Рис. 1.13. Рис. 1.14.
Рис. 1.14.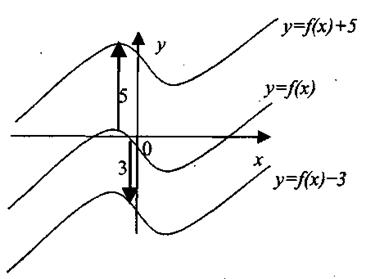

 получается из графика функции у = f(x) симметричным отображением относительно оси Ох той части графика, которая лежит ниже оси абсцисс (рис 1.21).
получается из графика функции у = f(x) симметричным отображением относительно оси Ох той части графика, которая лежит ниже оси абсцисс (рис 1.21).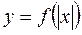 получается из графика функции у = f(x) симметричным отображением относительно оси О у той части графика, которая лежит справа от оси ординат О у (рис 1.22).
получается из графика функции у = f(x) симметричным отображением относительно оси О у той части графика, которая лежит справа от оси ординат О у (рис 1.22).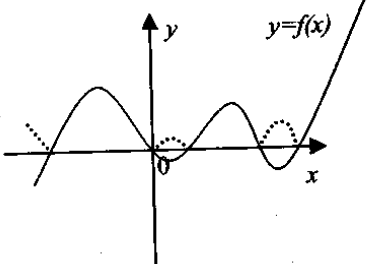

 Рис. 1.22
Рис. 1.22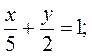

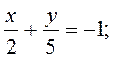
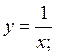
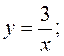
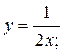 ;
;



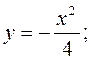
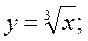
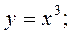
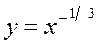 ;
;
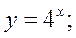
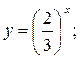
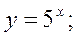
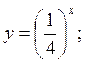


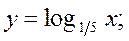
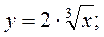

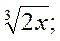
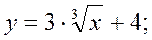
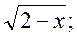 ;
;
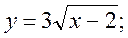
 ;
;