
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод дендритов: вроцлавская таксономияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Метод вроцлавской таксономии часто называют методом дендритов. Авторы этого метода определяют дендрит как ломаную, «... которая может разветвляться, но не может содержать замкнутых ломаных, и такая, что любые две точки множества 2 ею соединены» [4]. Этим методом получают нелинейное упорядочение изучаемых единиц, что, с одной стороны, полнее характеризует действительность, но, с другой стороны, создает больше трудностей при интерпретации. Нелинейное упорядочение характеризуется отсутствием явной иерархии, выражающимся в том, что некоторые единицы могут быть связаны с большим числом других единиц (например, с пятью). В этом случае отсутствует четко определяемый порядок, не известно, какой элемент является предшествующим, а какой последующим. Рассматриваемые случаи упорядочения можно представить графически н виде точек или кружков (со вписанными в них обозначениями единиц), связанных отрезками. Точки, изображающие единицы, чаще всего называют вершинами, а отрезки - связями (дугами). Упомянутые линейный и нелинейный способы упорядочения иллюстрируют рисунки 2.1 и 2.2.
Представленные на рисунках упорядочения, очевидно, не исчерпывают все возможные ситуации. В связи с этим возникает задача выбора наилучшего упорядочения, заключающаяся в нахождении такого дендрита, в котором смежные единицы будут иметь наименее различающиеся значения признаков. Выполнение этого условия приведет к упорядочению с наименьшими расстояниями между отдельными элементами. в оптимальном дендрите - с наименьшей суммой длин связей - смежные объекты в наименьшей степени отличаются друг от друга Поэтому при сравнении различных упорядочений объектов и выборе наилучшего упорядочения исходят из длины связей дендрита. Построение оптимального дендрита заключается в установлении связей между единицами, наименее отличающимися друг от друга с этой целью из составленной матрицы расстояний выбирают единицы с близкими значениями признаков. Поиск таких единиц проводится путем нахождения наименьших чисел в каждом столбце (или строке) матрицы Искомые ближайшие единицы обозначены номерами строк, т столбцов), в которых находятся наименьшие числа. Если, например надо найти единицу, наименее отличающуюся от j, то достаточно отыскать наименьшее число в столбце j. Пусть этим числом будет элемент находящийся в строке і. Тогда ближайшей к единице j будет единица і. Данный пример выбора ближайшего элемента иллюстрирует таблица 2.1.
Предложенный авторами вроцлавской таксономии способ построения оптимального дендрита состоит из нескольких этапов. На первом этапе устанавливаются связи каждой из исследуемых единиц с ближайшими единицами. Для удобства описания выполняемых операций предположим, что у пас имеется множество единиц, обозначенных символами 1, 2, 3, 4, 5, 6, 7, К, 9. Далее предположим, что в этом множестве из девяти элементов получены следующие сочетания ближайших единиц (рисунок 2.3).
Нетрудно заметить, что некоторые связи встречаются дважды, например 1-3 и 3-1 (т.е. к единице 1 ближе всего находится единица 3, а к единице 3 ближе всего расположена единица 1). Поскольку при построении дендрита очередность установления связей не играет роли, одно из повторяющихся сочетаний всегда исключается. Подобное исключение проводится для всех выделенных пар связей. Это приводит к тому, что остаются связи 2-7 и 8-9, а связи 7-2 и 9-8 отбрасываются. Для оставшихся двух связей характерно наличие единицы, обозначенной номером 5, поэтому связи 4-5 и 5-6 можно объединить в один общий набор. В результате получаются четыре отдельные конструкции, называемые скоплениями 1-го порядка (рисунок 2.4).
Полученные скопления не удовлетворяют основному условию дендрита, а именно они не связаны в единое целое. Для выполнения этого требования выбирается наименьшее расстояние между единицами, входящими в различные скопления 1-го порядка. Соответствующий отрезок становится связью между двумя скоплениями. В результате получаются скопления 2-го порядка. Если эти скопления также оказываются изолированными, то вышеупомянутая операция повторяется, что приводит к получению скопления 3-го, а затем и высших порядков. Процесс построения дендрита заканчивается, когда любые две точки исследуемого множества оказываются связанными друг с другом. Очередная процедура, которую надлежит теперь выполнить, заключается в нахождении наименьшего расстояния каждой единицы одного скопления от единиц остальных скоплений. Затем их этих расстояний выбирается наименьшее, которое становится связью, соединяющей отдельные скопления. Предположим, что искомыми оказались расстояния между единицами 5 и 3, а также единицами 2 и 8 (рисунок 2.5).
Нахождение наименьшего расстояния между скоплениями 2-го порядка и объединение их в одно общее целое - последняя операция в рассматриваемом примере, которой завершается процедура построения дендрита. Предположим, что искомой связью оказалась связь между единицами 5 и 8, тогда дендрит девятиэлементного множества выглядит так, как показано на рисунке 2.6.
Метод «центра тяжести» Способ выбора репрезентантов по этому методу зависит от размера I руппы. Различаются группы из одного, из двух элементов, а также группы большей численностью элементов [4]. В группах из одного элемента образующие их единицы обладают шачениями признаков, сильно отличающимися от остальных. Таким образом, их относят к числу элементов-эталонов (репрезентантов). С группами, где число элементов больше двух, поступают следующим образом. Рассчитываются расстояния каждой единицы от остальных единиц данной группы (2.16):
В набор элементов-эталонов входит единица с наименьшей суммой расстояний (2.17):
Заключительный этап процедуры состоит в выборе репрезентантов из группы с двумя элементами. С этой целью рассчитывается сумма
2к - число элементов в к группах из двух элементов; р - число обособленных элементов и элементов-эталонов, выбранных из групп с числом элементов больше двух. Репрезентантом каждой из этих групп является тот элемент, у которого больше сумма расстояний от обособленных элементов и элементов- эталонов, выделенных из групп с числом элементов больше двух (2.19):
По выполнении указанных операций получается набор элементов- эталонов, представляющих каждую из выделенных групп. Выбранные элементы находятся вблизи «центра тяжести» группы и поэтому обладают «средними» значениями характеризующих их признаков. 2.2.5 Таксономический метод оценивания качества машиностроительной продукции на основе рангово- классификационной шкалы Таксономический метод построения классификационной шкалы в ранговом пространстве мер качества проектов и оценку качества проектов на основе рангово-классификационной шкалы можно применять по отношению к разработкам любых технологий и объектов техники. Алгоритм оценки включает в себя несколько этапов [1]. Во-первых, осуществляется дифференциальное ранговое шкалирование проектов-аналогов по каждому оценочному показателю на множестве проектов-аналогов, т.е. строятся ранжировки показателей. Полученная ранжировка проектов-аналогов представляется в виде матрицы рангов. Матрица рангов переводится в булеву матрицу на основе предиката Р,. Смысл операции - перевести матрицу рангов в (1;0) - матрицу, где единицу получают ранги, превысившие 50 % максимального ранга.
Выполняется операционное свертывание предикатов Р, по каждому проекту-аналогу по основным оценочным показателям (2.20):
где k - число образцов-аналогов. Дискриминатор делит проекты на две группы — проектов, для которых доля «хороших» оценочных показателей приблизительно больше 40-45 %, и проектов, для которых эта доля меньше. Формируется эталон и категория качества (2.22):
Как следует из формул, ранговые эталоны означают следующие ранги по каждому из оценочных показателей: категория 1 - лучшие ранги в нервом ранговом классе К1 категория 2 - средние ранги в К1 категория 3 средние ранги во втором ранговом классе К2; категория 4 - худшие ранги в К2. Полученные категории качества в рангах показателей и есть рангово- классификационная шкала качества на множестве выбранных проектов- аналогов. Каждый показатель качества оцениваемого проекта сравнивается со шачениями показателей проектов-аналогов с учетом построенной ранговой шкалы предпочтения. Определяются ранги показателей оцениваемого качества проектов. Ранги оцениваемого качества проекта сравниваются с ранговыми категориями Kat.1,Kat.2,Kat.3,Kat.4; с помощью мер сходства в ранговой шкале. Проекту присваивается оценка качества - та категория, с вектором рангов которой обеспечено наибольшее сходство.
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 705; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.223.12 (0.011 с.) |

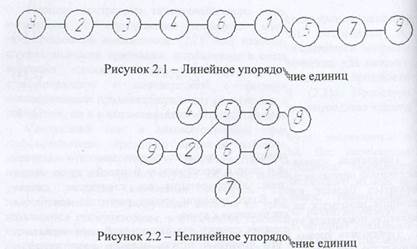

 Рисунок 2.3 - Сочетания ближайших единиц
Рисунок 2.3 - Сочетания ближайших единиц
 Рисунок 2.4 - Скопления 1-го порядка
Рисунок 2.4 - Скопления 1-го порядка
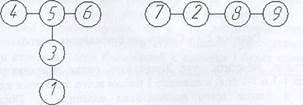 Рисунок 2.5 - Скопления 2-го порядка
Рисунок 2.5 - Скопления 2-го порядка
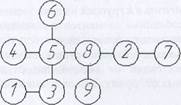 Рисунок 2.6 - Дендрит, построенный на единицах исследуемого множества
Рисунок 2.6 - Дендрит, построенный на единицах исследуемого множества












