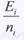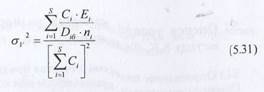Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценка уровня качества разнородной продукции по методу А.В. ГличеваСодержание книги
Поиск на нашем сайте
5.2.1 Определение индексов качества продукции При оценке уровня качества разнородной продукции, так же как и при комплексной оценке качества продукции одного вида, основным является средний взвешенный индекс качества, определяемый по формуле [6]:
значение относительного показателя качества к-го вида продукции
где - значение единичного или комплексного показателя качества к-го
где Ск - ооъем производства продукции к-го вида в денежном выражении. Для штучной продукции
где - количество изделий к-го вида продукции; °к - затраты на создание и эксплуатацию изделия к-го вида продукции; М - число различных видов продукции. Коэффициенты весомости соответствуют плановым заданиям и характеризуют плановое распределение общих затрат
Величины являются оптимальными потребностей народного хозяйства.С точки зрения Если в ходе выполнения плана целесообразна количество выпускаемой предприятием продукции скорректировать отвечающее им распределение затрат, то величины ак (/ каждого вида и = 1,..., М) должны соответствовать исправленным плановым заданиям. Для упрощения расчетов вместо средн^ погрешности е^ от замены средних взвешеннькне относительнои \ расчет которой приводится ниже. р Средний взвешенный арифметический индекс качес\ формуле Ьва вычисляется по
где <=>*, ак — определяются соответственно по формул^ Индексы качества продукции, определенные д^ (5.9) и (5.10). управления, позволяют построить систему показателе^1 Разных звеньев общими интересами народного хозяйства. Исходны.' согласованнУю с системе является предприятие. ^ звеном в такой 5.2.2 Определение индексов дефектности продук^ Для определения показателя дефектности берется |>1И единиц продукции. Обозначим через т1 число дефекто(1ыбоРка объемом п вида. Тогда показатель дефектности находим по уравне' (недостатков) 1-го ШЮ [6]
где с! — число всех видов дефектов и недостатков данной продукции. * встречающихся у Если за базовый период проверено N изделий и дефектов (недостатков) 1-го вида (1 =1,2,...,(1), то (\У них найдено М(дефектности находим по уравнению 'азовый показатель
где
Если величина п мала (по сравнению с Ы), то даже при стабильном качестве изготовления продукции будет наблюдаться рассеивание выборочного показателя дефектности Об.
Если величина р; невелика по сравнению с единицей, то, как правило, можно считать, что распределение величин подчиняется закону Пуассона. При этом для математического ожидания и дисперсии будем иметь Из уравнений (5.22) и (5.23) следует, что величина Е определяется по характеристикам базового периода. При помощи уравнений (5.17) и (5.21) можно построить контрольную карту для показателя дефектности (рисунок 5.1). Центральная линия проводится на уровне 06, а верхняя и нижняя контрольные границы находятся по уравнениям
где
Откладывая величину D для последовательных выборок на контрольной карте, можно следить за динамикой изменения дефективности. Для этой цели необходимо рационально выбрат^ения Дефектности. Дело в том, что при малом объеме п будет велико рассеивание выборки n7 контрольной карте даже при стабильном качестве Ссеивание точек 1|а большом п определение показателя дефектности стано 3готовления, а при Можно рекомендовать для выбора п такое тРУД°емким. ^ квадратическое отклонение показателя дефектност.'Ичение среднее уравнению (5.22), не должно превышать 10 % от ^ определяемое по дефектности, определяемого по уравнению (5.21). Нового показателя Отсюда получим уравнение для минимального объ
Отсюда видно, что коэффициент влияния 2, показывает долю, которую составляет дефект (недостаток) 1-го вида в показателе дефектности. Очевидно, что для снижения показателя дефектности нужно в первую очередь добиваться устранения тех дефектов (недостатков), у которых коэффициент влияния наибольший. Рассмотрим теперь вопрос об индексе дефектности. Пусть имеются 8 видов продукции, для которых определены в рассматриваемый период показатели дефектности Оь Эг,...,Оя и соответствующие базовые
Введем относительные показатели дефектности
где 1=1, 2,...,8. Тогда индекс дефектности продукции для рассматриваемого периода определим по уравнению
где С, — сумма, на которую изготовлено продукции 1-го вида в рассматриваемом периоде (1= 1, 2,..., 8). Из уравнения (5.11) можно получить выражение для дисперсии индекса дефектности, аналогичное уравнению (5.20).
Подставляя вместо СГг величину п (см. уравнение (5.22)), получим
Доверительные границы для индекса ^ находя1(Я „о уравнению (5.24) и (5.25), если в них ™С™(кроме кв,„тиля У а, которая остается без изменения).
Покажем это в общем виде для случая, коц^ отсюда следует, что с ростом величины ошибка определения индекса дефектности 5 уменьшается случайная информации, получаемой по выборкам ограни зависящая от неполноты Использование индексов дефектности ЧенНого объема, качества выпускаемой продукции целесооб^°дУКЦии как показателя оценке деятельности отдельных пронзц^ °> главным образом, при предприятия (цехов, участков). Индекс дефе^ Генных подразделений и оценить качество различных видов изделий Г,'0Сти позволит сопоставить определения качества труда, стабильности ^Угри предприятия в целях влияющих на качество продукции, и т. д. ^Тва, основных факторов,
|
|||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 349; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.29.98 (0.006 с.) |





 вида продукции; IV/' - базовое значение показателя качества к-го вида продукции; ак - относительный объем к-го вида продукции (коэффициент
вида продукции; IV/' - базовое значение показателя качества к-го вида продукции; ак - относительный объем к-го вида продукции (коэффициент  весомости):
весомости):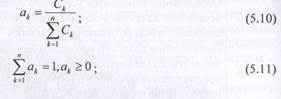



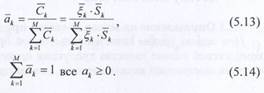

 геометрического индекса можно применять сре^° взвешенного арифметический индекс, когда усредненные ие ,1ИИ взвешенный относительных Показателей сравнительно мало отличак^одные значения Возможность такой замены оценивается по велич^ся ДРУГ от дРУга- ^
геометрического индекса можно применять сре^° взвешенного арифметический индекс, когда усредненные ие ,1ИИ взвешенный относительных Показателей сравнительно мало отличак^одные значения Возможность такой замены оценивается по велич^ся ДРУГ от дРУга- ^







 квантиль нормального распределения, отвечающий вероятности
квантиль нормального распределения, отвечающий вероятности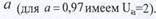


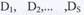 показатели О^, Ого,—
показатели О^, Ого,—


 /к
/к