
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегральные оценки качества переходных процессов в системе регулирования. Линейная интегральная оценка, квадратичная интегральная оценка, улучшенная интегральная квадратичная оценка.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Интегральные оценки – оценки качества переходного процесса, а именно быстроты затухания колебаний и величины отклонения регулируемой величины от установившегося значения. Применяются для процессов при отработке задающего воздействия. Удобны для сравнения близких по структуре систем, при этом лучшая система имеет меньшее значение ИО. В качестве подынтегральной функции при вычислении ИО при отработке задающих воздействий используется отклонение регулируемой величины от установившегося значения:
Линейная ИО:
На практике используют линейные ИО общего вида:
Недостаток: линейные ИО применимы только для монотонных процессов. Квадратичная ИО: Чем меньше I2, тем ближе начальная часть переходного процесса приближается к ступенчатой.
Улучшенная квадратичная ИО:
Чем меньше Iулуч, тем меньше отклонения переходного процесса от экспоненты с постоянной времени T. 24. Критерии устойчивости систем регулирования. Ценность критериев устойчивости. Алгебраический критерий устойчивости Гурвица: исходные данные; формулировка. Критерий устойчивости - Правило, позволяющее анализировать устойчивость без решения характеристического уравнения. Ценность критериев устойчивости не столько в устранении необходимости вычисления корней, сколько в том, что критерии позволяют просто установить причину неустойчивости, если таковая обнаружена. Найдя корни и установив, что система неустойчива, очень трудно определить, какой из параметров системы и в какую сторону можно изменять и сделать систему устойчивой. Использование критериев устойчивости позволяет проще решить эту систему. Критерий Гурвица Исходные данные – коэффициенты характеристического полинома замкнутой системы. Формулировка: Для того чтобы замкнутая система была устойчива необходимо и достаточно, чтобы все определители Гурвица имели знаки одинаковые со знаком первого коэффициента a0 характеристического уравнения замкнутой системы. Критическое значение коэффициента усиления - Это такой коэффициент, при котором система находится на границе устойчивости. При заданных параметрах системы коэффициент усиления принимается за неизвестный и определяется его критическое значение из (равенства) критерия Гурвица.
25. Критерии устойчивости систем регулирования. Ценность критериев устойчивости. Частотный критерий устойчивости Найквиста: исходные данные; формулировка в случаях устойчивой разомкнутой системы и системы находящейся на границе устойчивости. Ценность критериев устойчивости не столько в устранении необходимости вычисления корней, сколько в том, что критерии позволяют просто установить причину неустойчивости, если таковая обнаружена. Найдя корни и установив, что система неустойчива, очень трудно определить, какой из параметров системы и в какую сторону можно изменять и сделать систему устойчивой. Использование критериев устойчивости позволяет проще решить эту систему. Критерий Найквиста Исходные данные – проанализированная на устойчивость разомкнутая система. Если р.с. устойчива: Для того чтобы замкнутая система была устойчива необходимо и достаточно, чтобы АФЧХ разомкнутой системы при изменении частоты от 0 до +∞ не охватывает критическую точку (-1; j0). Если р.с. на границе устойчивости: Если количество нулевых корней S, то АФЧХ разомкнутой системы при изменении частоты от 0 до +∞ при частоте w=0 имеет разрыв и поворачивается от положительной вещественной оси по часовой стрелке на угол 90ºS. В случае одного нулевого корня для устойчивости замкнутой системы необходимо и достаточно, чтобы АФЧХ разомкнутой системы при изменении частоты от 0 до +∞, дополненная на участке разрыва дугой бесконечно большого радиуса, не охватывает критическую точку (-1; j0). В случае пары чисто мнимых корней АФЧХ разомкнутой системы на некоторой частоте дугой бесконечного радиуса перемещаются по часовой стрелке на угол в 180º.
рс устойчива, зс устойчива рс на границе, 1 нулевой рс на границе, пара мнимых корень, зс устойчива корней, зс устойчива
26. Критерии устойчивости систем регулирования. Ценность критериев устойчивости. Частотный критерий устойчивости Найквиста: исходные данные; формулировка в случае неустойчивой разомкнутой системы. Ценность критериев устойчивости не столько в устранении необходимости вычисления корней, сколько в том, что критерии позволяют просто установить причину неустойчивости, если таковая обнаружена. Найдя корни и установив, что система неустойчива, очень трудно определить, какой из параметров системы и в какую сторону можно изменять и сделать систему устойчивой. Использование критериев устойчивости позволяет проще решить эту систему. Критерий Найквиста
Если р.с. неустойчива: Для того чтобы замкнутая система была устойчива необходимо и достаточно, чтобы АФЧХ разомкнутой системы при изменении частоты от 0 до +∞ охватывала критическую точку (-1; j0) l/2 раз в положительном направлении. l – количество корней с положительной вещественной частью.
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-09; просмотров: 658; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.17.137 (0.008 с.) |







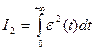


 где T – некоторая постоянная.
где T – некоторая постоянная.



 Исходные данные – проанализированная на устойчивость разомкнутая система.
Исходные данные – проанализированная на устойчивость разомкнутая система.


