
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определить понятие «качество процессов регулирования». По каким показателям (критериям) оценивается качество процесса регулирования.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Устойчивость системы – необходимое, но не достаточное условие работоспособности линейной системы. Качество процессов регулирования оценивается следующими критериями: а) переходные характеристики и их характер Переходными процессами называются переходные характеристики в замкнутой системе, регистрируемые при обработке стандартных единичных ступенчатых воздействий (задающих, возмущающих).Переходной процесс является одной из важнейших переходных характеристик динамических свойств системы регулирования. Переходной процесс позволяет судить о характере затухания переходных составляющих, которые возникают в системе при действии возмущения. б) ошибки систем регулирования в установившихся режимах Критерии оценки передающих свойств системы в установившемся режиме. Критерий оценки служит ее точность или значение ошибки регулирования в установившихся режимах. в) частотные критерии оценки качества процессов регулирования Частотные критерии – косвенные (оценка характера рабочего процесса производится по отображению этого процесса из области времени t в область частоты) К основным частотным критериям относятся: 1. Вид амплитудно-частотной или логарифмической характеристики разомкнутой системы. 2. Вид и характерные частоты вещественно-частотной характеристики замкнутой системы. 3. Характерные частоты, полоса пропускания которых и показатель колебательности М, АЧХ замкнутой системы. В некоторых случаях можно ограничиться только частотными критериями качества (полоса пропускания, М, частота среза, запасы устойчивости по амплитуде и по фазе не уточняя при этом вопрос в области времени). Среди возможных систем регулирования важное значение имеют переходные процессы, возникающие при быстром изменении Хзд или возмущения от одного значения до другого. Чем с большей скоростью и плавностью протекает такой процесс, тем меньше его продолжительность и величина рассогласования. Поэтому одной из оценок качестве регулировки явл. оценка качеств переходных процессов в замкнутой системе при обработке единичного случайного воздействия. Эти оценки качества называются прямыми. При этом имеетcя в виду, что чем лучше переходной процесс при обработке ступени воздействия тем лучше система будет отрабатывать произвольно задающее воздействие.
Переходные процессы при обработке задания делятся на следующие группы: а) Монотонные переходные процессы
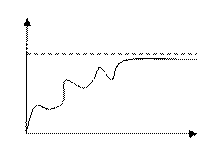
б) Колебательные с перерегулированием
в) Колебательные без перерегулирования
Особенность колебательных процессов заключается в наличии переходов через установленное значение. Если имеет место только перерегулирование то процесс называется малоколебательным. У монотонных переходных процессов не изменяется знак скорости т.е. производная =>0. К основным показателям качества переходных процессов относят: · Перерегулирование σ · Время регулирования tp · Время нарастания tн Перерегулированием оценивают разность междумах значением переходного процесса и его значением в установленном режиме, выражается в процентах: σ=(Ymax-Yуст)Yуст8*100% В большинстве случаях требуется, чтобы σ не превышало 10-30%. В некоторых случаях требуется чтобы перегрупир. отсутствовала и процесс был монотонным. Иногда допускается σ>50%. Время регулирования tp оценивают длительностью переходного процесса. В идеальной линейной системе переходной процесс длиться бесконечно, поэтому временем регулирования считают тот промежуток времен, по истечению которого отключение переходного процесс установлено значением не превышающее допускаемое значение. |Y(t)-Yуст|<Δ
2Δ= 5% от Yуст иногда 2Δ=2%, о такой выбор следует обосновывать. Время нарастания – длительность процесса от 0 до момента, когда Yt первый раз пересекает линию Yуст. Если заданы перерегулир и время регулирования, то переходной процесс не должен выходить за приделы определённой области, которую называют областью допустимого отклонения.
Число максимумов за время регулирования – число колебаний перех. процесса. Обычно на практике допускаются 1-2 колебательных процесса, иногда до 4-х. Всякая система регулирования имеет своей целью кроме воспроизведения задающих воздействий так же подавление или уменьшение влияния возмущений. Поэтому системы при отработке возмущения воздействий. Особенность переходных процессов при отработке возмущения заключается в том, что их установленное значение должно быть относительно малым в статической системе и =0 в астатической.
Переходной процесс пересекает ось абсцисс называется колебательным, не имеющий монотонности. Для определения времени служит то же значение зоны, которое используется при определении времени регулирования при отработке заданных воздействий. Эта зона для статической системы откладывается для оси абсцисс. Понятие перерегулирования для переходных процессов при отработке возмущений не имеет смысл. Поэтому эти переходные процессы оцениваются по мах значению отклонения регулировочного воздействия от оси абсцисс.
Точность систем регулирования в установившихся режимах. Точность систем регулирования относительно задающего воздействия. Переходные процессы в статических и астатических системах при отработке задающих воздействий. Реакция устойчивых систем на постоянные воздействия в установившимся режиме определяется: В установившемся режиме все члены с производными в диф. уравнении обращаются в 0 à если в перед. функциях положить оператор дифф. Р=0,то мы получаем перед. функции для установившимся режиме. Вспомним раздел перед. функций систем регулирования:
Пусть передаточная функция разомкнутой системы запишется как:
Эта перед. функция нормир.,т.е. свободные члены L(p) и N(p) =1.К-коэф. усил. разомкнутой системы Точность систем регулирования при отработке постоянных задающих воздействий Передаточная функция по регулируемой величине y(t), относительно задающего воздействия имеет следующий вид:
При пост. задающим воздействии Хзд., установившееся значение регулировочной величины записывается:
Фу,зд(0) передаточная функция относит. задающего воздействия для установившегося режима, т.е. когда переходные процессы завершены. Вид этой функции зависит от наличия или отсутствия интегрирующих звеньев в прямой цепи сист. Пример1: Система регулирования не содержит интегрирующих звеньев. Пусть регулятор – типовой регулятор прапорц.типа, т.е. ОУ - инерционное звено 1-го порядка,т.е.
В этом случае, передаточная функция разомкнутой системы не имеет нулевых полюсов, т.е.нет нулевых корней характеристического уравнения. Замкн. система:
Тогда установившееся значение Ууст.=Фу,зд(0)*Хзд =
Такие системы наз.статическими относ.зад. воздействия Пример2: Система регулирования содержит интегр. звенья. Пусть регулятор типовой интегральный: Wp(p)=1/Tup, регулятор астатический, а объект статический: Wpc(p)=Wp(p)W0(p)=Ko/Tup(T0p+1)=K0/Tu* Фу,зд(p)=K*N(p)/L(p)+KN(p)=K0/Tu L(0)=т.е. характеристический полином имеет нулевые корни Фу,зд(0)=1 т.е. Ууст=Фу,хзд(0)*Хзд0=1 Система астатическая относит задающ. воздействие в них У(t) точно соответствует заданию
Рассмотрим точность системы относительно ошибки регулирования. Пример: Wp(p)=Kp W0(p)=K0/T0p+1 N(0)=1 à L(0)=1 Eуст=Фе,хзд(0)*Хзд0=1/1+K
|
||||||
|
Последнее изменение этой страницы: 2016-12-09; просмотров: 440; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.197.120 (0.009 с.) |










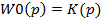 Такой регулятор наз. статическим.
Такой регулятор наз. статическим. , тоже статич.
, тоже статич.





 +Tup=K*N(p)/L(p)
+Tup=K*N(p)/L(p)




