
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Синтез систем регулирования методом модельного оптимума. Критерий оптимального модуля. Обоснование вида желаемой (базовой) передаточной функции замкнутой системы. Вывод условия оптимизации.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Синтез систем регулирования методом модельного оптимума и критерий оптимального модуля см. 36. Обоснование вида желаемой передаточной функции замкнутой системы. В качестве базовой передаточной функции замкнутой системы можно взять передаточную функцию колебательного звена:
Вопрос: Чем обосновать выбор передаточной функции колебательного звена в качестве базовой? Ответ:
Вывод условий оптимизации контура регулирования.
Из анализа полученного выражения, АЧХ замкнутой системы можно получить условия при выполнении которых график АЧХ будет близок хотя бы на низких частотах (включая нулевую) к единице. Предположим, что система – НЧ фильтр, то диапазон 0<ω<1. Чем меньше ω, тем меньше влияние ω4, следовательно, ей можно пренебречь. На нулевой частоте условие оптимизации контура регулирования:
Примечание: очевидно, что выполнение этого условия обеспечивает равенство единица амплитуды, только на нулевой частоте. Однако при низких частотах имеет место достаточно хорошее приближение амплитудной характеристики у единице. Синтез систем регулирования методом модельного оптимума. Математические модели объекта регулирования. Условия понижения порядка модели объекта. Выбор типа регулятора и параметров его настройки в случае, когда объект включает n инерционных звеньев первого порядка с соизмеримыми постоянными времени. Оптимальным можно назвать вид переходного процесса при отработке задания, когда переход из одного состояния в другое происходит сравнительно быстро, а существенного перерегулирования процесса не наблюдается. Именно такой формы переходной процесс пытаются добиться путём правильного выбора регулятора и параметров его настройки. Обычно работу контура регулирования оценивают по реакции на ступенчатое задающее воздействие даже в тех случаях, когда в дальнейшем нас будет интересовать и отработка возмущающего воздействия.
Взяв базовую передаточную функцию замкнутой системы. Логично вывести аналогичное выражение для АЧХ замкнутой системы.
Из анализа полученного выражения для АЧХ замкнутой системы можно получить условия, при выполнении которых график АЧХ будет близок хотябы на низких частотах, включая нулевую частоту, к единице, т.е. соответствовать выбранному нами критерию. Исходя из того, что система регулирования есть низкочастотный фильтр то 0≤w≤1, т.е. чем выше степень частоты в выражении, тем меньше её влияние на форму АЧХ, т.е. составляющей
Примечание: Очевидно, что выражение условия оптимизации обеспечивает равенство единицы амплитуды на нулевой частоте, однако при низких частотах имеет место достаточно хорошее приближение амплитудной характеристики к единице. Математическая модель объекта регулирования. В качестве модели объекта регулирования возьмём n-инерционных звеньев 1-го порядка с разными постоянными времени.
Поскольку в качестве базовой передаточной функции замкнутой системы мы взяли звено 2-го порядка, то модель объекта должна быть или должна иметь 1-й порядок.
В связи с этим возникает задача понижения порядка математической модели объекта от n-го порядка до 1-го. Эту модель 1-го порядка будем называть расчётной моделью, и использовать только для выбора типа регулятора и параметров его настройки, а при моделировании системы использовать реальную модель катого порядка.
S=KT
Для того, что бы понизить порядок модели от n-го до 1-го необходимо выполнение 2х условий: Наличие в прямой цепи системы интегрирующего звена Постоянная времени звена 1-го порядка должна равняться сумме постоянных времени полной модели Выбор типа регулятора и параметров его настройки в случае, когда объект включает n инерционных звеньев первого порядка с соизмеримыми постоянными времени.
Где Воспользовавшись условием оптимизации получим: Подставив полученную формулу для расчёта постоянной интегрирования в передаточную функцию замкнутой системы.
Полученная передаточная функция зависит только от 1-го параметра σ равного сумме постоянных времени. Определим коэффициент демпфирования этой передаточной функции.
Если сделать обратное преобразование Лапласа то получится:
Полученная передаточная функция замкнутой системы, построенная методом модального оптимума, называется стандартной передаточной функцией, а поскольку она зависит только от 1-го параметра то можно ввести относительное время tн=4,7σ – время нарастания tр=8,4σ – время регулирования Δy=4,3% - перерегулирование Это стандартные показатели качества регулирования. Синтез систем регулирования методом модельного оптимума. Математические модели объекта регулирования. Условия понижения порядка модели объекта. Выбор типа регулятора и параметров его настройки в случае, когда объект включает n инерционных звеньев первого порядка, одно из которых, имеет существенно большую постоянную времени. (начало смотри вопрос 38) Выбор типа регулятора и параметров его настройки в случае, когда объект включает n инерционных звеньев первого порядка, одно из которых, имеет существенно большую постоянную времени.
Чтобы уменьшить время регулирования необходимо каким-то образом компенсировать инерционность объекта связанную с наличием большой постоянной времени Т1 это можно сделать, используя более сложный регулятор ПИ-.
В качестве расчётной модели выберем следующую модель:
Запишем передаточную функцию разомкнутой системы
Подставив полученные выражения
tн=4,7σ – время нарастания tр=8,4σ – время регулирования Δy=4,3% - перерегулирование Синтез систем регулирования методом модельного оптимума. Математические модели объекта регулирования. Условия понижения порядка модели объекта. Выбор типа регулятора и параметров его настройки в случае, когда объект включает n инерционных звеньев первого порядка два из которых имеют существенно большие постоянные времени. (начало смотри вопрос 38) Выбор типа регулятора и параметров его настройки в случае, когда объект включает n инерционных звеньев первого порядка два из которых имеют существенно большие постоянные времени.
Пусть
Исходя из условия компенсации большой постоянной времени, есть смысл выбрать
Анализ выражения показывает, что оно аналогично предыдущему пункту, т.е. плучим стандартную передаточную функцию (смотри 39 вопрос). Понижение прядка передаточной функции замкнутой системы построенной методом модального оптимума до 1-го порядка т.е.
Если ограничится только линейной частью то
|
||||
|
Последнее изменение этой страницы: 2016-12-09; просмотров: 710; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.255.198 (0.007 с.) |







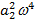 можно пренебречь.
можно пренебречь.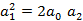 - условие оптимизации контура регулирования.
- условие оптимизации контура регулирования.










 ,
,  ,
, 







 .
.


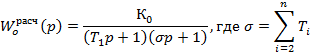


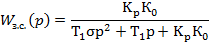

 в передаточную функцию замкнутой системы, получим:
в передаточную функцию замкнутой системы, получим:

 для того что бы скомпенсировать 2 инерционности используется ПИД - регулятор
для того что бы скомпенсировать 2 инерционности используется ПИД - регулятор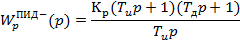

 .
.





