
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Что является объектом изучения теории автоматического управления (тау). Перечислить основные задачи линейной тау.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Что является объектом изучения теории автоматического управления (ТАУ). Перечислить основные задачи линейной ТАУ. Объект (и предмет): Системы автоматического управления и процессы, протекающие в них. Задачи: Ø Изучение динамических свойств различных типовых звеньев автоматических систем. Ø Формирование функциональных и структурных схем автоматических систем из типовых звеньев. Ø Определение качества систем управления в установившихся режимах (точность систем). Ø Определение качества систем в переходных режимах (качество переходных процессов). Ø Исследование устойчивости автоматических систем управления. Ø Изучение различных корректирующих устройств, которые вводятся в систему управления для повышения точности и улучшения качества переходных процессов систем. Ø Создание различных методов синтеза корректирующих устройств и методов оптимизации систем по различным показателям качества. Сформулировать принцип действия автоматического устройства управления. Схема объекта управления (ОУ). Состояние ОУ. Что понимают под управлением объектом. Принципиальная схема автоматического управления объектом. Задача автоматического управления. Принцип действия: Обнаружить отклонения параметров, характеризующих работу объекта управления, от заданных для него законов изменения и воздействия на объект таким образом, чтобы устранить заданное отклонение от данного режима. Схема ОУ:
ОУ – объект управления X(t) – управляемая (регулируемая, выходная) величина F(t) – возмущающее воздействие Xp(t) – управляющее (регулирующее) воздействие Состояние ОУ: Величина X(t) характеризует состояние объекта управления. Состояние ОУ может характеризоваться не одной, а несколькими величинами. Примеры: электродвигатель – частота вращения вала и ток в якоре; автомобиль – скорость и направление; холодильник – tº воздуха; душ – tº воды; производственное предприятие – прибыль, объём выпуска, объём продаж и т.д. Управление объектом: Управлять объектом означает сформулировать на входе объекта управляющее воздействия Xp(t), которое целенаправленно изменит его состояние. Принципиальная схема автоматического управления объектом:
АУУ – автоматическое устройство управления ИУ – исполнительное устройство, предназначено для преобразования Xp(t) в Xp*(t) ОУ – объект управления Xзд(t) – задающее воздействие, характеризующее требуемое состояние ОУ Xp(t) – управляющее (регулирующее) воздействие Xp*(t) – управляющее (регулирующее) воздействие той физической природы, которая определяется природой ОУ F(t) – возмущающее воздействие X(t) – управляемая (регулируемая, выходная) величина Задача автоматического управления: Как можно точнее воспроизводить на выходе объекта заданный закон изменения задающего воздействия и как можно полнее подавлять влияние возмущающих воздействий F(t).
Определить понятие «принципы управления». Сущность, достоинства, недостатки и принципиальные схемы следующих принципов управления: разомкнутое управление; управление по возмущению; управление с обратной связью. Автоматические системы регулирования (АСР). Принцип управления – способ увязки алгоритма управления системы с заданным и фактическим её функционированием. Разомкнутое управление:
   
ЗД – специальное устройство, которое формирует задающее воздействие АУУ – автоматическое устройство управления ИУ – исполнительное устройство, предназначено для преобразования Xp(t) в Xp*(t) ОУ – объект управления Xзд(t) – задающее воздействие, характеризующее требуемое состояние ОУ Xp(t) – управляющее (регулирующее) воздействие Xp*(t) – управляющее (регулирующее) воздействие той физической природы, которая определяется природой ОУ F(t) – возмущающее воздействие X(t) – управляемая (регулируемая, выходная) величина Сущность – управляющее воздействие Xp(t) вырабатывается только на основе заданного заранее алгоритма функционирования АУУ. Недостаток – алгоритм функционирования не связан с такими факторами как F(t) и фактическим состоянием управляющей величины Х(t). Управление по возмущению:
Сущность – измеряют наиболее существенное возмущение и передают эту информацию АУУ, которое имеет возможность компенсировать отклонение управляемой величины X(t), вызванное этим возмущением. Недостатки – 1) АУУ не имеет информации о фактическом состоянии Х(t), т.е. система не знает насколько Х(t) соответствует заданному значению Хзд(t). 2) Далеко не всегда имеются датчики для измерения наиболее существенных возмущений. Управление с обратной связью:
Сущность – измеряют фактическое состояние управляемой величины X(t) и передают эту информацию АУУ. Чаще всего управляющее воздействие Xp(t) формируется по отклонению фактического состояния от заданного значения:
Автоматические системы регулирования: Управление с использованием отклонения E(t) фактического состояния от заданного значения называется регулированием, а АУУ называются автоматическим регулятором. АСУ, состоящая из СЭ (сравнивающий элемент), АР, ИУ и ОЭ в прямой цепи системы, охваченной главной обратной связью (всегда отрицательна), называется замкнутой АСР. Передаточные функции АСР. Структурная схема одноконтурной АСР с единичной обратной связью. Передаточная функция разомкнутой системы. Передаточные функции замкнутой системы регулирования относительно задающего воздействия, внутреннего и внешнего возмущений. Характеристические полиномы разомкнутой и замкнутой систем регулирования. Структурная схема одноконтурной АСР с единичной обратной связью:
Wp(p) – передаточная функция регулятора Wо(p) – передаточная функция объекта F1(t) – возмущающее воздействие, приложенное ко входу объекта (внутреннее) F2(t) – возмущающее воздействие, приложенное к выходу объекта (внешнее) Передаточная функция разомкнутой системы: Если в структурной схеме одноконтурной системе регулирования с единичной ОС разомкнуть ОС у сумматора, то получится структурная схема разомкнутой АСР. Разомкнутая АСР состоит из последовательно включённых звеньев различной сложности.
Используется для анализа устойчивости замкнутой системы с использованием критерия Найквиста и для синтеза систем регулирования, т.е. при определнии параметров настройки регулятора. Передаточные функции замкнутой системы регулирования: Ø Относительно задающего воздействия
Ø Относительно внутреннего возмущающего воздействия
Ø Относительно внешнего возмущающего воздействия
Характеристические полиномы разомкнутой и замкнутой систем регулирования:
где L(p) – характеристический полином разомкнутой системы.
где A(p) – характеристический полином разомкнутой системы. Корни полинома A(p) – полюса ПФ замкнутой системы, а корни полинома В(p) – нули. 11. Частотные характеристики элементов (систем). Физический смысл частотных характеристик. Способы определения частотных характеристик. Виды частотных характеристик. Графическое представление частотных характеристик. Физический смысл: Если на вход системы подать гармонический сигнал с постоянной амплитудой и частотой
то после завершения переходных процессов в системе на выходе устанавливаются незатухающие гармонические колебания
Способы определения: АЧХ, ФЧХ – экспериментально. Для этого необходимо иметь генератор гармонических колебаний, который подключается к входу объекта, и измерительную аппаратуру для измерения амплитуды и фазового сдвига колебаний на выходе объекта. Все частотные – аналитически. Для получения частотной ПФ надо сделать в W(p) подстановку p=jω.
где U(ω) – ВЧХ, V(ω) – МЧХ, A(ω) – АЧХ, φ(ω) – ФЧХ. Виды:
где U(ω) – ВЧХ, V(ω) – МЧХ, A(ω) – АЧХ, φ(ω) – ФЧХ.
где ln(A(ω)) (на практике используется 20*lg(A(ω))) – ЛАХ, φ(ω) – ЛФХ.
Графическое представление: Рассмотрим комплексную плоскость, на которой каждой частоте частотной передаточной функции соответствует вектор.
Кривую, которая описывает конец вектора при изменении частоты от -∞ до +∞, называют годографом АФЧХ. Годограф строится в диапазоне частот от 0 до +∞, т.к. математически обосновано, что часть годографа для частот от -∞ до 0 симметрична. Типовые элементы (звенья) линейных АСР. Уравнение, передаточная функция и переходная характеристика следующих типовых элементов: пропорциональное (усилительное); инерционное первого порядка; реальное дифференцирующее. Типовыми звеньями систем регулирования называют элементы различной физической природы и конструкции, которые описаны уравнениями определенного типа.
Инерционное звено 1 порядка:
Реального дифференцирующее звено:
Типовые элементы (звенья) линейных АСР. Уравнение, передаточная функция и переходная характеристика следующих типовых элементов: интегрирующее; инерционное второго порядка; интегро-дифференцирующее звено. Типовыми звеньями систем регулирования называют элементы различной физической природы и конструкции, которые описаны уравнениями определенного типа. Интегрирующее звено:
Инерционное звено 2 порядка:
Интегро-дифференцирующее звено:
Колебательное звено:
Типовые модели промышленных объектов регулирования в виде передаточных функций. Уравнение, передаточная функция и переходная характеристика следующих типовых законов регулирования: пропорциональный (П-); интегральный (И-), пропорционально-интегральный ПИ-). Типовые модели:
П-регулятор:
где Kp– коэффициент пропорциональности, ε(t) – отклонение регулируемой величины от установившегося значения.
И-регулятор:
где ТИ – постоянная времени интегрирования
ПИ-регулятор:
где ТИ – постоянная времени интегрирования, Kр– коэффициент пропорциональности
Точность систем регулирования в установившихся режимах. Точность систем регулирования относительно задающего воздействия. Переходные процессы в статических и астатических системах при отработке задающих воздействий. Реакция устойчивых систем на постоянные воздействия в установившимся режиме определяется: В установившемся режиме все члены с производными в диф. уравнении обращаются в 0 à если в перед. функциях положить оператор дифф. Р=0,то мы получаем перед. функции для установившимся режиме. Вспомним раздел перед. функций систем регулирования:
Пусть передаточная функция разомкнутой системы запишется как:
Эта перед. функция нормир.,т.е. свободные члены L(p) и N(p) =1.К-коэф. усил. разомкнутой системы Точность систем регулирования при отработке постоянных задающих воздействий Передаточная функция по регулируемой величине y(t), относительно задающего воздействия имеет следующий вид:
При пост. задающим воздействии Хзд., установившееся значение регулировочной величины записывается:
Фу,зд(0) передаточная функция относит. задающего воздействия для установившегося режима, т.е. когда переходные процессы завершены. Вид этой функции зависит от наличия или отсутствия интегрирующих звеньев в прямой цепи сист. Пример1: Система регулирования не содержит интегрирующих звеньев. Пусть регулятор – типовой регулятор прапорц.типа, т.е. ОУ - инерционное звено 1-го порядка,т.е.
В этом случае, передаточная функция разомкнутой системы не имеет нулевых полюсов, т.е.нет нулевых корней характеристического уравнения. Замкн. система:
Тогда установившееся значение Ууст.=Фу,зд(0)*Хзд =
Такие системы наз.статическими относ.зад. воздействия Пример2: Система регулирования содержит интегр. звенья. Пусть регулятор типовой интегральный: Wp(p)=1/Tup, регулятор астатический, а объект статический: Wpc(p)=Wp(p)W0(p)=Ko/Tup(T0p+1)=K0/Tu* Фу,зд(p)=K*N(p)/L(p)+KN(p)=K0/Tu L(0)=т.е. характеристический полином имеет нулевые корни Фу,зд(0)=1 т.е. Ууст=Фу,хзд(0)*Хзд0=1 Система астатическая относит задающ. воздействие в них У(t) точно соответствует заданию
Рассмотрим точность системы относительно ошибки регулирования. Пример: Wp(p)=Kp W0(p)=K0/T0p+1 N(0)=1 à L(0)=1 Eуст=Фе,хзд(0)*Хзд0=1/1+K
Частные задачи, решаемые при создании эффективных (качественных) систем регулирования. Структурные схемы систем регулирования с дополнительными местными обратными связями: каскадные двухконтурные и трехконтурные системы; системы с дифференцированием промежуточной регулируемой величины. Проблема создания линейных непрерывных систем регулирования с хорошими динамичискими свойствами является многосторонней и сложной задачей. В ней можно выделить частные задачи: · обеспечение устойчивости (стабилизации) · повышение запаса устойчивости (демпфирование) · повышение точности в установившихся режимах (уменьшение или устранение статической ошибки при отработки задающего воздействия и ошибки при отработке возмущения) · улучшение переходных процессов (увеличение быстродействия, максимальное уменьшение динамических ошибок воспроизведения задающего воздействия и ошибки от возмущающих воздействий) В некоторых случаях две или несколько задач могут решаться одновременно. Простой и действенный способ обеспечения устойчивости и высокого качества регулирования это выбор основных элементов системы или изменение в нужном направлении их динамических свойств с помощью местных ОС. Местные ОС позволяют существенно изменять свойства элементов. С их помощью можно обеспечить устойчивость неустойчивого элемента, уменьшить инерционность, обеспечить интегрирующие и дифференцирующие свойства. Другой путь – создание дополнительных воздействий на регулятор или объект регулирования. Если эти воздействия осуществляются извне системы, то получаем комбинированную систему управления.
Рисунок 1 – Двухконтурная каскадная система
Рисунок 2 – Трёхконтурная каскадная система
Рисунок 3 – Схема дифференцирования промежуточной регулироваемой величины Wky – корректирующее устройство. Повышение статической точности. Ошибка в установившихся режимах с.р слагается из составляющих: 1. несовершенство регулятора 2. ошибки воспроизведения задающего воздействия 3. ошибки, создаваемые возмущением Для уменьшения 1: использование более совершенных элементов и сопровождается увеличением сложности и стоимости регулятора Для уменьшения 2-3: использование следующие пути: 1. увеличение коэффициента усиления разомкнутой системы. Является универсальным и эффективным способом уменьшения ошибки в установившихся режимах. Достигается введением в систему усилителей. Иногда достаточно увеличить коэффициент отдельных элементов. Увеличение коэффициента усиления разомкнутой системы ведет УК уменьшению запаса устойчивости. Чтобы такое не произошло, коэффициент усиления разомкнутой системы не должен превышать известного значения (критическое). На практике приближение к критическому значению невозможно из-за резкого ухудшения показателей качества переходных процессов. В этом противоречие между требованием к точности и требованием устойчивости. Оно устраняется, если одновременно с увеличением коэффициента усиления, обеспечивающего необходимую точность, какими-либо другими средствами обеспечить запас устойчивости. К таким средствам относится корректирующее устройство. 2. обеспечение устойчивости и запаса устойчивости. Распространенный способ – введение в систему дополнительных звеньев. Эти звенья могут включаться несколькими способами: 2.1. последовательно, в прямую цепь системы 2.2. параллельно отдельным участкам системы 2.3. охват системы ОС В качестве дополнительных звеньев используют: · интегрирующие · инерционные (апериодические) · дифференциальные · интегрально-дифференциальные Эти способы улучшения динамических свойств отличаются различным влиянием на частотные характеристики различных систем (АЧХ, АХ и ФХ) Демпфирование с подавлением высоких частот. Устойчивость замкнутой системы и запас устойчивости обеспечиваются в этом случае посредством предания раз. системе способности подавлять гармонические колебания, частота которых превышает некоторое значение. Если разомкнутая система состоит из безинерционных (усилительных), апериодических (инерционных), колебательных и форсирующих звеньев, то для подавления высоких частот достаточно включить апериодическое звено с большой постоянной времени. Демпфирование с повышением высоких частот. Устойчивость и нужный запас устойчивости обеспечиваются посредством увеличения способности раз. системы пропускать гармонические колебания, частота которых больше некоторого значения. Достигается путем включения в прямую цепь форсирующего звена: Wф (t)=Tp+1 Преимущество этого способа в том, что увеличивается быстродействие системы за счет увеличения полосы пропускания для полезного задающего сигнала. Недостаток – повышается пропускаемость системой уровня высокочастотных помех. Синтез систем регулирования методом модельного оптимума. Математические модели объекта регулирования. Условия понижения порядка модели объекта. Выбор типа регулятора и параметров его настройки в случае, когда объект включает n инерционных звеньев первого порядка с соизмеримыми постоянными времени. Оптимальным можно назвать вид переходного процесса при отработке задания, когда переход из одного состояния в другое происходит сравнительно быстро, а существенного перерегулирования процесса не наблюдается. Именно такой формы переходной процесс пытаются добиться путём правильного выбора регулятора и параметров его настройки. Обычно работу контура регулирования оценивают по реакции на ступенчатое задающее воздействие даже в тех случаях, когда в дальнейшем нас будет интересовать и отработка возмущающего воздействия.
Взяв базовую передаточную функцию замкнутой системы. Логично вывести аналогичное выражение для АЧХ замкнутой системы.
Из анализа полученного выражения для АЧХ замкнутой системы можно получить условия, при выполнении которых график АЧХ будет близок хотябы на низких частотах, включая нулевую частоту, к единице, т.е. соответствовать выбранному нами критерию. Исходя из того, что система регулирования есть низкочастотный фильтр то 0≤w≤1, т.е. чем выше степень частоты в выражении, тем меньше её влияние на форму АЧХ, т.е. составляющей
Примечание: Очевидно, что выражение условия оптимизации обеспечивает равенство единицы амплитуды на нулевой частоте, однако при низких частотах имеет место достаточно хорошее приближение амплитудной характеристики к единице. Математическая модель объекта регулирования. В качестве модели объекта регулирования возьмём n-инерционных звеньев 1-го порядка с разными постоянными времени.
Поскольку в качестве базовой передаточной функции замкнутой системы мы взяли звено 2-го порядка, то модель объекта должна быть или должна иметь 1-й порядок.
В связи с этим возникает задача понижения порядка математической модели объекта от n-го порядка до 1-го. Эту модель 1-го порядка будем называть расчётной моделью, и использовать только для выбора типа регулятора и параметров его настройки, а при моделировании системы использовать реальную модель катого порядка.
S=KT
Для того, что бы понизить порядок модели от n-го до 1-го необходимо выполнение 2х условий: Наличие в прямой цепи системы интегрирующего звена Постоянная времени звена 1-го порядка должна равняться сумме постоянных времени полной модели Выбор типа регулятора и параметров его настройки в случае, когда объект включает n инерционных звеньев первого порядка с соизмеримыми постоянными времени.
Где Воспользовавшись условием оптимизации получим: Подставив полученную формулу для расчёта постоянной интегрирования в передаточную функцию замкнутой системы.
Полученная передаточная функция зависит только от 1-го параметра σ равного сумме постоянных времени. Определим коэффициент демпфирования этой передаточной функции.
Если сделать обратное преобразование Лапласа то получится:
Полученная передаточная функция замкнутой системы, построенная методом модального оптимума, называется стандартной передаточной функцией, а поскольку она зависит только от 1-го параметра то можно ввести относительное время tн=4,7σ – время нарастания tр=8,4σ – время регулирования Δy=4,3% - перерегулирование Это стандартные показатели качества регулирования. Синтез систем регулирования методом модельного оптимума. Математические модели объекта регулирования. Условия понижения порядка модели объекта. Выбор типа регулятора и параметров его настройки в случае, когда объект включает n инерционных звеньев первого порядка, одно из которых, имеет существенно большую постоянную времени. (начало смотри вопрос 38) Выбор типа регулятора и параметров его настройки в случае, когда объект включает n инерционных звеньев первого порядка, одно из которых, имеет существенно большую постоянную времени.
Чтобы уменьшить время регулирования необходимо каким-то образом компенсировать инерционность объекта связанную с наличием большой постоянной времени Т1 это можно сделать, используя более сложный регулятор ПИ-.
В качестве расчётной модели выберем следующую модель:
Запишем передаточную функцию разомкнутой системы
Подставив полученные выражения
tн=4,7σ – время нарастания tр=8,4σ – время регулирования Δy=4,3% - перерегулирование Синтез систем регулирования методом модельного оптимума. Математические модели объекта регулирования. Условия понижения порядка модели объекта. Выбор типа регулятора и параметров его настройки в случае, когда объект включает n инерционных звеньев первого порядка два из которых имеют существенно большие постоянные времени. (начало смотри вопрос 38) Выбор типа регулятора и параметров его настройки в случае, когда объект включает n инерционных звеньев первого порядка два из которых имеют существенно большие постоянные времени.
Пусть
Исходя из условия компенсации большой постоянной времени, есть смысл выбрать
Анализ выражения показывает, что оно аналогично предыдущему пункту, т.е. плучим стандартную передаточную функцию (смотри 39 вопрос). Понижение прядка передаточной функции замкнутой системы построенной методом модального оптимума до 1-го порядка т.е.
Если ограничится только линейной частью то Синтез систем регулирования методом симметричного оптимума. Выбор типа регулятора и параметров его настройки, когда объект включает одно интегрирующее звено и n инерционных звеньев с соизмеримыми постоянными времени.
В этом случае целесообразно использовать ПИД регулятор:
y(t)
Компенсировать большую инерционность
Большое перерегулирование обусловлено тем, что числитель обладает дифференцирующими свойствами (упреждением). Синтез систем регулирования методом симметричного оптимума. Выбор типа регулятора и параметров его настройки, когда объект включает одно интегрирующее звено и n инерционных звеньев одно из которых имеет существенно большую постоянную времени. (начало смотри вопрос 45) Выбор типа регулятора и параметров его настройки, когда объект включает одно интегрирующее звено и n инерционных звеньев одно из которых имеет существенно большую постоянную времени.
Компенсировать большую инерционность T1 можно за счёт соответственно выбора постоянной дифференцирования
Отметим, что полученная передаточная функция разомкнутой системы имеет тот же вид, что и в предыдущем случае, если применить условие оптимума, то получим те же Кр Ти. В итоге получим стандартный вид передаточной функции. (смотри вопрос 45) Отметим, что перерегулирование >43% в реальных системах, за редким исключением недопустимо.
Что является объектом изучения теории автоматического управления (ТАУ). Перечислить основные задачи линейной ТАУ. Объект (и предмет): Системы автоматического управления и процессы, протекающие в них. Задачи: Ø Изучение динамических свойств различных типовых звеньев автоматических систем. Ø Формирование функциональных и структурных схем автоматичес
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-09; просмотров: 583; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.113.24 (0.01 с.) |




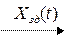
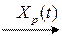
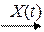















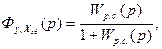













 Пропорциональное звено:
Пропорциональное звено:












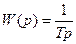










 – инерционное звено 1 порядка с запаздыванием
– инерционное звено 1 порядка с запаздыванием





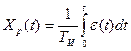









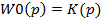 Такой регулятор наз. статическим.
Такой регулятор наз. статическим. , тоже статич.
, тоже статич.





 +Tup=K*N(p)/L(p)
+Tup=K*N(p)/L(p)

 Дополнительное воздействие создаётся и внутри замкнутого контура регулирования (каскадные системы регулирования и дифференцирование промежуточной регулируемой величины)
Дополнительное воздействие создаётся и внутри замкнутого контура регулирования (каскадные системы регулирования и дифференцирование промежуточной регулируемой величины)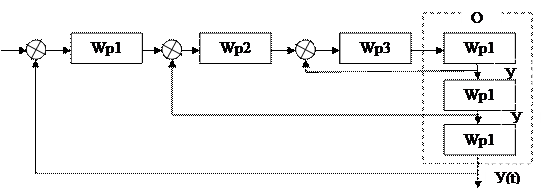
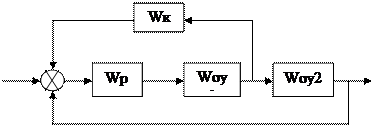



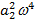 можно пренебречь.
можно пренебречь.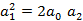 - условие оптимизации контура регулирования.
- условие оптимизации контура регулирования.










 ,
,  ,
, 







 .
.


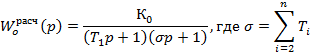


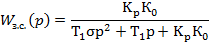

 в передаточную функцию замкнутой системы, получим:
в передаточную функцию замкнутой системы, получим:

 для того что бы скомпенсировать 2 инерционности используется ПИД - регулятор
для того что бы скомпенсировать 2 инерционности используется ПИД - регулятор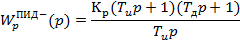

 .
.


 ;
; 
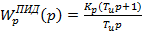 ;
;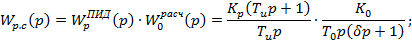

 и подставим в
и подставим в 
 ;
;
 2%
2% 




 =>
=> 
 можно
можно 



 .
.



