Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Назначение структурных схем. Виды структурных схем. Элементы алгоритмических структурных схем.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Назначение: Наглядное представление сложных автоматических систем как совокупности элементов и связей между ними. Виды: Ø Функциональные Элементы – функциональные устройства (задающие, сравнивающие, устройства управления, исполнения, датчики). Ø Конструктивные Элементы – конструктивные блоки, объединяющие ряд элементов (например, задающее устройство, сравнивающее устройство, устройство автоматического управления и часть исполнительного устройства) в конструктивное целое (цифровой регулятор). Конструктивные схемы используются при монтаже АСР. Ø Алгоритмические Элементы – звенья (соответствующие выполняемым в них математических преобразованиям), сумматоры, узлы. Используются в ТАУ для определения ПФ замкнутой систем относительно задающих и возмущающих воздействий, а также при решении задач синтеза систем. Представляют собой графическое изображение матмоделей АСР в виде соединения звеньев. Звенья выбирают так, чтобы воздействия в них передавались только в одном направлении. 8. Правила преобразования структурных схем: последовательное соединение звеньев; параллельное соединение; охват звена обратной связью. Последовательное соединение: Последовательное соединение передаточных функций звеньев можно заменить на одно эквивалентное звено с передаточной функцией, равной произведению передаточных функций звеньев.
Если знак ОС «+», то в формуле будет «–». 9. Правила преобразования структурных схем: перенос сумматора; перенос узла (точки) разветвления. Правило Мейсона (Мэзона) преобразования структурных схем. Перенос сумматора: Ø По направлению сигнала
Ø Против направления сигнала
Перенос узла разветвления: Ø Через звено по направлению сигнала
Ø Через звено по направлению сигнала
Ø Через сумматор по направлению сигнала
Ø Через сумматор против направления сигнала
Правило Мейсона:
где n – количество прямых путей от заданного входа к заданному выходу, Hi – передаточная функция i-того прямого пути, Фi – Ф за исключением передаточных функций контуров, которые пересекаются с i-тым прямым путём,
где n1 – количество замкнутых контуров в системе, H1i – передаточная функция i-того разомкнутого контура с учетом его знака, n2… – количество пар (троек, четвёрок и т.д.) пересекающихся контуров, H2…i – передаточная функция пары (тройки, четвёрки и т.д.) разомкнутых контуров с учетом знака. Передаточные функции АСР. Структурная схема одноконтурной АСР с единичной обратной связью. Передаточная функция разомкнутой системы. Передаточные функции замкнутой системы регулирования относительно задающего воздействия, внутреннего и внешнего возмущений. Характеристические полиномы разомкнутой и замкнутой систем регулирования. Структурная схема одноконтурной АСР с единичной обратной связью:
Wp(p) – передаточная функция регулятора Wо(p) – передаточная функция объекта F1(t) – возмущающее воздействие, приложенное ко входу объекта (внутреннее) F2(t) – возмущающее воздействие, приложенное к выходу объекта (внешнее) Передаточная функция разомкнутой системы: Если в структурной схеме одноконтурной системе регулирования с единичной ОС разомкнуть ОС у сумматора, то получится структурная схема разомкнутой АСР. Разомкнутая АСР состоит из последовательно включённых звеньев различной сложности.
Используется для анализа устойчивости замкнутой системы с использованием критерия Найквиста и для синтеза систем регулирования, т.е. при определнии параметров настройки регулятора. Передаточные функции замкнутой системы регулирования: Ø Относительно задающего воздействия
Ø Относительно внутреннего возмущающего воздействия
Ø Относительно внешнего возмущающего воздействия
Характеристические полиномы разомкнутой и замкнутой систем регулирования:
где L(p) – характеристический полином разомкнутой системы.
где A(p) – характеристический полином разомкнутой системы. Корни полинома A(p) – полюса ПФ замкнутой системы, а корни полинома В(p) – нули. 11. Частотные характеристики элементов (систем). Физический смысл частотных характеристик. Способы определения частотных характеристик. Виды частотных характеристик. Графическое представление частотных характеристик. Физический смысл: Если на вход системы подать гармонический сигнал с постоянной амплитудой и частотой
то после завершения переходных процессов в системе на выходе устанавливаются незатухающие гармонические колебания
Способы определения: АЧХ, ФЧХ – экспериментально. Для этого необходимо иметь генератор гармонических колебаний, который подключается к входу объекта, и измерительную аппаратуру для измерения амплитуды и фазового сдвига колебаний на выходе объекта. Все частотные – аналитически. Для получения частотной ПФ надо сделать в W(p) подстановку p=jω.
где U(ω) – ВЧХ, V(ω) – МЧХ, A(ω) – АЧХ, φ(ω) – ФЧХ. Виды:
где U(ω) – ВЧХ, V(ω) – МЧХ, A(ω) – АЧХ, φ(ω) – ФЧХ.
где ln(A(ω)) (на практике используется 20*lg(A(ω))) – ЛАХ, φ(ω) – ЛФХ.
Графическое представление: Рассмотрим комплексную плоскость, на которой каждой частоте частотной передаточной функции соответствует вектор.
Кривую, которая описывает конец вектора при изменении частоты от -∞ до +∞, называют годографом АФЧХ. Годограф строится в диапазоне частот от 0 до +∞, т.к. математически обосновано, что часть годографа для частот от -∞ до 0 симметрична.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-09; просмотров: 934; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.242.56 (0.009 с.) |





 Параллельное соединение: Параллельное соединение передаточных функций звеньев можно заменить на одно эквивалентное звено с передаточной функцией, равной сумме передаточных функций звеньев.
Параллельное соединение: Параллельное соединение передаточных функций звеньев можно заменить на одно эквивалентное звено с передаточной функцией, равной сумме передаточных функций звеньев.




 Охват звена обратной связью:
Охват звена обратной связью: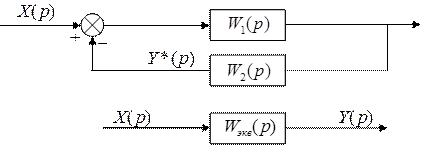


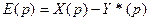

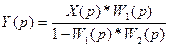















 ,
, ,
,