
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Результати дослідження мотивації навчанняСодержание книги
Поиск на нашем сайте
студентів агрономічного та юридичного факультетів (1 курс) аграрного університету*
*У таблиці розподіл студентів юридичного та агрономічного факультетів за мотивами навчання подано у відсотках. Через те, що респонденти могли вибрати більше одного мотиву навчання, сума стовпчиків не дорівнює 100%. Оскільки обидві змінні вимірюються у шкалах порядка (рангова шкала), то як міру зв’язку використаємо коефіцієнт рангової кореляції Спірмена. Він вираховується за формулою:
де
Зупинимося на особливостях заповнення таблиці 8.11. У графі таблиці «юридичний факультет» зустрічаються два однакових числа (50,9). У таких випадках обом числам присвоюється ранг, рівний середньому арифметичному з рангів, які б вони зайняли (3 і 4):
Практика показує, що ця операція викликає певні труднощі у дослідників, а тому доцільно доповнити цей матеріал таким уявним прикладом: експерт при ранжуванні певних об’єктів отримав розподіл: 1; 1; 1; 2; 3; 4; 5; 6. Як бачимо, на перше місце поставлено 3 об’єкти. Значить ці об’єкти зайняли 1, 2 і 3 місця в ранжованому ряді. Тому знаходимо суму 1+2+3=6, ділимо її на 3 і присвоюємо зазначеним об’єктам один ранг «2».Тоді ряд буде мати такий вигляд: 2; 2; 2; 4; 5; 6; 7; 8. Щоб перевірити правильність дій, варто знайти суму усіх рангів. Якщо ранжують 8 об’єктів, то їх сума у будь-якому випадку (незалежно від того, були «зв’язані» ранги чи ні) повинна дорів-нювати 36. Звісно, якщо ранжованих об’єктів 9, то ця сума буде дорівнювати 45; 10 – 55; 11 – 66 і т.д. Підставимо величини, вирахувані в таблиці 8.11 у формулу (10):
Таку величину коефіцієнта кореляції можна інтерпретувати як високу ступінь зв’язку між мотивами навчання студентів двох різних факультетів – агрономічного та юридичного. Але, разом з тим, така величина коефіцієнта кореляції не повинна ввести в оману дослідника: мотиви навчання студентів обох факультетів чітко розподіляються на дві групи. За першими чотирма мотивами єдності думок респондентів не спостерігається. А для іншої групи мотивів (5; 6; 7; 8) ранги повністю співпадають. Отже, крім визначення величини коефіцієнта рангової кореляції, обробку даних експерименту слід доповнити якісним аналізом таблиці 8.11. Розглянувши приклади визначення коефіцієнта кореляції, зупини-мося на аспектах статистичної значущості цього показника. Іншими словами, треба дати відповідь на питання: «Чи не обумовлена за-лежність, яку він фіксує, випадковими відхиленнями?» (перевіряється гіпотеза того, що отримані дані «суттєво» відрізняються від 0). Якщо гіпотезу Розглянемо процедуру перевірки статистичної значущості коефі-цієнта кореляції Пірсона. 1 випадок. Коли число респондентів
За таблицями критичних значень для
де
Вибираємо рівень значущості (переважно, не більше 0,05) і порівнюємо розраховане і критичне значення критерію 2 випадок. Коли число респондентів
За таблицями критичних значень знаходимо величину Zкр для відповідного λ. Аналіз отриманих даних виконуємо аналогічно 1 випадку. Наведемо приклад визначення статистичної значущості коефіцієнта кореляції Пірсона для умов: Тоді Для рівня значущості Перевірка статистичної значущості коефіцієнта кореляції Спірмена. Значущість коефіцієнта кореляції Спірмена визначається залежними від Якщо Наприклад, використовуючи дані таблиці, де Якщо
де
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-09; просмотров: 497; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.007 с.) |

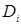


 , (10)
, (10)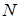 – число пар рангів, що зіставляються.
– число пар рангів, що зіставляються. .
.
 (
( ) буде відхилено, стверджують, що величина коефіцієнта кореляції статистично значуща (ця величина не обумовлена випадковістю) при рівні значущості
) буде відхилено, стверджують, що величина коефіцієнта кореляції статистично значуща (ця величина не обумовлена випадковістю) при рівні значущості  .
.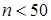 , застосовується кри-терій розподілу Стьюдента
, застосовується кри-терій розподілу Стьюдента  , який вираховується за формулою:
, який вираховується за формулою: (11)
(11) відповідно числа ступенів свободи
відповідно числа ступенів свободи  , яке вираховується за формулою:
, яке вираховується за формулою: ,
, – кількість респондентів.
– кількість респондентів.
 , маємо констатувати, що коефіцієнт кореляції є значущим, і лише у 5% випадків може виявитися рівним 0. Зауважимо, що, якщо зазначена нерівність стверджується для
, маємо констатувати, що коефіцієнт кореляції є значущим, і лише у 5% випадків може виявитися рівним 0. Зауважимо, що, якщо зазначена нерівність стверджується для  , то значущість коефіцієнта кореляції суттєво збільшується: лише 1% випадків він може виявитися рівним 0.
, то значущість коефіцієнта кореляції суттєво збільшується: лише 1% випадків він може виявитися рівним 0. , необхідно вико-ристовувати
, необхідно вико-ристовувати  - критерій:
- критерій: (12)
(12) ;
;  .
. .
. . Через те, що
. Через те, що 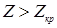 , маємо констатувати, що коефіцієнт кореляції
, маємо констатувати, що коефіцієнт кореляції  є значущим, і лише в 1% випадків може виявитися рівним 0.
є значущим, і лише в 1% випадків може виявитися рівним 0.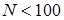 , значущість коефіцієнта кореляції можна визна-чити за таблицею, де наведено критичні значення величини
, значущість коефіцієнта кореляції можна визна-чити за таблицею, де наведено критичні значення величини  .
. (менше 100), за таблицями визначаємо, що для того, щоб
(менше 100), за таблицями визначаємо, що для того, щоб  , то критичні значення знаходяться за таблицею t – розподілення Стьюдента. Емпіричні значення критерію Z вираховуються за формулою:
, то критичні значення знаходяться за таблицею t – розподілення Стьюдента. Емпіричні значення критерію Z вираховуються за формулою: , (13)
, (13)


