Энергия Гиббса и направление химических реакций.

 

Биохимические реакции обычно происходят при изобарно- изотермических условиях. В этих условиях энергетическое состояние системы характеризуется энтальпией, а мерой неупорядоченности системы будет произведение температуры и энтропии. Функцией, учитывающей обе эти характеристики и противоположность в тенденции их изменения при самопроизвольных процессах, является свободная энергия Гиббса.

Энергия Гиббса (или изобарно – изотермический потенциал) является обобщенной функцией состояния системы, учитывающей энергетику и неупорядоченность системы при изобарно – изотермических условиях.

Названа она в честь одного из основателей химической термодинамики, американского ученого Джозайи Уилларда Гиббса (1839 – 1903).

Изменение энергии Гиббса для биохимических процессов в условиях, отличных от стандартных, можно рассчитать на основе экспериментальных значений ∆Н и ∆S для этих процессов по уравнению:

∆G =∆Н - Т∆S,

где ∆Н - характеризует полное изменение энергии системы при p,T = const и отражает стремление системы к минимуму энергии (энтальпийный фактор);

Т∆S – характеризует ту часть энергии, которую нельзя превратить в работу, и отражает стремление системы к максимуму неупорядоченности (энтропийный фактор);

∆G – характеризует ту часть энергии, которую можно перевести в работу, и является термодинамическим критерием самопроизвольного протекания любых процессов при p,T = const.

Если в уравнение для расчета свободной энергии Гиббса ввести значение ∆Н°_р. и ∆S°_р., найденные с использованием следствия из закона Гесса, то мы получаем формулу для расчета ∆G реакции, протекающей в стандартных условиях:

 

∆G°_p.f=∑ν_j∆G°_j - ∑ν_i∆G°_i

 

где∆G°_j, ∆G°_i – значения энергии Гиббса продуктов реакции и исходных веществ, ν_j,ν_i - соответствующие стехиометрические коэффициенты в уравнении химической реакции.

В термодинамических расчетах используют значения энергии Гиббса, измеренные при стандартных условиях (∆G°, кДж/моль). Данные величины приведены в справочниках термодинамических величин. Для простых веществ в термодинамически устойчивой форме стандартная энергия Гиббса их образования принята равной нулю.

Таблица 12.

 

Значение ∆G°_{f 298} некоторых соединений.

 

Молекулярная формула	∆G°f 298, кДж/моль	Молекулярная формула	∆G°f 298, кДж/моль
О2 (г)		HF(г)	-275.41
НCl(г)	-95.3	HI(г)	1.58
H2O(ж)	-228.61	CH4 (г)	-50.85
CO2(г)	-394.37	C6H6(ж)	124.38
CO(г)	-137.15	NO2 (г)	52.29
NO(г)	87.58	NH3 (г)	-16.48
HCN(г)	121.58	NaСl(кр.)	-384.13

 

Рассчитав ∆G химической реакции, можно не производя экспериментов, дать ответ о принципиальной (термодинамической) возможности (или невозможности) ее протекания:

∆G<0 – реакция протекает самопроизвольно;

∆G=0 – реакция находится в состоянии равновесия;

∆G>0 – несамопроизвольная реакция (самопроизвольна обратная реакция).

Знак ∆G, а значит, и самопроизвольность реакции зависит от величины соотношения ∆Н и Т∆S. Самопроизвольное осуществление реакции (∆G<0) возможно в следующих случаях:

 

1) ∆Н<0 (экзотермический процесс) и в то же время |∆Н |>| Т∆S |, т.е. при экзотермических процессах знаки ∆Н и ∆G совпадают, что означает возможность протекания процесса независимо от знака ∆S;

2) ∆Н>0 (эндотермический процесс) и |∆Н |<| Т∆S |, тогда возрастание энтальпии компенсируется значительно большим ростом энтропийного фактора, что осуществимо при высоких температурах или при реакциях с участием газовой фазы, когда наблюдается значительное увеличение энтропии. Этим и объясняется возможность протекания эндотермических реакций, что не согласуется с принципом Бертло о самопроизвольности только экзотермических реакций. Судить о направлении процесса по знаку изменения энтальпии в соответствии с этим признаком можно лишь: а) при низких температурах (при Т→0, Т∆S→0, и Т∆S<< ∆Н), когда знаки изменения свободной энергии и энтальпии совпадают; б) в конденсированных системах, в которых в процессе взаимодействия энтропия меняется незначительно, (беспорядок не может существенно возрасти, если, например, одно кристаллическое вещество превращается в другое кристаллическое вещество). Поэтому при низких температурах и в конденсированных системах возможно лишь протекание экзотермических реакций (∆G<0, когда ∆Н<0).

 

 

Возможность протекания реакции в зависимости от знака ∆Н и ∆S и температуры суммарно можно выразить в таблице:

 

Таблица 13.

 

Знак ∆Н	Знак ∆S	Знак ∆G	Самопроизвольность реакции	Пример
-	+	Всегда «-»	Самопроизвольна при любых температурах	2О3 (г)→ 3О2 (г)
+	-	Всегда «+»	Несамопроизвольна при любых температурах	3О2 (г)→2О3 (г)
-	-	«-» при низких температурах «+» при высоких температурах	Самопроизвольна при низких температурах, несамопроизвольна при высоких температурах	2Н2 (г)+О2 (г)→ →2Н2О(г)
+	+	«+» при низких температурах, «-» при высоких температурах	Несамопроизвольна при низких температурах, самопроизвольна при высоких температурах	2Н2О(г)→ →2Н2 (г)+О2 (г)

 

Второй закон термодинамики для любых систем формулируется следующим образом:

В системе при постоянной температуре и давлении самопроизвольно могут совершаться только такие процессы, в результате которых энергия Гиббса уменьшается, т.е. ΔG_кон > ΔG_нач, или ΔG < 0.

Для закрытых термодинамических систем наряду со свободной энергией Гиббса ∆G (изобарно-изотермический потенциал) в изохорных условиях (V = const) применяют функцию состояния системы энергию Гельмгольца (F) (изохорно– изотермический потенциал ). В химии энергия Гиббса имеет более широкое применение, чем энергия Гельмгольца, так как химические процессы чаще протекают при постоянном давлении, а не при постоянном объеме.

Энергия Гельмгольца находится по формуле:

F = U – T∙S, где U- внутренняя энергия системы

Энергия Гельмгольца характеризует работоспособность системы, т.е. определяет ту часть энергии, которая в изохорно-изотермическом процессе превращается в работу.

Энергию Гиббса можно выразить через энергию Гельмгольца следующим образом:

 

G = U + pV – TS = F + pV

Оба рассмотренных термодинамических потенциала являются функциями состояния, зависят от природы веществ – участников реакции, их массы и температуры. Кроме того, энергия Гиббса зависит от давления, а энергия Гельмгольца – от объема системы. Абсолютные значения термодинамических потенциалов неизвестны, а для расчетов пользуются обычно изменениями потенциалов (∆G и ∆F).

 

Химическое равновесие.

Химические реакции бывают обратимыми и необратимыми.

Необратимыми называются реакции, которые протекают только в одном направлении до полного израсходования одного из реагирующих веществ.

2Ca + O₂→2CaO _(тв.)

Ca + H₂SO_{4 (разб.)}→ CaSO₄+H₂↑

4Ca +5 H₂SO_{4 (конц.)}→ 4CaSO₄+H₂S +4H₂O

NH₄NO₃→ 2H₂O +N₂O↑

Критериями необратимости процесса можно считать выделение газа в процессе реакции, образование твердых и малодиссоциирующих соединений.

Однако в природе необратимых реакций меньше, чем обратимых.

Обратимыми называются процессы, в которых одновременно протекают две взаимно противоположные реакции – прямая и обратная. Например,

H₂ + I₂ ↔2HI

CH₃COOH + C₂H₅OH ↔ CH₃COOC₂H₅ + H₂O

Главная особенность протекания обратимых реакций заключается в стремлении достичь динамического равновесия, так как это состояние возникает и поддерживается вследствие протекания реакций в двух противоположных направлениях с одинаковыми скоростями.

Химическое равновесное состояние системы характеризуется:

 

1) равенством скоростей прямой и обратной реакции V_пр. = V_обр.;

2) энергетической выгодностью G_равн. = min;

3) отсутствием изменений величин параметров и функций состояния системы: концентрации реагентов, энтальпии, энтропии и энергии Гиббса для прямой и обратной реакций.

 

Поскольку в состоянии химического равновесия система достигает минимально возможного значения энергии Гиббса, то реакция, которая приводит в данных условиях к состоянию равновесия, всегда самопроизвольна. Рассмотрим на графике изменение энергии Гиббса в закрытой системе в обратимой химической реакции (р, Т=const):

В этом случае изменение энергии Гиббса в системе характеризуется минимальным значением, к которому возможен подход, как со стороны исходных веществ, так и со стороны продуктов реакции.

Так как в состоянии равновесия скорости прямой и обратной реакции равны, то, используя закон действующих масс, выразим значение скоростей прямой (V₁) и обратной реакций (V₂):

aА +bB ↔ cC + dD

V_{прям. р.}=k∙[A]^a∙[B]^b, V_{обрат. р.}=k∙[C]^c∙[D]^d

Где [A],[B],[C],[D] – равновесные концентрации реагентов и продуктов обратимой реакции, a,b,c,d – стехиометрические коэффициенты в уравнении реакции.

 

Равновесными концентрациями называются концентрации всех веществ системы, которые устанавливаются в ней при наступлении состояния химического равновесия.

Соотнеся скорости обратной и прямой реакции, получаем:

V₂ k∙[C]^c∙[D]^d

----- = -------------

V₁ k∙[A]^a∙[B]^b

 

Так как рассматриваемые реакции являются противоположными друг другу, то и значение отношения констант их скоростей и равновесных концентраций реагентов и продуктов реакции есть величина постоянная.

[C]^c∙[D]^d

К_с= ------------

[A]^a∙[B]^b

(для реакции aA + bB↔ cC +dD)

Величина К_с, равная отношению произведений равновесных концентраций к произведению равновесных концентраций реагентов, взятых в степени их стехиометрических коэффициентов, называется константой равновесия обратимой реакции.

Константа химического равновесия (К_с) обратимого процесса равна отношению произведения равновесных концентраций конечных продуктов к произведению равновесных концентраций исходных веществ в степени, равной стехиометрическим коэффициентам соответствующих химических веществ в химической реакции.

Константа равновесия (К_р) для обратимых реакций, проходящих в газовой фазе, может быть также выражена отношением произведений парциального давления продуктов реакции к произведению парциального давления реагентов, взятых в степени их стехиометрических коэффициентов.

Например, для реакции:

N_{2 (г)} + 3H_{2 (г)} ↔ 2NH_{3 (г)}

 

Константы равновесия могут быть записаны следующим образом:

Р² (NH₃) [NH₃]²

K_p= -------------- К_с = -------------

P(N₂)∙P³(H₂) [N₂]∙[H₂]³

Связь между константами равновесия, выраженными через величины парциального давления и равновесных концентраций реагентов и продуктов реакции, отражена в формуле:

К_р = К_с∙(RT) ^∆ν

где ∆ν =Σ ν_прод. - Σ ν_исх.

В случае гетерогенных реакций в выражение константы химического равновесия входят парциальные давления (или концентрации) только газообразных участников реакции. Парциальные давления и концентрации веществ в твердом и жидком состояниях принимаются за единицу, так как их химические потенциалы равны. Например, для реакции

С _(тв.) + О_{2 (г.)}↔ СО_{2 (г.)}

 

V^→ =k∙[O₂] V^← = k∙[CO₂]

[CO₂]

K_c = ---------

[O₂]

Для выражения константы равновесия (К_а) обратимых реакций растворов электролитов, значения равновесных концентраций заменяют на равновесные активности:

a_C^c ∙ a_D^d

К_а= ------------

a_A^a ∙ a_B^b

где а = С(х)∙γ, γ – коэффициент активности

(для реакции aA + bB↔ cC +dD)

 

Значение константы равновесия определяет положение равновесия, т.е. относительное содержание исходных веществ и конечных продуктов реакции, находящейся в состоянии равновесия.

Если К_с> 1,то в системе выше содержание конечных продуктов реакции, т.е. положение равновесия смещено в сторону прямой реакции.

Если К_с< 1, то в системе выше содержание исходных веществ, т.е. положение равновесия смещено в сторону обратной реакции.

Величина изменения свободной энергии Гиббса (∆G°) связана с константой равновесия обратимой реакции уравнением, выведенным Вант Гоффом в 1885 г. Он доказал, что между константой равновесия и энергией Гиббса обратимой реакции существует логарифмическая зависимость:

∆G_р. = - R∙T∙ln K_c,

где R – универсальная газовая постоянная, Т – температура (К).

Для упрощения математических расчетов зависимость константы равновесия и энергии Гиббса можно записать следующим образом:

∆G_р. = - 2,303∙R∙T∙lg K_c

Это уравнение дает возможность, зная ∆G, вычислить константу равновесия, и, наоборот, по экспериментально найденному значению константы равновесия рассчитать ∆G реакции.

Пользуясь уравнением изотермы химической реакции:

[C]^c∙[D]^d

∆G = ∆G^° + RTln ----------

[A]^a∙[B]^b

(для реакции aA + bB↔ cC +dD)

 

можно определить, в каком направлении и до какого предела может протекать реакция в конкретных условиях при заданном составе исходных реагентов и продуктов реакции. Это же уравнение позволяет определить, какими должны быть условия реакции и состав исходной смеси, чтобы реакция протекала в нужном направлении и до рассчитанного предела.

Константы равновесия обратимых реакций зависят от температуры и природы реагирующих веществ, но не зависят от концентрации (К_с), активности (К_а), давления (К_р) реагирующих веществ.

Таким образом, в случае протекания обратимых реакций система самопроизвольно приходит к состоянию химического равновесия, из которого она без внешнего воздействия не может выйти, поскольку это требует увеличения энергии Гиббса.

Влияние изменения условий на химическое равновесие определяется принципом Ле Шателье:

Если на систему, находящуюся в состоянии химического равновесия, оказывать воздействие путем изменения концентрации реагентов, давления и температуры в системе, то равновесие всегда смещается в направлении той реакции, протекание которой ослабляет это воздействие.

Влияние изменения концентрации реагентов. В соответствии с принципом Ле Шателье введение в равновесную систему дополнительных количеств какого-либо реагента вызывает сдвиг равновесия в том направлении, при котором его концентрация уменьшается. Поэтому избыток исходного вещества (исходных веществ) вызывает смещение равновесия вправо, увеличивая степень превращения других реагентов; добавление продукта (продуктов) реакции вызывает смещение равновесия влево, т.е. уменьшение степени полноты ее протекания. Так, избыток кислорода увеличивает степень превращения SO₂ в SO₃ при контактном получении триоксида серы – возрастание концентрации молекул веществ ускоряет ту реакцию, которая их израсходует. В целях повышения выхода продуктов реакции, во многих случаях смещение равновесия в сторону продуктов взаимодействия можно осуществить и их удалением из реакционной зоны, связывая их в малодиссоциирующие, труднорастворимые или нелетучие вещества. Так, введение в равновесную систему:

 

СН₃СООН + СН₃ОН ↔ СН₃СООСН₃ + Н₂О

 

водоотнимающих веществ (например, Н₂SO₄) позволяет сместить равновесие этой реакции вправо, т.е. в сторону образования продуктов реакции.

Таким образом, при изменении в равновесной системе концентрации любого из реагентов, исходное соотношение концентраций реагентов и величина константы равновесия в состоянии последующего равновесия не изменятся, хотя положение равновесия сместится в ту или иную сторону.

 

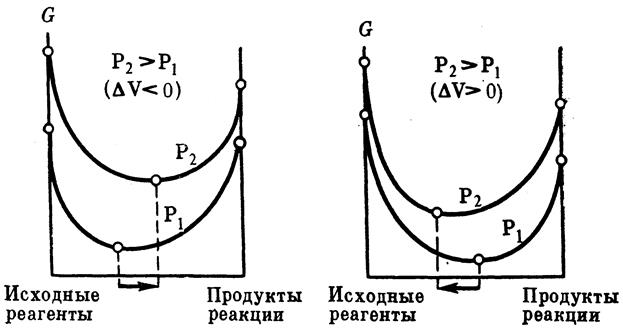
Влияние изменения давления в системе. Давление не изменяет величины константы равновесия обратимой реакции, так как она зависит только от температуры и природы реагирующих веществ, следовательно, с давлением меняется ∆G реакции.

Повышение давления в системе смещает химическое равновесие в направлении реакции, идущей с образованием меньшего числа молей газообразных веществ, т.е. в сторону уменьшения объема, а понижение давления в системе вызывает сдвиг равновесия в противоположную сторону. При равном числе молей газообразных исходных веществ и продуктов реакции изменение давления не смещает химическое равновесие. Влияние давления на химическое равновесие при Т = const показано схемой, где в первом случае рассмотрена реакция, сопровождающаяся уменьшением объема; а во втором – реакция, сопровождающаяся увеличением объема.

Чем меньше абсолютное значение изменения объема в системе, тем меньше влияние давления на равновесие. Поэтому при небольших значениях давления оно не влияет на равновесие системы. В гетерогенных процессах объемом конденсированной фазы можно пренебречь, однако, при сверхвысоких давлениях объем газов становится соизмеримым с объемом твердых тел и жидкостей. Если рассматривать реакции, в которых среди реагентов нет газообразных продуктов, например, процесс модификационного превращения С_{(графит)}→С_(алмаз), так как в данном случае изменение объема ничтожно мало, то даже для незначительного сдвига равновесия вправо требуется весьма значительное изменение (повышение) давления.

 

 

Для точного учета влияния давления на равновесие реакций, особенно при высоких давлениях, следует принимать во внимание изменение величины объема с давлением; так, если по мере повышения давления абсолютное значение изменения объема уменьшается, то будет уменьшаться и эффект действия давления в системе.

 

Влияние изменения температуры в системе. В соответствии с принципом Ле Шателье нагревание вызывает смещение равновесия в сторону того из двух встречных процессов, протекание которого сопровождается поглощением теплоты, т.е. в сторону эндотермической реакции. Понижение температуры приводит к противоположному эффекту: равновесие смещается в сторону того процесса, протекание которого сопровождается выделением тепла, в сторону экзотермической реакции. Из этого следует, что для суждения о влиянии температуры необходимо знать тепловой эффект изучаемого процесса. Как уже говорилось ранее, тепловой эффект реакции может быть определен опытным путем или по закону Гесса. Направление смещения и его степень определяются знаком и величиной теплового эффекта; чем больше ∆Н, тем значительнее влияние температуры; наоборот, если ∆Н близко к нулю, то и температура практически не влияет на равновесие. На схеме, представленной ниже, отражено влияние температуры на химическое равновесие при р = const, где первая зависимость приведена для эндотермической реакции, вторая – для экзотермической реакции.

Законы наступления, сохранения и смещения динамического равновесия справедливы не только для химических и физико-химических процессов, но и имеют аналоги в живой природе. Так устойчивость эмали зуба к кариесу определяется соотношением двух динамических процессов: де- и реминерализации, которые постоянно происходят в зубах. Реминерализация поверхностей эмали осуществляется в основном минеральными компонентами слюны, зависит от ее состава, рН и многих других факторов. При равновесии указанных процессов эмаль остается резистентной к кариесогенным влияниям.

 

 

Повышение скорости процесса деминерализации или снижение активности реминерализации нарушает динамическое равновесие, и эмаль теряет минеральные компоненты. С целью профилактики кариеса проводят искусственную реминерализацию средствами, содержащими ионы, необходимые для восстановления и укрепления зубной эмали. Т.о. равновесие в нужную сторону сдвигается за счет концентрационного фактора.

Соблюдение принципа динамического равновесия в живых системах позволяет им поддерживать состояние гомеостаза. Основу гомеостаза составляет стационарное состояние системы, причем далекое от равновесия, из-за чего живые системы способны к эволюции.

Основы биоэнергетики.

 

Протекание жизненных процессов требует затрат энергии. Источником энергии для живых организмов служит пища. Главными компонентами пищи являются жиры, белки и углеводы, окисление которых сопровождается выделением энергии. В медицине энергетическую характеристику продуктов питания принято считать в калориях. Поскольку пища – разнородная смесь, ее калорийность, как правило, приводят в виде средних значений на 100 г.

Калорийностью питательных веществ – называется энергия, выделяемая при полном окислении (сгорании) 1 г. питательных веществ.

Взаимосвязь между единицами энергии выражается соответствием:

1 калория = 4.18 Дж

Хорошо известная всем калорийность пищевых продуктов – не что иное, как теплота их сгорания, которую можно измерить экспериментально.

Начало таким измерениям положили Антуан Лавуазье и Пьер Симон в 1780 г. Определяя при помощи калориметра количество теплоты, выделенное морской свинкой, они установили, что окисление пищи в организме и вне его, дает близкие тепловые эффекты. На основании этих опытов был сделан важный вывод: живой организм выделяет теплоту за счет окисления в нем пищи кислородом воздуха. Это позволило объяснить различие в цвете артериальной и венозной крови, а в дальнейшем послужило исходным пунктом к открытию первого закона термодинамики.

Конечно, окисление питательных веществ в организме протекает совсем не так, как в калориметре. Это сложные многостадийные процессы с участием биологических катализаторов (ферментов). Однако, согласно закону Гесса, теплота, выделяемая при окислении питательных веществ, не зависит от того, окисляется она в организме или в калориметре, если продукты ее окисления одинаковы. Наибольшую энергетическую ценность имеют жиры, при окислении которых выделяется 37.7 –39.8 кДж/г (9.3 ккал/г). В процессе усвоения углеводов в организме человека выделяется 16.5 –17.2 кДж/г (4.1 ккал/г). На этом же уровне находится и калорийность белков.

Информация о выделении теплоты очень важна для понимания путей преобразования различных веществ в энергию в живых организмах. Изучение трансформации энергии в живых системах является предметом биоэнергетики.

В основе научной диетологии лежит соответствие калорийности пищевого рациона энергозатратам человека. Биоэнергетику организма можно регулировать не только с помощью выбора отдельных продуктов, но, главным образом, их сочетанием.

Зная основные термодинамические закономерности, химический состав продуктов питания и энергетические характеристики питательных веществ, врач должен уметь с учетом суточной потребности человека в энергии и на основе энергетического баланса его жизнедеятельности составить оптимальный рацион питания (энергоменю) для различных групп людей (дети, школьники, работающие мужчины и женщины, студенты и т.д.).

 

 

Лабораторный практикум.

 

Количество теплоты измеряют по ее переносу от одного тела к другому. Повышение температуры тела определяется теплоемкостью:

С = Q/∆T,

Где С – теплоемкость, Q – количество теплоты, полученной телом, ∆Т – изменение температуры тела.

Соответственно, зная теплоемкость и изменение температуры, можно рассчитать количество теплоты, полученное или выделенное телом.

Тепловые эффекты реакций измеряют с помощью специальных приборов – калориметров. Этот термин предложили в 1780 г. французские ученые Антуан Лоран Лавуазье и Пьер Симон Лаплас. Основоположником калориметрии считается английский химик Джозеф Блэк, известный своими работами о природе теплоты.

Простейший калориметр – теплоизолированный сосуд с водой, снабженный мешалкой и термометром. Контейнер, в котором протекает исследуемый процесс (например, химическая реакция), помещают в калориметр и регистрируют изменение температуры воды. Зная теплоемкость калориметра, рассчитывают количество выделившейся теплоты. На рисунке представлена схема строения пламенного калориметра.

 

ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ ТЕПЛОВЫХ ЭФФЕКТОВ.

 

Определение тепловых эффектов химических процессов является задачей термохимии. Термохимические методы имеют большое значение не только в химических, но и в медико-биологических науках. Энергия, необходимая живым организмам для совершения работы, поддержания постоянной температуры тела и т.д., получается организмом за счет экзотермических реакций окисления, протекающих в клетках.

В химических лабораториях применяется простейший калориметр, который состоит из сосуда для проведения химической реакции, помещенного во внешнюю оболочку. Калориметр снабжен термометром, мешалкой для быстрого достижения однородности раствора, и воронкой для введения в сосуд растворов реагирующих веществ. Количество теплоты, выделяющейся или поглощающейся в калориметре, определяют по общей теплоемкости всех частей калориметра и изменению температуры.

 

РАБОТА № 1. Определение теплоты реакции нейтрализации сильной кислоты сильным основанием.

 

Цель работы: научиться определять теплоту реакции нейтрализации сильной кислоты сильным основанием.

Теплотой нейтрализации называется количество теплоты, которое выделяется при взаимодействии моль-эквивалента кислоты с моль-эквивалентом основания. Нейтрализация 1 моль-экв. сильной кислоты сильным основанием, в достаточно разбавленном растворе, сопровождается почти одинаковым экзотермическим тепловым эффектом, отвечающим одному и тому же процессу – образованием 1 моля жидкой воды из гидратированных ионов по уравнению:

H⁺_aq + OH^-_aq → H₂O(ж), Q_нейт.= 55.9 кДж/моль.

Постоянство теплоты нейтрализации не соблюдается при нейтрализации слабого основания сильной кислотой или наоборот, так как в этих реакциях на тепловой эффект реакции влияет теплота диссоциации слабого электролита.

Выполнение работы. Во взвешенный калориметрический стакан помещают 50 мл 1.0 N раствора щелочи и записывают показание термометра. В отдельный стакан отмеряют 60 мл 1.0 N раствора соляной кислоты и измеряют его температуру. Поместив мешалку и термометр в калориметрический стакан, его закрывают крышкой. Затем, при перемешивании, вливают через воронку раствор кислоты в калориметр и следят за показаниями термометра, отмечая самую высокую температуру.

Результаты опыта записывают в таблицу:

 

Масса калориметрического стакана, m1, г.
Концентрация растворов, моль/л
Объем раствора щелочи, V1, мл
Объем раствора кислоты, V2, мл
Температура щелочи, tºщ.
Температура кислоты, tºк.
Начальная температура, tº1= 0,5(tºщ.+ tºк.)
Температура после нейтрализации, tº2
Общая масса растворов m2 = ρ(V1+V2)

 

Вычисления:

1. Вычисление теплоты, выделившейся в результате реакции, производят по формуле:

q=(m₁∙c₁+m₂∙c₂) ∙(t₂ – t₁)

Удельную теплоемкость стекла (с₁) принять равной 0,753 Дж/г∙град., раствора (с₂) – 4,184 Дж/г∙град., плотность раствора (ρ) – 1 г/мл.

2. Чтобы определить теплоту нейтрализации, необходимо пересчитать выделившуюся теплоту на 1 моль - эквивалент щелочи, так как кислота взята в избытке.

Расчет производят по формуле:

Q_нейтр. = q∙1000/N_щ.∙V_щ., Дж/моль.

3. Сравнивают опытное и теоретическое значения теплоты нейтрализации и определяют (в%) относительную ошибку опыта:

% ошибки =((Q_теор. – Q_опыт.)/ Q_теор)∙100%

В отчете о работе следует кратко описать ход определения, внести результаты опыта и расчеты.

 

 

РАБОТА №2. Определение теплоты нейтрализации слабой кислоты слабым основанием.

Цель работы: научиться определять теплоту нейтрализации слабой кислоты слабым основанием, объяснить причины различия теплоты нейтрализации сильной кислоты сильным основанием и теплоты нейтрализации слабой кислоты слабым основанием.

 

Проведите опыт, описанный в работе №1, взяв 1.0 N растворы аммиака и уксусной кислоты. Вычислите теплоту нейтрализации в расчете на 1 моль - эквивалент уксусной кислоты. Сравните результаты с данными предыдущей работы.

 

 

РАБОТА №3. Определение теплоты растворения соли.

 

Цель работы: Определить интегральную теплоту растворения хлорида калия. Определить теплоту растворения и гидратации безводного хлорида кальция.

 

Интегральной теплотой растворения называют количество теплоты, выделяемой или поглощаемой при растворении 1 моля вещества в определенном объеме растворителя.

Интегральная теплота растворения электролитов определяется исходя из двух стадий данного процесса: во-первых, поглощения теплоты, которая расходуется на разрушение кристаллической решетки (Q₁), и, во-вторых, выделения теплоты вследствие гидратации или сольватации каждого иона молекулами растворителя (Q₂).

Q_раств.=-Q₁ + Q₂

Выполнение работы: Во взвешенный калориметрический стакан наливают 100 мл дистиллированной воды. Отвешивают около 2 г хорошо измельченного хлорида калия KCl с точностью до 0,01г. Записывают температуру воды в калориметре и затем, при перемешивании, через воронку прибавляют навеску соли. При растворении соли температура раствора понижается, в результаты опыта записывают ее минимальное значение.

Данные эксперимента записывают в таблицу:

 

Масса калориметрического стакана, m1, г.
Масса воды, m2, г.
Навеска соли, m3, г.
Температура воды, t1°
Температура раствора соли,t2°

 

Теплоту растворения рассчитывают, используя формулу:

Q_раств.=((t₂ – t₁)∙c∙M)/m₃

где с=c₁∙m₁ +c₂∙m₂, М – молярная масса соли.

Удельная теплоемкость стекла (с₁) и раствора (с₂) указана в работе №1. Интегральная теплота растворения хлорида калия (по таблице).

Q_раств.=-17.577 кДж/моль

 

Таким же образом проводят опыт с безводным хлоридом кальция CaCl₂. В калориметрический стакан наливают 50 мл дистиллированной воды, отвешивают около 2 г. хорошо измельченной соли с точностью до 0,01 г.

Определив теплоту растворения безводного хлорида кальция CaCl₂, вычисляют теплоту гидратации этой соли, зная теплоту растворения кристаллогидрата CaCl₂∙6H₂O (Q₂=19.08 кДж/моль).

Q_гидр.=Q_{1 р.безв.} – Q_{2 р. гидр.}

В отчете о работе кратко опишите ход определения, внесите результаты и расчеты работы.

 

РАБОТА №4. Определение теплоты гидратации карбоната натрия.

 

Опыт проводят по методике, описанной в работе №3. Навеска безводного карбоната натрия Na₂CO₃ должна составлять около 2,3 г., а кристаллогидрата карбоната натрия – около 5 г. на 100мл воды.

Определив теплоты растворения, рассчитывают теплоту гидратации безводного хлорида кальция.

Напишите термохимическое уравнение гидратации данной соли, нарисуйте треугольник Гесса для данного процесса. Какова величина энтальпии гидратации данной соли?

 

Примеры решения задач.

Задача №1. Вычислить теплоту гидратации безводной соли Na₂SO₄.

 

Решение. Гидратация солей протекает медленно и обычно приводит к образованию смеси кристаллогидратов. Теплоту гидратации можно вычислить, если известны теплоты растворения безводной соли и кристаллогидрата:

Na₂SO₄ + n Н₂О→ 2Na⁺ + SO₄ ^2- _{(раствор)}+3.02 кДж/моль

Na₂SO₄∙10 Н₂О +m Н₂О→ раствор Na₂SO₄ – 78.6 кДж/моль

Процесс растворения соли можно представить следующей схемой:

 

∆Н_р.

Na₂SO₄ + n Н₂О 2Na⁺ ₊ SO₄ ^2- _{(раствор)}

∆Н _(гидр.) ∆Н _{(раств. крист.)}

Na₂SO₄∙10 Н₂О

 

По закону Гесса: ∆Н_р =∆Н _(гидр.) +∆Н _{(раств. крист.)}.

Тогда ∆Н _(гидр.)= ∆Н_р - ∆Н _{(раств. крист.)} = 3.02 – (-78.6) = 81.62 кДж/моль.

 

 

Задача № 2. Вычислить константу равновесия реакции:

NH₃ + HCl ↔ NH₄Cl _(тв.)

 

Решение. Прежде всего, определим ∆G_р. реакции, используя следствие из закона Гесса. Находим по справочнику термодинамических величин значение ∆G веществ, входящих в уравнение реакции:

∆G_f° (NH₃) = -16.7 кДж/моль, ∆G_f° (HCl) = -95.4 кДж/моль,

∆G_f °(NH₄Cl) =-203.7 кДж/моль.

По следствию из закона Гесса: ∆G°_p.f=∑ν_j∆G°_j - ∑ν_i∆G°_I

∆G°_p.f = ∆G_f °(NH₄Cl) –(∆G_f° (NH₃) +∆G_f° (HCl)

∆G°_p.f =-203.7 –(-16.7 + (-95.4)) = -91.6 кДж,

Теперь воспользуемся уравнением, связывающим ∆G и К_с реакции:

∆G_р. = - 2,303∙R∙T∙lg K_c

∆G_р.^° = -2.303 ∙8.314∙298∙ lg K_c =-569∙lg K_c

-91.6 = -5.69∙ lg K_c

lg K_c ≈ 16, т.е. K_c = 1/[NH₃] ∙[HCl] =10¹⁶

Большое значение константы равновесия показывает, что при стандартной температуре равновесие реакции сильно смещено в сторону прямой реакции.

 

 

Задача № 3. Рассчитать будет ли протекать при 25°С реакция?

2NO₂→ N₂O₄ + 57.9 кДж/моль

Решение: Согласно термохимическому уравнению реакции:

∆Н_р.^° = - 57.9 кДж/моль

Найдем по таблице термодинамических величин значения энтропии для веществ, вхо