
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Работа 2 Установление нормальности и титра раствора тиосульфата натрия по бихромату калия.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
К определенному количеству титрованного раствора K2Cr2O7 приливают КI в кислой среде. Выделившийся йод оттитровывают раствором тиосульфата натрия. Реакции протекают по уравнению:
Ход определения Приступая к титрованию, наполняют бюретки раствором Na2S2O3 и устанавливают уровень жидкости в ней на 0. В колбу для титрования мерным цилиндром или градуированной пробиркой вносят 1-2 мл 5%-ного раствора КI и 2-3 мл 1н раствора H2SO4. Затем к полученной смеси пипеткой Мора добавляют 5 мл 0,02н раствора K2Cr2O7 (кончик пипетки при этом не должен касаться смеси). Полученную смесь слегка перемешивают, колбу закрывают часовым или предметным стеклом, чтобы предупредить потери от улетучивания йода и оставляют для завершения реакции на 5 минут. Выделившийся йод титруют тиосульфатом натрия (Na2S2O3) до светло-желтой окраски, затем прибавляют 4-5 капель крахмала и продолжают титровать до перехода синей окраски в бледно-зеленую (или бесцветную) от одной капли раствора тиосульфата натрия. Последние капли прибавляют медленно, хорошо перемешивая раствор. Титрование повторяют 2-3 раза. Из полученных результатов (разность не более 0,1 мл) берут среднее значение для расчетов. Данные заносят в таблицу.
Таблица 8.
§6. Задачи для самостоятельного решения. 1. Укажите, какие из приведенных процессов представляют собой окисление и какие – восстановление:
2. Расставьте коэффициенты в уравнениях следующих реакций:
3. Закончите уравнения реакций и расставьте коэффициенты:
4.Рассчитайте навеску KMnO4, необходимую для приготовления 1 л 0,02н раствора 5.На титрование 4,5 мл 0,1н раствора щавелевой кислоты израсходовано 55 мл KMnO4. Рассчитайте нормальность и титр раствора KMnO4.
Глава IV. ХИМИЧЕСКАЯ ТЕРМОДИНАМИКА
«Каким бы ни было исследуемое вещество, термохимия открывает новые возможности для наших исследований. Она по своей природе является для химии тем же, чем микроскоп для натуралиста, подзорная труба для астронома». Г.И.Гесс Вопросы к занятию 1. Основные понятия термодинамики: система, процесс, параметры, функции.
2. Первое начало термодинамики. Энтальпия. 3. Закон Гесса и следствия из него. 4. Второе начало термодинамики. Энтропия. 5. Энергия Гиббса. Критерии самопроизвольности процессов: энтальпийный и энтропийный факторы. 6. Химическое и термодинамическое равновесия. 7. Биоэнергетика. Основные понятия термодинамики. Термодинамика изучает законы, которые описывают энергетические превращения, сопровождающие физические, химические и биологические процессы. Процесс – это переход системы из одного состояния в другое, сопровождающийся необратимым или обратимым изменением хотя бы одного параметра, характеризующего данную систему. Термодинамика изучает все объекты, рассматривая их особой структурой, называемой системой. Системой называют тело или группу взаимодействующих тел, фактически или мысленно выделяемых из окружающей среды. Исходя из характера взаимодействия различных систем с окружающей средой, их подразделяют на открытые, закрытые и изолированные системы. Открытая система обменивается с окружающей средой энергией и веществом (Δm ≠ 0; ΔQ ≠ 0). Закрытой называют систему, в которой отсутствует обмен вещества с окружающей средой, но она может обмениваться с ней энергией (Δm = 0; ΔQ ≠ 0). Изолированная система характеризуется отсутствием обмена энергией и веществом с окружающей средой (Δm = 0; ΔQ = 0). Понятие изолированная система является идеальным (абстрактным), так как на практике не существует материала, который абсолютно не проводил бы теплоту. Таким образом, абсолютно изолированных систем в природе нет. Система может быть гомогенной (однородной) или гетерогенной (неоднородной). Система является гомогенной, если все ее составные части находятся в одном агрегатном состоянии, т. е. между ними отсутствует поверхность раздела. Примером такой системы является плазма крови. В гетерогенной системе можно выделить поверхность раздела между различными составляющими этой системы, таким системам характерна неоднородность, они содержат несколько фаз. Фаза – однородная часть системы с одинаковыми химическими и термодинамическими свойствами, отделенная от других частей видимой поверхностью раздела, при переходе через которую физические и химические свойства резко изменяются. Различные биологические объекты, такие как, человек или клетки живых организмов, являются примерами гетерогенных систем.
Реакции, протекающие в гомогенной системе, развиваются во всем ее объеме, и называются гомогенными. Реакции, происходящие на границе раздела фаз, называются гетерогенными. Совокупность всех физических и химических свойств системы называется состоянием системы. Состояние системы характеризуется параметрами, которые подразделяются на экстенсивные и интенсивные. Экстенсивные параметры – параметры, значения которых пропорциональны числу частиц в системе (масса, объем, количество вещества). Интенсивные параметры – параметры, значения которых не зависят от количества частиц в системе (температура, плотность (p), давление). При взаимодействии двух систем интенсивные параметры усредняют, а экстенсивные – складывают.Изменение параметра обозначают греческой буквой Δ (дельта), например ΔТ. Параметры, описывающие состояние системы, называются функциями. Одним из свойств любой функции состояния является независимость ее изменения от способа, или, как говорят, от пути реализации процесса. Функции состояния могут быть использованы для создания уравнения, описывающего термодинамический процесс (закон Бойля - Мариотта, уравнение Клайперона-Менделеева). Эти уравнения позволяют описать конкретный термодинамический процесс, что и является конечной целью термодинамики. §2. Первый закон термодинамики. Энтальпия.
В 1840 г. немецкий врач Юлиус Роберт Майер (1814 – 1878) работал на острове Ява. В те годы обычной медицинской процедурой было кровопускание. Майер обратил внимание на то, что венозная кровь матросов, которых он лечил, светлее, чем была в северных широтах, и близка по цвету артериальной. Майер знал: изменение окраски крови связано с поглощением кислорода (насыщенная кислородом артериальная кровь светлее лишенной кислорода венозной). Ученый смог дать правильное объяснение обнаруженному им явлению. В жарком климате для поддержания постоянной температуры тела организм должен вырабатывать меньше теплоты, поэтому на окисление пищи расходуется меньше кислорода и кровь почти не темнеет. В 1842 г. Майер сформулировал важнейший для термодинамики вывод о том, что теплота и работа могут превращаться друг в друга. Кроме того, он впервые установил количественное соотношение между теплотой и работой, вычислив так называемый механический эквиваленттеплоты. Формулирование первого закона термодинамики завершил в 1850 г. немецкий физик Рудольф Юлиус Эмануэль Клаузиус (1822-1888). Из принципа эквивалентности теплоты и работы, заключил он, следует, что система обладает особым свойством, изменение которого равно алгебраической сумме теплоты и работы. Позднее это свойство получило название внутренней энергии (U). Одна из основных функций состояния системы – полная энергия системы Е, которая представляет собой сумму трех составляющих: кинетической энергии Екин. движущейся системы, потенциальной энергии Епот., обусловленной воздействием на систему внешних силовых полей, и внутренней энергии системы U: Е=Екин. + Епот. + U При термодинамическом описании предполагают, что система находится в состоянии относительного покоя (Екин.=0) и воздействие внешних полей пренебрежимо мало (Епот.=0). Тогда полная энергия системы определяется запасом ее внутренней энергии (Е=U). Для термодинамического анализа характеристической величиной является изменение внутренней энергии при переходе системы из одного состояния в другое. Внутренняя энергия, как и любое термодинамическое свойство системы, является функцией состояния, т.е. изменение ее не будет зависеть от того, через какие промежуточные стадии идет процесс, а будет определяться только исходным и конечным состоянием системы. Это положение вытекает из закона сохранения энергии, согласно которому энергия не исчезает и не возникает вновь, а лишь переходит из одной формы в другую в строго эквивалентных соотношениях. В соответствии с этим законом, выражающим первое начало термодинамики, общий запас внутренней энергии остается постоянным, если отсутствует тепловой обмен с окружающей средой, т.е. в изолированных системах, в ходе процессов возможно лишь перераспределение внутренней энергии между отдельными составляющими системы.
Первый закон термодинамики является частным случаем закона сохранения энергии применительно к макроскопическим системам. Согласно первому закону термодинамики Сообщенная системе теплота расходуется на приращение внутренней энергии и на совершение работы против внешних сил: Q=∆U +A Уравнение представляет собой математическое выражение первого начала термодинамики. Выражение «работы против внешних сил», в частности, против внешнего давления, в изобарно-изотермических условиях, в которых функционируют живые организмы, может быть записано:
А=p∙∆V, тогда Q=∆U+p∆V=(U2 –U1) + p∙(V2 – V1)=(U2+pV2) – (U1+pV1) Через U1,U2 обозначен запас внутренней энергии в исходном и конечном состояниях, V1,V2 – значения объема в исходном и конечном состояниях системы. Вводя функцию состояния системы Н=U +pV, называемую энтальпией (теплосодержанием) системы, получаем: Q=H2 – H1=∆H Название энтальпия (от греч. «энтальпо» - «нагреваю») ввел нидерландский физик Хейке Камерлинг – Оннес (1853 – 1926). Количество теплоты, которое выделяется или поглощается при проведении химических реакций в изобарно-изотермических условиях, характеризуется изменением энтальпии системы и называется энтальпией реакции ∆Нр. Химические реакции, сопровождающиеся поглощением или выделением теплоты, подразделяются на экзотермические и эндотермические. Экзотермические процессы сопровождаются выделением энергии из системы в окружающую среду. В результате таких процессов энтальпия системы уменьшается (∆Н<0).
Эндотермические процессы сопровождаются поглощением энергии системой из окружающей среды, следовательно, энтальпия системы повышается (∆Н>0) (рис 5.)
Рис. 5. Энергетические (энтальпийные) профили реакций: а) – экзотермической; б) - эндотермической
Энтальпия системы является экстенсивным параметром и зависит от количества вещества, температуры и давления, поэтому изменение энтальпии в результате химической реакции определяют при стандартных условиях. Стандартные условия: давление – 760 мм рт. ст.=101325 Па Температура – 298 К ≈25°С Значения ∆Н зависят от природы веществ, условий их существования и от характера рассматриваемого процесса. Поэтому их принято унифицировать, относя к так называемому стандартному состоянию. Под последним подразумевают стандартные значения давления и температуры, для кристаллических и жидких веществ их устойчивое состояние при р=1 атм., а для газов их состояние под атмосферным давлением и при условии, что они обладают свойствами, присущими им при очень низких давлениях, т.е. являются идеальными газами. Для веществ в растворе принимают их концентрацию С(Х) = 1 моль/л, причем предполагается, что раствор ведет себя, как и при весьма небольших (точнее при бесконечно малых) концентрациях, т.е. является идеальным раствором. Стандартная энтальпия реакции (∆Н°р) представляет собой энергетическую характеристику химической реакции, проводимой в стандартных условиях. Химические уравнения реакции, для которых указано значение энтальпии реакции, называют термохимическими уравнениями. Например: СS2 (ж) +3О2 (г) = СО2 (г) + 2SО2 (г) + 1101.8 кДж, СаСО3 (тв) = СаО (тв) + СО2 (г) – 157.16 кДж. В термодинамических расчетах для оценки энергетического состояния веществ используют понятие стандартных энтальпий образования этих веществ. Стандартная энтальпия образования простых веществ (∆Н°298) в их наиболее термодинамически устойчивом агрегатном и аллотропном состоянии при стандартных условиях принимается равной нулю. Стандартная энтальпия образования сложного вещества (∆Н°298) равна энтальпии реакции получения 1 моль данного вещества из простых веществ при стандартных условиях. Таблица 9.
Значение стандартных теплот образования ∆Н°298, кДж/моль для некоторых веществ в газовом состоянии.
Значение стандартной энтальпии образования сложного вещества зависит от природы вещества и его агрегатного состояния. Числовые значения стандартных энтальпий образования являются справочными величинами. Закон Гесса.
Важнейшим постулатом термохимии является закон Гесса, или закон постоянства сумм тепловых эффектов реакций, установленный в 1840 г. русским химиком академиком Российской академии наук Германом Ивановичем Гессом Закон Гесса можно проиллюстрировать схемой:
А + В = АВ (∆Н)
А+С=АС (∆Н1) АС+В=АВ+С (∆Н2) АС
Образование соединения АВ представлено двумя путями: непосредственным синтезом из компонентов (∆Н) или через стадию образования промежуточного соединения АС (∆Н1), которое, реагируя с В (∆Н2) дает тот же конечный продукт. В соответствии с законом Гесса тепловой эффект прямого синтеза АВ равен сумме тепловых эффектов реакций с участием промежуточного продукта АС, т.е. ∆Н = ∆Н1 + ∆Н2. Тепловой эффект химической реакции зависит только от природы и состояния исходных веществ и конечных продуктов реакции и не зависит от пути реализации процесса, т.е. от пути перехода от начального состояния к конечному. Закон Гесса, хотя и был сформулирован раньше первого закона термодинамики, по сути, является его следствием и отражает тот факт, что тепловой эффект реакции равен изменению внутренней энергии или энтальпии, которые есть функции состояния, не зависящие от пути перехода из одного состояния в другое. Закон Гесса позволяет вычислять тепловые эффекты реакций, если по какой-либо причине это невозможно сделать экспериментально. Для этого «неизмеряемую» реакцию нужно скомбинировать из нескольких «измеряемых». Например, непосредственно измерить тепловой эффект реакции С(тв.) + 0.5О2 (г)→СО (г) при сжигании твердого углерода в эквивалентном количестве кислорода не удается, поскольку наряду с СО всегда образуется и СО2. Однако тепловой эффект данной реакции можно рассчитать, измерив его у двух других реакций: С(тв.) + О2 (г)→СО 2(г) ∆Н°=-393.5 кДж/моль
СО(г) + 0.5О2 (г) →СО 2(г) ∆Н°=-283.0 кДж/моль Вычитая из первого уравнения второе, получим искомое уравнение и искомый тепловой эффект: С (тв.) + 0.5О2 (г)→СО (г) ∆Н°=-110.5 кДж/моль.
§4. Следствия из закона Гесса.
Энтальпия реакции образования равна разности алгебраической суммы энтальпий образования всех продуктов реакции и алгебраической суммы энтальпий образования всех исходных веществ: ∆Н°p.f=∑νj∆Н°j - ∑νi∆Н°i где∆Н°j, ∆Н°i – энтальпии образования продуктов реакции и исходных веществ, νj,νi - соответствующие стехиометрические коэффициенты в уравнении химической реакции. Причем следует учесть, что ∆Н° образования простых веществ равна нулю.
Энтальпия реакции сгорания равна разности алгебраической суммы теплот сгорания исходных веществ и алгебраической суммы теплот сгорания конечных продуктов реакции: ∆Н°р.сг.=∑νi∆Н°i - ∑νj∆Н°j где ∆Н°i, ∆Н°j – теплоты сгорания исходных веществ и продуктов реакции, νi,νj - соответствующие стехиометрические коэффициенты в уравнении химической реакции. Причем следует учесть, что теплота сгорания высших оксидов (например, Н2О, СО2) принимается равной нулю.
Таблица 10. Значение стандартных теплот сгорания для некоторых веществ в газовом состоянии.
Это следствие позволяет вычислять энтальпии различных реакций (в том числе и биохимических, осуществление которых in vitro невозможно), используя табличные данные стандартных энтальпий образования продуктов реакции и исходных веществ.
Энтальпия прямой реакции численно равна энтальпии обратной реакции, но противоположна по знаку. ∆Н°пр. реакции =- ∆Н°обр. реакции Например, рассчитаем стандартную энтальпию реакции фотосинтеза глюкозы, которая является обратной реакцией горения глюкозы:
фотосинтез
горение ∆Нфотосинтеза =-∆Нгорения; ∆Нгорения (С6Н12О6 (тв))=-1273 кДж/моль ∆Нфотосинтеза (С6Н12О6 (тв))=-(-1273)=+1273 кДж/моль.
Закон Гесса и следствия, вытекающие из него, широко используется для ведения термохимических расчетов различных химических реакций. Располагая значениями тепловых эффектов образования, сгорания, растворения, парообразования и т.д., можно с помощью закона Гесса рассчитать теплоты самых разнообразных процессов, в частности таких, экспериментальное изучение которых затруднительно или вообще невозможно.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-17; просмотров: 1343; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.7.115 (0.012 с.) |

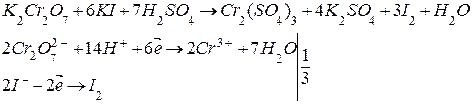
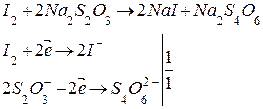














 А АВ
А АВ
 6СО2 (г) + 6Н2О(ж) С6Н12О6 (тв) +6О2 (г)
6СО2 (г) + 6Н2О(ж) С6Н12О6 (тв) +6О2 (г)


