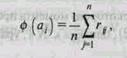Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод экспертно-аналитического анализа информации по управлению маркетингомСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Основные методы получения информации в маркетинге позволяют создать информационную основу для экспортно-аналитического анализа информации по управлению маркетингом, который включает группу методов: экспортно-аналитические, коммуникационного согласования, рефлективной диагностики и матричного позиционирования. Эскпертно-аналитические методы. Суть данных методов состоит в том, что эксперт-маркетолог, изучая какой-то конкретный экономический вопрос или явление, относящиеся к деятельности фирмы, разбивает сложное исследуемое явление на составные части, рассматривает поведение отдельных элементов и их взаимосвязи, а затем делает вывод, используя аналитические методы. К данной группе методов относится прежде всего арсенал экономико-математических методов. Различают: 1) математические методы моделирования; 2) методы прогнозирования экономических показателей поведения фирмы на рынке; 3) методы анализа маркетинговых ситуаций. Математические методы моделирования имеют целью облегчить процесс принятия решений и применяются специалистом-маркетологом для выявления особенностей функционирования экономических объектов (например, своей фирмы, главных конкурентов, потенциальных рынков и т.д.). На основе полученных результатов представляется возможным предсказывать их будущее поведение при изменении каких-либо внутренних или внешних параметров. Как правило, предсказание будущего, например изменений в руководстве государством или касающихся смены класса партнерских отношений, в значительной степени опирается на интуитивные оценки. Естественно, что при этом могут быть упущены или неверно оценены экономические показатели, влияющие на ситуацию. В данном случае использование математического моделирования позволяет оценить взаимосвязи экономических переменных через их количественные соотношения. В экономической практике моделирование необходимо для предсказания новых результатов или новых свойств исследуемого явления. При моделировании специалист-маркетолог может использовать уже полученные результаты и существующие статистические показатели или использовать данные, которых планируется достигнуть в некоторый момент в будущем.
Математические модели. Математическая модель представляет собой упрощение реальной ситуации и может не учитывать важные, реально существующие элементы деятельности фирмы, например наличие контроля, но они дают возможность маркетологу «почувствовать» поставленную задачу, и нередко еще до того, как она будет окончательно сформулирована. Затем он может включать в рассмотрение и другие факторы, пока не будет найдено приемлемое решение проблемы. В зависимости от уровня обобщения информационных данных различают: теоретические модели - используются для изучения общих свойств какого-либо явления, относящегося к деятельности фирмы, и его характерных элементов на основании выводов из формальных предпосылок; прикладные модели — позволяют оценивать параметры функционирования конкретного экономического объекта и выработать конкретные рекомендации для принятия практических решений. К ним относятся эконометрические модели. В зависимости от состояния элементов исследуемого объекта или явления различают: статические модели, описывающие состояние объекта в конкретный момент или период времени (обычно они фиксируют значения ряда величин, являющихся переменными, например капитальные ресурсы, цены и т.д.); динамические модели, включающие взаимосвязь переменных во времени. Они описывают силы и взаимодействия, влияющие на функционирование фирмы и определяющие протекание внешних и внутренних процессов ее жизнедеятельности. По определению статическое моделирование отличается от динамического тем, что в нем не рассматриваются изменения во времени. В зависимости от характера рассматриваемых переменных различают: детерминированные модели, описывающие жесткие функциональные связи между переменными; стохастические модели, допускающие наличие случайного воздействия на исследуемые показатели и использующие для его описания инструментарий теории вероятностей и математической статистики. Отметим, что в управлении маркетингом большая часть задач предполагает учет риска и неопределенности, а следовательно, их решение возможно лишь с использованием стохастических моделей. Приведенная классификация применяемых математических методов в классе решения задач по управлению маркетингом является безусловно неполной. Однако она дает возможность ориентироваться в основных типах задач по управлению маркетингом и показывает механизм их использования в зависимости от конкретной ситуации. В качестве примера рассмотрим задачу по управлению маркетингом, моделирующую ситуацию проведения в заданном регионе рекламной кампании.
Модель рекламной кампании
Фирма начинает рекламировать новый товар или услугу. Естественно, прибыль от будущих продаж должна значительно покрывать издержки на рекламную кампанию. При этом вначале расходы могут превышать прибыль, поскольку лишь малая часть потенциальных покупателей будет информирована о новинке. Затем, при увеличении числа продаж, появляется возможность рассчитывать на заметную прибыль. Наконец, наступит момент, когда рынок насытится, и рекламировать товар далее станет бессмысленно. Рассмотрим обозначенные три этапа рекламной кампании в рамках следующей модели. Пусть t — время, прошедшее с начала рекламной кампании; N 0 — общее число потенциальных платежеспособных покупателей; Nt — число уже информированных потребителей, готовых купить рекламируемый товар; α1 (t) - величина, характеризующая интенсивность рекламной кампании и фактически определяемая затратами на рекламу в данный момент времени. Предполагается, что величина
Прибыль превосходит издержки при условии pN 0> 1, и если реклама действенна и недорога, а рынок достаточно емок, то выигрыш достигается с первых же шагов рекламной кампании (в действительности между оплатой рекламы, рекламными действиями и последующей покупкой имеет место временной лаг). При не слишком эффективной или дорогой рекламе фирма на первых порах несет убытки. Однако это обстоятельство не может служить основанием для прекращения рекламы. Действительно, выражение (3) и полученное с его помощью условие pN 0 > 1 справедливы лишь при малых значениях N(t), когда функции P и S растут со временем по одинаковым законам. При увеличении N(t) опущенные в (1) члены второго порядка малости становятся заметными, в частности усиливается действие косвенной рекламы. Поэтому функция N(t) может стать более «быстрой» функцией времени, чем рассчитанная по формулам (2) и (3). Этот нелинейный эффект в изменении величины N(t) при неизменном темпе роста издержек позволяет скомпенсировать финансовую неудачу начальной стадии кампании. Поясним данное утверждение в частном случае решения уравнения (1) с постоянными коэффициентами α1 и α2. Заменой =
Его решение стремится к предельному значению 0, а функция N(t) — к N 0. В единицу времени появляется ничтожно малое число новых покупателей, и поступающая прибыль при любых условиях не может покрыть продолжающихся издержек. Рассмотренные задачи по использованию отдельных моделей в различных ситуациях еще не являются объемными и самодостаточными в сложных ситуациях управления маркетингом. Понимание наличия риска и неопределенности в каждой конкретной ситуации, с которой сталкивается управленец-маркетолог, заставляет обратить внимание на вопросы, связанные с критериальностью определения риска.
Различают несколько критериев, по которым могут приниматься решения в условиях неопределенности с применением математических методов. I. Критерий минимакса оценивает альтернативы, учитывая исключительно наихудший из всех возможных исходов, принимается та альтернатива, которая ведет в случае наихудшего исхода к наилучшему результату:
где ф (аi) - значение критерия для i -й альтернативы, rij — исход при выборе i -й альтернативы и наступлении j -го варианта обстановки. Это самый пессимистический критерий, следовательно, его скорее будет применять инвестор, стремящийся избегать малейшего риска. II. Критерий максимакса представляет собой полную противоположность критерию минимакса - принимается та альтернатива, которая ведет в случае наилучшего исхода к наилучшему результату:
Очевидно, что критерий максимакса будет использовать инвестор, склонный к максимальному, часто неоправданному риску. III. Критерий Гурвича представляет собой комбинацию критериев минимакса и максимакса и предусматривает применение коэффициента, определяющего, какой вес придается самому благоприятному и соответственно самому неблагоприятному исходу той или иной альтернативы при ее сравнении с другими альтернативами:
где δ - коэффициент критерия Гурвича (1 > δ > 0). IV. Критерий Лапласа предполагает, что все варианты экономического процесса имеют одинаковую вероятность наступления. Учитывая это предположение, рассчитывается не что иное, как математическое ожидание случайной величины rij:
где n - количество вариантов процесса. V. Критерий Сэвиджа позволяет минимизировать возможные потери после реализации ошибочной альтернативы в случае наступления неблагоприятного для этой альтернативы варианта событий. Эти потери измеряются как разница между полученным результатом и результатом, который мог бы быть получен в случае выбора альтернативы с наиболее благоприятным результатом в условиях наступившего варианта событий. Для использования этого критерия необходима трансформация исходной матрицы R в R':
где r’ij — это упущенная прибыль. Расчет критерия Сэвиджа происходит по формуле
Пример выбора альтернативы с использованием различных критериев представлен в табл. 3.11.
Таблица 3.11
|
|||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 482; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.1.58 (0.013 с.) |

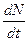 — скорость изменения со временем числа потребителей, узнавших о товаре и готовых купить его, - пропорциональна числу покупателей, еще не знающих о нем,т.е. величине
— скорость изменения со временем числа потребителей, узнавших о товаре и готовых купить его, - пропорциональна числу покупателей, еще не знающих о нем,т.е. величине
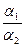 + N оно сводится к уравнению
+ N оно сводится к уравнению