
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел I. Введение в математический анализ.Содержание книги
Поиск на нашем сайте
Тема 1.1.. Основы теории множеств. Понятие функции. Литература: Шипачев В.С. Сборник задач по высшей математике. Глава 4. Практика 1,2. Функция. Графики элементарных функций. Преобразования графиков. На занятии: № 17,19,29,39,83, 89, 113, 131, 135, 143, 159, 183, 189, 193. Дома: № 18,22,42,86, 98, 104, 114, 126, 132, 142, 174. Практика 3. Элементы математической логики. На занятии: Задание 1. На вопрос, кто из трех студентов изучал логику, был получен правильный ответ: если изучал первый, то изучал и третий, но не верно, что если изучал второй, то изучал и третий. Кто изучал логику? Задание 2. Определить, кто из четырех студентов сдал экзамен, если известно, что: 1) если первый сдал, то и второй сдал; 2) если второй сдал, то третий сдал или первый не сдал; 3) если четвертый не сдал, то первый сдал, а третий не сдал; 4) если четвертый сдал, то и первый сдал. Задание 3. Составить таблицу истинности для высказываний:
Задание 4. В следующих предложениях вместо «…» вставить одно из следующих, подходящих по смыслу выражений: «необходимо», «достаточно», «необходимо и достаточно». А. Для того, чтобы целое число делилось без остатка на 2 «…», чтобы последняя цифра была 8. В. Для того, чтобы уравнение С. Для того, чтобы неравенство D. Для того, чтобы целое число делилось без остатка на 10 «…», чтобы последняя цифра была 0. Задание 5. На языкелогических символов записать определение функции, убывающей на интервале (а; b). Составить отрицание данного утверждения. Дома: Задание 1. Виктор, Роман, Юрий, Сергей заняли на математической олимпиаде первые четыре места. Когда их спросили о распределении мест, они дали три таких ответа: 1) Сергей- первый, Роман- второй; 2) Сергей- второй, Виктор- третий; 3) Юрий- второй, Виктор- четвертый. Как распределились места, если в каждом ответе только одно утверждение истинно? Задание 2. Составить таблицу истинности для высказываний:
Задание 3. В следующих предложениях вместо «…» вставить одно из следующих, подходящих по смыслу выражений: «необходимо», «достаточно», «необходимо и достаточно». А. Для того, чтобы уравнение Б. Для того, чтобы уравнение В (дополнительный). Для того, чтобы дифференцируемая функция Задание 5. На языкелогических символов дать определение периодической функции. Составить отрицание данного утверждения.
Раздел II. Теория пределов. Непрерывность
Тема 2.1. Предел последовательности. Литература: Шипачев В.С. Сборник задач по высшей математике. Глава 2. Практика 4. Вычисление предела последовательности. На занятии: № 21-39 (не четные), 63-71 (не четные). Дома: № 22-40 (четные), 64-72 (четные). Тема 2.2 Предел функции. Литература: Шипачев В.С. Сборник задач по высшей математике. Глава 4. Практика 5,6,7. Вычисление предела функции. На занятии: 235-275 (не четные), вычислить пределы 1) Дома: 234-280 (четные). Тема 2.3 Бесконечно малые и бесконечно большие величины. Литература: Шипачев В.С. Сборник задач по высшей математике. Глава 4. Практика 8. Сравнение бесконечно малых. На занятии: 307-317 (не четные) Дома: № 308-314 (четные). Практика 9. Вычисление пределов при помощи замены бесконечно малых эквивалентными. На занятии: 329-345 (не четные) Дома: № 330-346 (четные).
Тема 2.4. Непрерывность функции. Классификация точек разрыва. Практика 10. Классификация точек разрыва.
Раздел III. Дифференциальное исчисление функции одного переменного Литература: Шипачев В.С. Сборник задач по высшей математике. Глава 5. Тема 3.1. Производная. Практика 11. Вычисление производной. На занятии № 11-45 (не четные). Дома: 12-40 (четные). Практика 12,13. Производная сложной функции. Производная степенно-показательной функции. На занятии № 49, 53, 59-67 (не четные), 73-81 (не четные), 135, 137. Дома: № 50, 54, 56, 60,64, 68-80 (четные), 136, 138.
Тема 3.2. Дифференциал. Практика 14. Вычисление дифференциала функции. На занятии № 147-159 (не четные) Дома № 146-158 (четные)
|
||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 429; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |



 не имело решений «…», чтобы выполнялось условие
не имело решений «…», чтобы выполнялось условие  .
. где
где  выполнялось для всех
выполнялось для всех  «…» чтобы выполнялось условие
«…» чтобы выполнялось условие 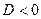 .
.

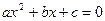 , где
, где  .
. имело хотя бы одно решение «…», чтобы выполнялось условие
имело хотя бы одно решение «…», чтобы выполнялось условие  .
. имела экстремум в точке
имела экстремум в точке  «…», чтобы выполнялось условие
«…», чтобы выполнялось условие  .
. , 2)
, 2) 
 Исследовать на непрерывность и построить графики функций:
2.
Исследовать на непрерывность и построить графики функций:
2.  3.
3.  Найти точки разрыва и исследовать их характер.
4.
Найти точки разрыва и исследовать их характер.
4.  5.
5. 
 Исследовать на непрерывность и построить графики функций:
2.
Исследовать на непрерывность и построить графики функций:
2.  3.
3.  Найти точки разрыва и исследовать их характер.
4.
Найти точки разрыва и исследовать их характер.
4. 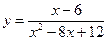 5.
5. 



