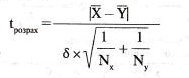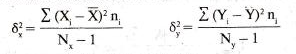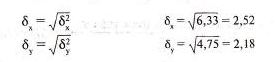Теоретичні знання для методиста.

Традиційно діагностичне обстеження грунтується на ідеї вибіркового методу. Основне розуміння методу зводиться до того, що дослідженню піддягає генеральна сукупність не в повному обсязі, а своєю репрезентативною частиною вибірковою сукупністю. Передбачається, що вибірка з належною вірогідністю представляє генеральну сукупність тільки в тому випадку якщо її елементи обрані з генеральної нетенденціозно.

Щодо обсягу вибірки, то, відповідно до основних положень математичної статистики, вибірка тим репрезентативніша, чим вона повніша. У кожному конкретному випадку кількість об'єктів, що відбираються до вибірки, призначається індивідуально.

Основним завданням вибіркового методу є пошук двох показників

середнього арифметичного значення (X) і середнього квадратич­ний відхилення (δ).

У практиці діагностування прийнято обирати надійність Р = 0,95 відповідний до неї рівень значущості L = 0,05, відображаючи як основну групу досліджуваних завдань. У виняткових випадках за необхідністю різко збільшити надійність обчислювання приймається Р= 0.99 і L = 0.01.

Великий клас завдань вибіркового методу класифікується як клас порівняльних завдань. Порівнюються дві або більше вибіркові сукупності. При порівнянні встановлюється, чи належать ці вибірки і однієї й тієї ж генеральної сукупності або до різних. Це має значен­ня при визначенні вірогідності різниць між двома вибірковими передніми арифметичними.

Отже, при роботі вибірковим методом можна знайти основні середньо-статистичні показники великої групи випробуваних за допомогою вивчення малого числа їхніх представників, а також виявити, чи принципова різниця між декількома однотипними групами об'єктів.

За допомогою вибіркового методу математичної статистики можна оцінити:

1. Ефективність освітнього процесу в конкретному дошкільному навчальному закладі (далі - ДНЗ).

2. Рівень підготовленості однієї дитини чи групи дітей дошкільного віку.

3. Перевагу або ідентичність тієї чи іншої методики навчання мови і розвитку мовлення.

4. Необхідність уведення нового педагогічного чинника в освітній процес дошкільного навчального закладу.

5. Вибірковий метод дозволяє порівнювані:

- показники дитини або групи дітей дошкільного віку однієї вікової категорії до і після серії спеціальних занять для виявлення зрушень у цих показниках;

- показники мовленнєвого розвитку, рівня сформованою мовленнєвих навичок тощо в дітей дошкільного віку і дітей що не відвідують ДНЗ;

- показники сформованості мовленнєвих навичок у дітей дошкільного віку, що навчаються в різних умовах або з різними методиками.

Для визначення вірогідності різниць між вибірковими середніми арифметичними необхідно обробити число обох порівнюваних груп за способом варіаційних рядів, тобто визначиш в обох групах: X - середнє арифметичне значення, δ - середнє квадратичне відхилення m - помилку середнього арифметичного значення.

Критерієм визначення вірогідності різниць с розмір, обумовлений за формулою залежно від того, які вибірки порівнюються в процес дослідження зв'язані або незв'язані.

Критерій вірогідності різниць (критерій Стьюдента - t) порівнкз ється з граничним (табличним) значенням що знаходиться спеціальній таблиці Стьюдента для заданої надійності й обсягу вибірки. Для визначення t_rp за таблицею необхідно знати К (число ступенів свободи), що розраховується за формулою:

- у випадку, якщо рівні обсяги вибірок і нерівні середні квадратичні відхилення N₁ = N₂, δ₁ ≠ δ₂ то

К = 2 х N – 2

- у випадку, якщо нерівні обсяги вибірок і нерівні (або рівні середні квадратичні відхилення N₁≠N₂, δ₁ ≠δ₂ або δ₁ = δ₂ то

 

K=N₁ + N₂ -2

При порівнянні t і t_rp визначається вірогідність різниць між двом вибірковими середніми арифметичними.

Якщо в результаті порівняння І. розрахованого за формулою, постійного t_rp виявиться, що t≥t_rp - різниця між порівнюваним вибірковими середніми арифметичними достовірна (не випадкова), істотна, то це пояснюється впливом певних чинників.

Причини достовірних різниць:

- Краща підготовленість однієї конкретної дитини дошкільно­го віку або всієї вікової групи.

- Одна з досліджуваних методик навчання мови і розвитку мовлення краща, найбільш ефективна.

- Ефективно побудовано освітній процесу ДНЗ.

- Застосування однієї й тієї ж методики в різних умовах - причина в тому, що одні умови краще, ніж інші.

- При введенні в освітній процес ДНЗ певного педагогічного чинника з мстою виявлення ефективності його використання

- причина в ефективності застосування експериментального педагогічного чинника.

Якщо при порівнянні t розрахункового і t постійного вия­виться, що t<t_rp різниця між порівнюваними вибірковими серед­німи арифметичними недостовірна (випадкова), то це пояснюється впливом випадкових чинників.

Причини недостовірних різниць:

- Неправильний добір вибірки.

- Недостатня чисельність вибірки.

- Однаковий рівень підготовленості обох досліджуваних груп або дитини дошкільного віку

- Неефективно побудовано освітній процес в ДНЗ.

- У випадку порівняння двох методик навчання мови і розвитку мовлення - ефект однаковий, методики ідентичні, не має значення, за якою методикою працювати.

- При введенні в освітній процес ДНЗ нового педагогічного чинника з метою виявлення ефективності його застосування

- причина в негативному впливі нового педагогічного чинника на ефективність освітнього пронесу.

- У випадку застосування однієї методики в різних умовах причина - в однаковому результаті навчання в різних умовах, немає істотних різниць, у яких умовах застосовувати досліджувану методику.

Порівняння двох вибіркових середніх арифметичних

Теоретичні знання

При порівнянні двох вибіркових середніх арифметичних звичайно перевіряється припущення, що і перша, і друга вибірки належать до однієї генеральної сукупності і, отже, значною мірою не відрізняються одна від одної (порівнюються за одним показником два спортсмени, дві групи). У такому випадку бувають відомі такі статистична характеристики: X, Y,δ_x, δ_y і обсяги вибірок N₁ i N₂

Дія відповіді на питання щодо достовірності і недостовірності різниць досліджуваних вибірок необхідно порівняти і розрахункове постійний граничний розмір (t_rp).

Вибір формули для визначення критерію достовірності (t) для незв'язаних вибірок залежить від рівності і нерівності обсягів вибірок (N) і середніх квадратичних відхилень (δ):

1. У випадку рівних обсягів вибірок і нерівних дисперсій: N_x = N_y; δ_x ≠ δ_y

 

де X, Y - середнє арифметичне значення першої і другої вибірки;

δ_x²,δ_y² - дисперсія першої і другої вибірки;

N — обсяг вибірки.

Число ступенів свободи для визначення розраховується формулою:

K= 2× N -2

2. У випадку нерівних обсягів вибірок і нерівних дисперсій: N_x ≠ N_y; δ_x ≠ δ_y

Число ступенів свободи розраховується за формулою:

 

К= N_x + N_y - 2

 

2. У випадку нерівних обсягів вибірки і рівних дисперсій:

N_x = N_y; δ_x = δ_y = δ

Число ступенів свободи К= N_x + N_y - 2

Після того, як визначене значення і розраховане, його порівнюють її граничним значенням (t_rp).

Якщо t≥t_rp - різниця між двома вибірковими середніми арифметичними достовірна (не випадкова), а якщо t < t_rp - не дос­товірна (випадкова).

Приклад: В 2-х групах дітей середнього дошкільного віку X_i і Y_i обмірювана різниця ЧСС, уд./хв

Обмірювана ЧСС після виконання 10 присідань. Установити, чи достовірні різниці за показником ЧСС у дослі­джуваних групах дітей середнього дошкільного віку і чому:

Хід роботи:

1. Визначаємо середнє арифметичне значення 2-х вибірок:

2. Визначаємо диспресії 2-х вибірок:

 

 

Для подальшої роботи будуємо таблиці:

а) Для показників першої вибірки.

 

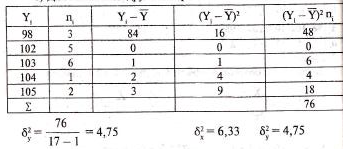
б) Для показників другої вибірки.

3. Визначаємо середнє квадратичне відхилення 2-х вибірок:

4. Визначаємо t_{розрахункове}:

t=

 

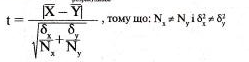
5. Визначаємо число ступенів свободи (К)

 

6. Порівнюємо t_{розрахункове} і t_{граничне}:

t>t_rp (7,59>2,03) – різниці між двома досліджуваними групами плавців достовірна (не випадкова)

Висновок:

t>t_rp (7,59>2,03) – різниці між двома групами дітей середнього дошкільного віку за показником ЧСС достовірні (не випадкові) і пояснюються кращим рівнем підготовленості дітей середнього дошкільного віку першої групи, тому що X<Y(96<102)