
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Паспортний вік дитини дошкільного віку — 3 роки, і вік у день діагностичного обстеження — 3 роки 5 місяців.Содержание книги
Поиск на нашем сайте
Необхідно запропонувати завдання для діагностичного обстеження дітей 3 років і 6 місяців. Таблиця 2 Дні року в десятичній системі
Теоретичні знання для методиста. Сучасні наукові дослідження містять великі масиви вимірів. Такі обсяги чисел важко піддаються аналізу, тому в практиці роботі методиста дошкільного навчального закладу не потрібні. Проте спеціальні статистичні операції дають можливість скоп центрувати початковий кількісний матеріал, не втрачаючи корисні інформації. З погляду математичної процедури, такого роду робота зводиться до формування деяких математичних систем, основні характеристик яких дають поняття про початковий масив чисел.
Робота над методом середніх величин ґрунтується на трьох основних етапах: . Утворення варіаційного ряду. 2. Знаходження основних характеристик варіаційного ряду: - обсяг вибірки (N); - середнє арифметичне значення (X); - медіана (МеХ): - мода (МоХ); - дисперсія (δ 2); - середнє квадратичне відхиленая (δ); - похибка середньою арифметичного значення (m); - коефіцієнт варіації (V). 3. Практична реалізація отриманих характеристик. Практична реалізація отриманих характеристик Метод середніх величин дає можливість визначити середнє значення, припустимі границі (межі) досліджуваної вибірки і визначиш правильність добору досліджуваної групи дітей, її однорідність і однотипність. Тільки правильно дібрана група, однорідна й одної інша, може брати участь у діагностичному обстеженні. Якщо група правильно дібрана, то результати дослідження можуть бути використані і» подальшій оцінці й аналізі методики навчання, ефективності освітнього процесу. Прикінцевий результат діагностичного обстеження можна буде вважати результатом проведеної освітньої робото в конкретному дошкільному навчальному закладі, а не наслідком закономірного розвитку, навчання і виховання. Правильність добору досліджуваної групи. Утворення варіаційного ряду. Для того щоб скласти варіаційний ряд, необхідно виконати роботу за ранжиром. 1. Ранжирування - операція розташування варіант у порядку зростання або убування. 2. Числа, що входять до складу ряду, що ранжуеться, називаються варіантами, варіанта (Х1) - значення ознаки, що спостерігається. 3. Кожна варіанта в ряду, що ранжирується, зустрічається визначену кількість разів - частота варіанти (n1) 4. Частота варіанта число зустрічальності варіанти в ряду, що ранжирується. Знаючи частоту варіанти й обсяг вибірки, можна за допомогою формули розрахувати відсоток зустрічальності
варіанти в рапжируьамому ряді, відносна частота або частотність(Y):
де ni — частота варіанти; N — обсяг вибірки. Вибірка (вибіркова сукупність) - ряд результатів, поданих випадковими числами. Генеральна сукупність — сукупність усіх значень, що можна було одержати дія вибірки, що досліджується. Якщо дослідженням охоплена вся генеральна сукупність, то так дослідження є репрезентативним. Такі дослідження здійснюються досить рідко. Так, якщо досліднику вдалося обстежити рівень сформованою звукової культури мовлення у всіх дітей старшого дошкільного віку, що мешкають на теренах України, тобто провести репрезентативне дослідження, то виходить, що обстежена вся генеральна сукупність Усі подальші дослідження будуть вважатися вибірковими (дослідження на рівні області, наприклад). Або рівень сформованості граматично правильного мовлення (як що нас цікавлять результат за досліджуваними показниками дітей тільки одного ДНЗ) - вибіркова сукупність, а рівень сформованою граматично правильного мовлення в дітей усіх дошкільних навчальних закладів України - генеральна сукупність. 5. Обсяг вибірки (N) - одна з основних характеристик варіацій ного ряду, що визначається числом об'єктів спостереження або загальної кількості варіант, у ранжируваному ряді, що спостерігається. 6. Варіаційний ряд - ранжируваний ряд із указівкою частоти або відносної частотності. 7. Накопичена частота (k) визначається як підсумовування попередніх частот. Накопичена частота першої варіант в ранжируваном ряді дорівнює її ж частоті, а останньої варіанти - загальні кількості варіа нт досліджуваного ранжируваного ряду. 8. Медіана (МеХ) - основна характеристика варіаційного ряду визначається як середня варіанта, що поділяє ранжируваний ряд навпіл. Залежно від парності або непарності вибірки медіана розраховується за формулою: якщо обсяг вибірки непарний:
якщо обсяг вибірки парний:
9. Мода МеХ) - основна характеристика варіаційного ряду і визначається як варіанта з найбільшою частотністю. Якщо дві варіанта ранжируваного ряду мають однакову найбільшу частоту і розташовуються поруч, то мода — середні арифметичне значення цих двох варіант, якщо розташовані в різних місцях ранжируваного ряду, то існують дві моди і вибірка, що називається біомодальною; якщо всі варіанти зустрічаються однакову кількість разів - моди не. існує. 10. Середнє арифметичне значення (X) - основна характеристика варіаційного ряду, що визначається як середній результат вибірки, що досліджується. Середнє арифметичне значення розраховується за формулою:
якщо всі варіант» зустрічаються по одному разу (n=1) - це не зважене середнє арифметичне значення. X1,Х2 - варіанти ранжируваного ряду;
Хn - остання варіанта досліджуваного ранжируваного ряду. Зважене середнє арифметичне значення, якщо не всі пв1; ∑- знак підсумовування. 11. Графік залежності варіанти від частото дає уявлення про нормальний закон розподілу Нормальний закон розподілу закон, за яким переважна більшість варіант зосереджена в центрі, а в міру віддалення від центру кількість їх поступово зменшується, зберігаючи абсолютну асиметрію лівого правого крила нормальної кривої. Якщо результати вимірів за своїми характеристиками можуть бути віднесеш до нормального розподілу, то вибір статистичного метод для аналізу результатів визначений. Це дуже важливо, оскільки для діагностичного обстеження дітей зменшується ступінь ризик; використання неправильного статистичного методу аналізу. На графіку залежності варіанта від частоти показано: · якщо медіана, мода і середнє арифметичне значення знаходяться в одній крапці - нормальний розподіл (малюнок 1); · якщо медіана і мода ліворуч від середнього арифметичног о значення - лівостороння асиметрія (малюнок 2) · якщо праворуч - правостороння асиметрія (малюнок 3)
На основі порівняння медіани, моди, середнього арифметичного значення і побудови графіка залежності варіанти від частотності можливо зробити висновок про правильний добір досліджуваної групи: 1. Якщо значення медіани, моди і середнього арифметичного значення збігаються або незначно відрізняються і графік залежності варіанти від частоти має форму купола, то це дозволяє говорити про нормальний закон розподілу, а досліджувану групу можна вважати правильно дібраною відповідно до віку, статі, рівня мовленнєвого розвитку, і така група може браги участь у подальшому обстеженні. Результати обстеження, отримані за умов правильного добору групи, можна буде використовувати в подальшій роботі, під час порівняння Інших вибірок дітей ДНЗ. 2. Якщо значення медіани, моди і середнього арифметичного значно відрізняються, а графік залежності варіанта від частоти не має форми купола і має місце лівостороння або правостороння асиметрія (не нормальний закон розподілу), то група неправильно дібрана і не може брати участь у подальшому діагностичному обстеженні, отже, необхідно переглянути склад цієї групи, Унаочнимо за допомогою прикладу наведені теоретичні положення. 1. Результати 11 дітей середнього дошкільного віку в називанні предметів прямокутної форми виявилися рівними, а саме: Миколка - 11 слів; Даринка - 15; Максимко - 14і т.д. Тобто ряд має такий вигляд: 10; 15; 14; 11; 11; 12; 13; 12; 9; 13; 12. 2. Кожний із результатів, показаних 11 дітьми, є варіанта - і 10, і 15, і 14... 3. Ранжируваний ряд записуємо в порядку зростання: 9; 10; 11; 11; 12; 12; 12; 13; 13; 14; 15. 4. Обсяг вибірки N = 11. 5. Частота (ni): п, (9) = 1, ni (10) = 1, ni (11) = 2, п, (12) = 3, ni (13) = 2, ni(14)= 1, ni (15)=1. 6. Відносна частота (У):
7. Варіаційний ряд: 7.1. З частотою (ni):
асир
7.2. З відносною частотою:
8. Накопичена частота (К):
9. Медіана (МеХ) У зв’язку з тим що наша вибірка непарна (11 дітей середнього віку), медіану розраховуємо за формулою
X6 – порядковий номер (6) варіанти в ранжируваному ряді; Х6 = 12 10. Мода (МеХ). МоХ =12, тому,що варіанта 12 зустрічається частіше за все, 3 рази (ni (12)=13). 11. Середнє арифметичне значення (Х) Розраховуємо Х за формулою зваженого середнього арифметичного значення;
У середньому кожний із 11 дошкільників назвав 12 предметів прямокутної форми.
12. Графік залежності варіанти (Хі) від частоти (ni).
Розподіл за цим графіком відповідає нормальному закону розподілу куполоподібний графік, значення X, МеХ і МоХ збігаються; переважне нагромадження варіант зосереджено в центрі, в міру віддалення від центру кількість їх поступово зменшується» зберігаючи абсолютну симетрію лівого і правого крила нормальної кривої. Примітка для методиста: у процесі побудови графіка необхідно правильно розрахувати масштаб. Він може бути свій як за віссю абсцис, пік і та віссю ординат. Пік, 11 дітей дошкільного віку, які виконували завдання, мають такі показники:
Для абсцис - якщо ми хочемо розмістити 15 (у нас цс максимальне значення) на 15 см, то кожне виконане завдання відзначається як 1 см, а якщо на 30 см, то 1 р. - 2 см, 2 р. - 4 см... Для ординат — якщо ми хочемо розмістити 3 на 6 см, то кожна одиниця - 2 см. За ординатою 1 - 2 см. за абсцисою 1 - 1 см. Висновок: Група з одинадцятьох дітей середнього дошкільного піку, які виконували завдання, дібрана правильно з урахуванням статі, віку і іншім мовленнєвого розвитку, тому що x значення МеХ і МоХ (мода) рівні» побудова графіка залежності варіанти від частоти відповідає нормальному закону розподілу. Група може брата участь у подальшому обстеженні.
Теоретичні знання для методиста. 1. Однорідність і однотипність групи визначається за коефіцієнтної варіації (V), що розраховується за формулою:
де δ - середні: квадратичне відхилення; X - середнє арифметичне значення. Оцінка однорідності й однотипності проводиться за коефіцієнтної варіації: - якщо V≤10%, то коливання результатів дослідження невелике, групу можна вважати однорідною й однотипною з своїм складом, що може брати участь у подальшому обстеженні - якщо V приймає значення від 10 до 20%, то коливання результатів середнє, склад такої групи необхідно переглянути; - якщо V > 20%, то коливання результатів велике і така група не може брати участь у подальших дослідженнях. 2. Середнє квадратичне відхилення (δ) - основна характеристик варіаційного ряду, що показує відхилення від середнього арифметичного значення, і чим воно менше, тим група більш однорідна й однотипна За можна визначити перевагу тієї або іншої методики навчання сформованості навичок тощо. За допомогою середнього квадратного відхилення можна записати припустимі межі для досліджуване вибірки (Х±δ).
3. Дисперсія показує розсіювання результатів і визначається за формулою:
де Хi - варіанта, X - середнє арифметичне значення, ni - частота варіанта, N — обсяг вибірки. 4. Похибка середнього арифметичного значення (m) або випадкова похибка вимірів виникає з причин, які можна передбачити, але не можна заздалегідь усунути (стан здоров'я дитини, її настрій тощо). Залежно від обсягу вибірки похибка середнього арифметичного значення може бути розрахована за формулою:
де N — обсяг вибірки. Розглянемо пропонований теоретичний матеріал на прикладі. Наприклад: Одинадцять дітей дошкільного віку під час обстеження рівня сформованості фонематичного слуху показали результати: 910 12 14 1511 11 1212 13 13 Визначаємо, наскільки група однорідна й однотонна і чи може вона брати участь у подальших дослідженнях? 1. Ранжируваний ряд: 9 10 11 11 12 12 1213 13 14 15 2. Варіаційний ряд із указівкою частоти.
3. Середнє арифметичне значення (Х) Через те що середнє арифметичне значення зважене, застосовуємо формулу:
X=12 – середній результат рівня сформованості фонематичного слуху для 11дітей дошкільного віку(у середньому кожний із 11 дітей дошкільного віку виконав 12 завдань). 4. Дисперсія (δ2):
4.1. Креслимо таблицю розрахунку δ2:
4.2. Розраховуємо δ2 за формулою:
δ2= 30: (11-1)= 30:10=3
5. Середнє квадратичне відхилення (δ):
6. Припустимі границі для нашої вибірки (Х + δ) 12 + 1,73→10,27 – 13,73 – у дані границі входить 7 результатів із 11.
7. Коефіцієнт варіації (V)
8. Похибка середнього арифметичного значення (m). У нашому випадку похибка середнього арифметичною значення розраховується за формулою:
Висновок: коефіцієнт варіації 14,4% - середнє коливання результатів. Група дітей дошкільного віку може брати участь у подальшому діагностичному обстеженні, а якщо буде можливість - краще переглянути склад групи.
Теоретичні знання для методиста. Під час діагностичних обстежень дітей дошкільного віку між показниками, що досліджуються, часто спостерігається взаємозв'язок. Види взаємозв'язку можуть бути різними. Розрізнюють два види взаємозв'язку: функціональний і статистичний. Функціональний взаємозв'язок - це залежність, коли кожному значенню одною показника відповідає строго визначене значення іншого і ніякої варіації бути не може. До другого виду взаємозв'язку відносять, наприклад, залежність рівня сформованості навичок від методу навчання. Одному значенню сформованості навички може відповідати декілька застосованих методів і навпаки. У таких випадках, коли одному значенню одною показника відповідає декілька значень іншого показника, взаємозв'язок називається статистичним. Вивченню статистичного взаємозв'язку між різними показниками приділяють велику увагу, тому що це дозволяє розкрити деякі закономірності і надані описати їх як словесно, так і математично і метою застосування в практичній роботі методиста дошкільного навчального закладу. Серед статистичних взаємозв'язків найбільш важливі - кореляційні (від лат. correlatio - співвідношення, відповідність). Кореляція - вид взаємозв'язку між ознаками. Кожна ознака великою кількісно однотипних показників, що варіюють. Кореляція полягає в тому, що середній розмір одного показника змінюється залежно від середнього розміру іншого. Статистичний метод, що застосовується для дослідження взаємозв'язків, називається кореляційним аналізом. Головне завдання кореляційного аналізу - визначення форми, тісноті спрямованості досліджуваних показників. Він широко застосовуєш: в теорії тестів для оцінки їхньої надійності й інформативності. За допомогою кореляційного аналізу можна оціниш: - Взаємозв'язок між результатами навченості і функціональним показниками (кількість правильних відповідей під час обстеження і групою здоров'я дитини); - Вплив навчально-мовленнєвої діяльності на результат (результат діагностики рівнів сформованості фонематичного слуху, словникового запасу, граматичної правильності мовлення і результат який одержано під час аналізу кількісного складу лексики); - Взаємний вплив показників навченості дитини (результат діагностування сформованості мовленнєвих навичок і рівня сформованості фонематичного слуху); - Надійність тесту (погодженість, стабільність); 4.1. Погодженість - оцінка рівня сформованості граматичних навичок з боку двох педагогів (вихователь і методист; вихователь і психолог тощо); 4.2. Стабільність порівняння результатів тесту (кількість правильних відповідей із десятьох запропонованих) і ретесту - те ж завдання, але через рік; - Інформативність тесту (залежність між кількістю правильні відповідей за 60 секунд і часом виконання повного комплекс завдань) тощо. Аналіз взаємозв'язку починається з графічного уявлення результатів вимірів у прямокутній системі координат. Графічна залежність має назву діаграма розсіювання, або кореляційне поле. Візуальні аналіз кореляційного поля дозволяє виявити спрямованість і форм залежності (принаймні, зробити припущення). За кореляційним полем можна визначити спрямованість: а) пряма позитивна кореляційна статистична залежність (нахил кореляційного поля вправо): - зі зростанням (зменшенням) першої ознаки (Xі) інша (Yi) також зростає (зменшується); - зі зростанням першої ознаки (Xi) інша (Yi) зменшується; і навпаки, - зі зменшенням першої ознаки (Xi) інша (Yi) зростає; б) зворотна негативна кореляційна статистична залежність (нахил кореляційного поля вліво). Якщо кореляційне поле подане окружністю, то залежність відсутня.
Форми статистичної залежності: 1. Лінійна форма залежності — форма близька до звичайної геометричної фігури - еліпса. 2. Нелінійна форма залежності - будь-яка інша форма, крім еліпса. Якщо кореляційне поле подане прямою лінією, то має місце функціональна залежність.
Отже. візуальний аналіз кореляційного поля дозволяє виявити форму статистичної залежності - лінійну або нелінійну. Це мас істотне значення для наступного кроку в аналізі - вибору й обчислення відповідного коефіцієнта кореляції. Для більш точної оцінки кореляції, що визначається за формулою потрібно знати форму залежності: Якщо виміри проводяться за шкалою відношень або інтервалів і форма залежності лінійна, то коефіцієнт кореляції розраховується формулою Браве-Пірсона (rxy):
Xi й Yi - варіанти 2-х вибірок; X і Y- середнє арифметичне значення показників Xi , Yi; δx, δy - середнє квадратичне відхилення; N - число вимірів (випробуваних). 2. Якщо виміри проводяться за шкалою відношень або інтервалів форма залежності нелінійна, коефіцієнт кореляції (rxy) розраховуєш за формулою:
Для оцінки тісноти взаємозв'язку в кореляційному аналізі застосовується значення спеціального показника коефіцієнт кореляції (rxy). Абсолютне значення коефіцієнта кореляції знаходиться в межах від 0 до 1 - пряма поштивна кореляційна статистична залежність і від до 0 - поротна негативна кореляційна статистична залежність:
-1≤ rxy ≤ 1
Пояснюють значення цього коефіцієнта у такий спосіб: а) rxy = 1 зв'язок між ознаками дуже тісний (функціональний взаємозв'язок); б) rxy = 0 зв'язок між ознаками Xі й Vі відсутній; в) чим ближче до нуля, тим зв'язок слабкіший, чим ближче до одиниці - тим тісніший. Прийнято вважати, що rxy= 0,2....0,49 - слабкий зв'язок; rxy =0,5....0,69 - середній зв'язок; rxy=0,7....0,99 - тісний (сильний) зв'язок. На кореляційному полі тіснота може виглядати так: а) якщо крапки групуються вздовж якої-небудь лінії, то зв'язок є і він тим тісніше, чим ближче вони групуються.
rxy=0,89 сильна кореляційна статистична залежність; б) якщо крапки розсіяні хаотично, зв'язок між ознаками відсутній або дуже слабкий; rxy = 0.09 - дуже слабка кореляційна статистична залежність. Проте варто пам'ятати, що при роботі з великою точністю, наприклад при оцінці кореляцій з високим рівнем мовленнєвого розвитку дітей дошкільного віку, коефіцієнт кореляції відображає тісний зв'язок, якщо він не менше 0,9. У деяких випадках тісноту взаємозв'язку визначають на основі коефіцієнта детермінації (D), що розраховують за формулою:
Цей коефіцієнт визначає частину загальної варіації одного показника, що пояснюється варіацією іншого показника. Залишок відсотків варіації від ста пояснюється впливом інших, не врахованих чинників. Розглянемо пропонований теоретичний матеріал на прикладі. Наприклад: Чи існує залежність і яка між результатами бігу дітей старшого дошкільного віку на 60 м (Xі),сек. і швидкістю їзди на велосипеді (Yi), км/год. у 7 велосипедистів? Чи може біг на 60 м служити тестом для дітей-велосипедистів на виявлення швидкості їзди на велосипеді? Наскільки сильно вплив біг на 60 м на швидкість їзди на велосипеді?
Рішення: Розрахунок середнього арифметичного значення 2-х вибірок Хі і Yi 1.1. Якщо всі варіанти першої вибірки (Xі) мають частоту одиниці то середнє арифметичне значення розраховуємо за формуло зваженого середнього арифметичного значення:
X = 9,3 (сек.) - середній час пробігання дистанції 60 м для велосипедистів. 1.2. Зворотний кореляційний статистичний взаємозв'язок - нахил то середнє арифметичне значення розраховуємо за формулою, незваженого середнього арифметичного значення:
Y= 17,4 (км/год) – середня швидкість їзди на велосипеді для 7 велосипедистів. Рішення: 2. Побудова кореляційного поля, за яким визначаємо форму і спрямованість взаємозв’язку:
Побудова кореляційного поля відповідає нелінійній формі залежності і зворотному кореляційному статистичному взаємозв'язку. Нелінійна форма залежності кореляційне поле, подане не у формі еліпса. Зворотний кореляційний статистичний взаємозв'язок - нахил кореляційного поля вліво. Рішення: 3. Якщо форма залежності нелінійна, то коефіцієнт Кореляції озраховується за формулою:
3.1. Для подальшої роботи будуємо таблицю:
3.3. Коефіцієнт кореляції (rxy):
rxy = -0,96 значення коефіцієнта дозволяє говорити негативний сильний кореляційний статистичний взаємозв'язок. 4. Розрахунок коефіцієнта детермінації (D):
D = 92,16 значення коефіцієнта дозволяє говорити про тe що, 92% взаємозв'язку результату з бігу на 60 у і їзди на велосипед пояснюється їхнім взаємовпливом. Інша частина (100% - 92% = 8%) варіації пояснюється впливом інших неврахованих чинників. Висновок: Знайдений коефіцієнт кореляції (rxy=0,96) указує на зворотний негативний сильний кореляційний статистичний взаємозв'язок між бігом на 60 м і їздою на велосипеді. Це означає що зі зменшенням часу проходження дистанції 60 м швидкість їзди на велосипеді буде зростати. Коефіцієнт детермінації дозволяє стверджувати, що на 92% (із 100%) швидкість їзди на велосипед залежить від часу бігу на 60 м Отже, біг на 60 м доцільно застосовувати на етапі підготовки для дітей-велосипедистів, на виявлення швидкості їзди на велосипеді.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 282; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.176.191 (0.014 с.) |






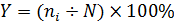





 , тому що не всі варіанти мають ni =1:
, тому що не всі варіанти мають ni =1:

 де δ2 - диспресія
де δ2 - диспресія

 , якщо N>20; або
, якщо N>20; або  , якщо
, якщо  ,
,

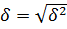


 у що N < 20(N=11)
у що N < 20(N=11)











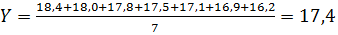 (км/год)
(км/год)







