
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розподіл ефективності за ПаретоСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Точка 1. Не існує способу підвищити добробут всіх учасників обміну, або 2. не існує способу підвищити добробут якогось індивіда не знижуючи добробут когось іншого, або 3. усі вигоди від обміну вичерпані або 4. відсутня можливість здійснення взаємовигідних угод.
З умови дотикання випливає, що в ящику Еджварта існує багато розподілів, ефективних за Парето тому множина всіх точок розподілів, ефективних за Парето в ящику Еджварта називається множиною Парето, або контрактною кривою. Зауваження: контрактна крива завжди проходить через лівий-нижній і верхній-правий кути ящика Еджварта. 86. Оптимальність в обміні. Продуктова «Коробка Еджворта» Ефективність при обміні обумовлена, насамперед, гранич.нормами заміщення, які притаманні учасникам мінових (торгових) операцій. До тих пір, поки ці норми різняться між собою. Існує можливість взаємовигідного обміну й підвищення ефективності. Розподіл товарів є ефективним тоді, коли гранич.норми заміщення між будь-якими парами товарів однакові для всіх споживачів, тобто подальше продовження мінових операцій призведе до зниження ефективності розподілу. Умови ефективності обміну у формалізованому вигляді можна представити таким чином. Два споживачі С і П шляхом взаємообміну міняють кількості придбаних товарів А і В доти, поки співвідношення цін на них не дорівнюватиме їхнім граничюнормам заміщення товару А товаром В: (17.1 ст.169) Якщо розглядати споживання товару В як еквівалент грошових витрат (З) на придбання всіх інших товарів, крім товару А, то можна сформулювати такі умови еф-ті: (17.2 ст.169). При цьому можна визначити суму грошей (З), яку споживачі С і П можуть залучити для додаткової кількості товару А. Значення грани.нора заміщення хар-зує певну суму грошей, призначену для придбання інших товарів, яку потрібно спрямувати для додатк.одиниці товару А. Аналогічні підходи, як і при обміні, але тут вивчаються, відповідно, гранич.норми техніч.зам-ня. Для дослідж.еф-ті як обміну, так і вир-ва може бути застосована діаграма Еджворта (модель, що дозволяє унаочнити зміни розміщення обмежених ресурсів між двома товарами (при виробництві) ябо між двома благами (при споживанні) і досягнення ефективного розподілу цих ресурсів). При побудові діаграми відбувається накладання двох карт ізоквант (кривих байдужості), початки координат яких розташовані один проти одного, в рез-ті чого створюється замкнутий простір, що має назву коробки Еджворта. На рис.17.2 ст.169 за доп.діаграми Еджворта розглядаються варіанти розподілу ресурсів (капітал і праця) для вир-ва двох товарів А і В.
Лише ті комбінації факторів вир-ва, які відповідають умовам дотику двох ізоквант у коробці Еджворта, означають варіанти еф-го розподілу ресурсів. Це досягається в разі рівності кутів нахилу ізоквант, тому формальною ознакою еф.розподілу виробн.факторів є рівність гранич.норм техніч.зам-ня: 17.3 ст.170. Таких варіантів може бути безліч. Якщо об”єднати певну кіль-ть точок, кожна з яких відповідає тхнічно еф-ним варіантам використання ресурсів, то отримаємо криву виробничих контрактів (крива контрактів (виробничих контрактів) – чисельність можливих ефективних варіантів розподілу двох ек.благ між двома споживачами (двох виробничих ресурсів між двома товарами), для яких виконуються умови: ст.172). Еф-ть вир-ва досягається тоді, коли вже неможливо перерозподілити ресурси для того, щоб збільшити випуск одного товару, буз зменшення вир-ва іншого. Крива виробничих можливостей – лінія, що показує усі максимально можливі комбінації виробництва двох товарів за фіксованого використання ресурсів та даного рівня розвитку технології (рис.17.3 ст.170). Кожна точка дотику ізоквант двох товарів у коробці Еджворта відпоівідає точці на кривій виробн.можливостей. При русі вздовж цієї кривої Змінюються пропорції заг.вир-ва, і ці зміни дає зиогу аналізувати гранич.норма трансформації товару А в товар В. Вона показує від якої кільксті товару А слід відмовитися для збільшення випуску товару В на одну одиницю: (17.4 ст.170) Вир-во тоді буде нф-ним, якщо воно буде максимізувати корисність для споживачів і водночас не виходитиме за межі наявних ресурсів, тобто знаходитиметься на кривій можливостей. Отже, межа виробничих можливостей та крива байдужості, що відображає макс.рівень задоволення потреб, будуть мати тільки одну заг.точку – точку дотику (рис.17.4 ст.170).
Ящик Еджварта Нехай в економіці діють 2 особи (А і В) і 2 товари: Розподіл називається практично здійсненним, якщо практичне споживання кожного товару дорівнює загальній наявній кількості цього товару. Нехай Практично здійсненний набір: 87.Оптимальність у виробництві та ефективність використання ресурсів. Умови ефективності у виробництві розглянемо для економіки,де відомі фіксовані обсяги ресурсів,що використовуються у виробництві благ. У такій системі треба прийняти рішення про розподіл ресурсів між різними галузями,кожна з яких випускає одне благо і, визначити оптимальні обсяги виробництва благ.
Графічно всі можливі варіанти розподілу двох обмежених ресурсів між двома фірмами можна показати на діагра.мі (ящику) Еджворта для виробництва (мал. 13.4), на якій суміщаються дві системи координат - одна для виробника блага Х (початок системи координат у нижньому лівому кутку - точка Ох), інша для виробника блага У (початок системи координат у правому верхньому кутку - точка Оу). Довжина і висота ящика визначаються сукупними запасами ресурсів, згідно з умовою (13.5). Будь-яка точка на діаграмі буде мати чотири координати і відбиватиме варіант розподілу ресурсів між двома фірмами; наприклад, точці А на мал. 13.4 відповідає розподіл ресурсів між першою фірмою – (Lx)A, (Kx)A і другою –(Ly)A,(Ky)A. Для кожної з фірм можна побудувати ізокванти, які відповідають певним обсягам випуску: для першої – Х1, Х2, Х3,Х4, для другої – У4, У3, У2, У1 (мал. 13.5); тут обсяги Х та У перераховані в послідовності зростання випуску. Початковий розподіл ресурсів у точці А дає змогу фірмам забезпечити обсяги випуску Х1 та У3. Якщо порівняти стан А зі станом Р1 (який досягається внаслідок певного перерозподілу ресурсів), то перша фірма не скорочує свій випуск Х1, а друга збільшує випуск з У3 до У1. При іншому варіанті перерозподілу, що приводить до стану РЗ' навпаки, друга фірма не змінює випуск, а перша підвищує свій з Х1 до Х3. Можливі також варіанти перерозподілу, коли обидві фірми збільшують свій випуск, наприклад, до рівнів Х2 та У2 (стан Р2). Отже, всі варіанти перерозподілу ресурсів, які відповідають точкам заштрихованого сектора АР1F3(окрім точки F), означають покращення за Паретo. Кожна окрема фірма використовує ефективну (оптимальну) комбінацію ресурсів, що мінімізує вартість виробництва, якщо виконується умова: MPl/MPk=MRTSlk=Pl/Pk. (13.6) Але ринкові ціни факторів Pl, РК для кожної ситуації на ринку однакові для всіх фірм. Отже, якщо кожний виробник досягає ефективності у виробництві, то для граничних норм технологічного заміщення, MRTSx і MRTSy, у виробництві, відповідно, благ Х та У має виконуватись співвідношення (MRTSLK)X=PL /РК =(MRTSLK)y (13.7)
Це і є умовою ефективності (оптимальності за Парето) у виробництві, тому що при виконанні співвідношення (13.7) покращення за Парето за наявних запасів ресурсів неможливе. На мал. 13.5 показано точку Р4, яка відповідає умові (13.7): в цій точці нахили ізоквант Х4 та У4 співпадають з нахилом РL/Рк спільної дотичної до цих двох ізоквант.
|
|||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 448; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.119.149 (0.009 с.) |

 являє собою розподіл ефективний за Парето. Існують такі тлумачення оптимальності за Парето:
являє собою розподіл ефективний за Парето. Існують такі тлумачення оптимальності за Парето: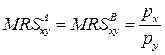 - умова ефективності в обміні.
- умова ефективності в обміні. ,
,  . Пара споживацьких наборів
. Пара споживацьких наборів  називається розподілом.
називається розподілом. - початкові точки, в яких знаходились індивіди А і В до початку розподілу.
- початкові точки, в яких знаходились індивіди А і В до початку розподілу.

 Ефективність(оптимальність за Парето) у виробництві досягається при такому розподілі ресурсів між галузями,що неможливий їх пере розподіл, який збільшував би виробництво будь-якого блага без зменшення виробництва хоча б одного з інших благ. Для геометричної інтерпретації проблеми розподілу ресурсів скористаємось графічною моделлю Еджворта для виробництва, яка зовні схожа на відповідну модель для економіки обміну. Нехай для виробництва двох благ, Х та У (кожне з яких випускає одна фірма) використовуються два види ресурсів у фіксованих обсягах – праця(Lо)і капітал(Ко),які розподіляються між двома виробничими процесами (тобто між двома фірмами) так, що виконуються балансові умови: Lх + Ly = L о, К x +Ку=Ко. (13.5)
Ефективність(оптимальність за Парето) у виробництві досягається при такому розподілі ресурсів між галузями,що неможливий їх пере розподіл, який збільшував би виробництво будь-якого блага без зменшення виробництва хоча б одного з інших благ. Для геометричної інтерпретації проблеми розподілу ресурсів скористаємось графічною моделлю Еджворта для виробництва, яка зовні схожа на відповідну модель для економіки обміну. Нехай для виробництва двох благ, Х та У (кожне з яких випускає одна фірма) використовуються два види ресурсів у фіксованих обсягах – праця(Lо)і капітал(Ко),які розподіляються між двома виробничими процесами (тобто між двома фірмами) так, що виконуються балансові умови: Lх + Ly = L о, К x +Ку=Ко. (13.5)


