
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Аппроксимация функций. Метод наименьших квадратовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Цель работы: изучить метод наименьших квадратов, линейную и квадратичную аппроксимации, алгоритм метода, формулы для вычисления, написать программу на языке программирования, реализующую линейную и квадратичную аппроксимации методом наименьших квадратов. Ход решения для линейной аппроксимации: 1. Определить 2. Вычислить 3. Задать любое значение Ход решения для квадратичной аппроксимации: 1. Определить 2. Вычислить 3. Задать любое значение В формулу линейной и квадратичной аппроксимации можно подставить любое значение Замечание. Результаты линейной и квадратичной аппроксимации должны быть приближенно равными. Варианты заданий Вариант 1
Вариант 2
Вариант 3
Вариант 4
Вариант 5
Вариант 6
Вариант 7
Вариант 8
Вариант 9
Вариант 10
Реализация алгоритмов на языке C#. Для реализации алгоритмов линейной и квадратичной аппроксимаций необходимо произвести немного больше вычислений. Для удобства необходимо создать массив данных, представляющий собой набор элементов одного и того же типа объединённых общим именем. Как показано ниже, создадим фиксированный массив для ряда //создание массива int n = 8; double[] x = new double[8] { 15, 12, 9, 6, 3, 0, -3, -6 }; double[] y = new double[8] { 1, 5.5, 11.5, 16.5, 21.75, 27, 32.25, 37.5 }. Для линейной аппроксимации достаточно организовать всего один метод: // функция для линейной аппроксимации Static double fi(double a0, double a1, double x) { Return a0 + a1 * x; } В основной части программы задаются начальные значения переменных, необходимых для реализации алгоритма, вычисляются значения неизвестных с помощью циклов с параметром FOR, и организуется вывод каждого значения Console.WriteLine («\n Линейная аппроксимация: \n»); double s1 = 0, s2 = 0, s3 = 0, s4 = 0; // вычисление s1-s4 for (inti = 0; i<x.Length; i++) { s1 += x[i]; s3 += Math.Pow(x[i], 2); } for (inti = 0; i<y.Length; i++) { s2 += y[i]; s4 += x[i] * y[i]; } // вычисление а0, a1 Double a0 = (s2۰s3 - s1۰s4) / (n۰s3 - Math.Pow(s1, 2)); Double a1 = (n۰s4 - s1۰s2) / (n۰s3 - Math.Pow(s1, 2)); // вывод на экран вычисленных значений Console. WriteLine("s1= {0}, s2= {1}, s3= {2}, s4= {3}", s1, s2, s3, s4); Console. WriteLine("a0= {0}, a1= {1}", a0, a1); // вывод на экран значения функции For (inti = 0; i<x.Length; i++) { Console. WriteLine("x = " + x[i] + "\tf(x) = " + fi(a0, a1, x[i])); } Для квадратичной аппроксимации алгоритм решения задачи строится аналогичным образом. При этом значения for (inti = 0; i<x.Length; i++) { c4 += Math.Pow(x[i], 3); c6 += Math.Pow(x[i], 4); c7 = c7 + (x[i] * x[i] * y[i]); } Поскольку мы решаем задачу согласно методу Крамера, то для вычисления каждой из дельт необходимо описать несколько дополнительных методов. Ниже представлен программный код методов вычисления static double delta(double c1, double c2, double c4, double c6) { return 8 * (c2 * c6 - Math.Pow(c4, 2)) - c1 * (c1 * c6 - c2 * c4) + c2 * * (c1 * c4 - Math.Pow(c2, 2)); } Static double delta1(double c1, double c2, double c3, double c4, double c5, doublec6, double c7) { return (c3۰c2۰c6 + c5۰c4۰c2 + c7۰c1۰c4 - c2۰c2۰c7 – –c4۰c4۰c3 - c6۰c1۰c5); } Далее можно вычислить значения Double A0 = delta1 (c1, c2, c3, c4, c5, c6, c7) / delta (c1, c2, c4, c6); Double A1 = delta2 (c1, c2, c3, c4, c5, c6, c7) / delta (c1, c2, c4, c6); Double A2 = delta3 (c1, c2, c3, c4, c5, c6, c7) / delta (c1, c2, c4, c6). Контрольные вопросы 1. Аппроксимация. Основная задача аппроксимации. Случаи ее применения. 2. Линейная аппроксимация. Квадратичная аппроксимация. 3. Функции, применяющиеся в качестве аппроксимирующих. 4. Преимущества и недостатки аппроксимации. 5. Способы повышения точности аппроксимации. Глава 6. Интерполяция Одним из типов аппроксимации является интерполяция. Если коэффициенты
т.е. функции совпадают в заданных известных точках, то такой способ аппроксимации называется интерполяцией или интерполированием. При этом точки Интерполяционные кривые, которые строятся отдельно для разных частей заданного интервала изменения Если на всем интервале строится одна функция, то это глобальная интерполяция. Многочлен Лагранжа. В случае если не возникает необходимости иметь коэффициенты многочлена, а надо, лишь найти значения функции в промежуточных точках удобно использовать многочлен Лагранжа. Пусть в точках
где В итоге получим формулу Лагранжа. В эту формулу можно подставить любое значение
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 545; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 по выше описанным формулам.
по выше описанным формулам.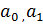 .
. и вывести на экран результаты: аппроксимирующую линейную функцию
и вывести на экран результаты: аппроксимирующую линейную функцию 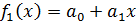 .
.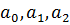 .
.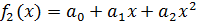 .
.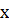 , вычислить значение аппроксимирующей функции и сравнить его с исходными данными.
, вычислить значение аппроксимирующей функции и сравнить его с исходными данными.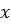

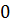
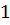

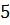
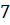

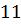
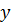
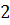
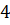
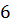
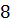
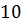
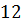


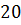

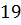
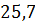



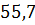
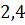
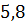
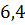
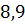


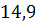
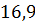
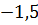
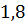
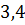

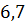
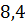
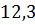
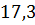
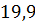



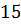
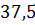
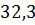
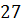


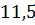
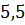
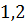

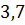
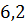
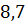

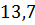
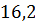
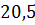
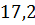
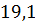
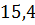




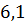
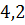
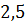
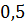
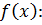
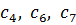 можно вычислить с помощью цикла с параметром:
можно вычислить с помощью цикла с параметром: и
и 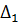 , при этом нахождение остальных дельт осуществляется подобным образом.
, при этом нахождение остальных дельт осуществляется подобным образом.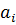 функции
функции 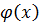 определяются из условия равенства
определяются из условия равенства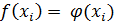 ,
,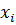 называют узлами интерполяции, а функцию
называют узлами интерполяции, а функцию 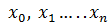 заданы значения функции
заданы значения функции 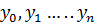 . Необходимо найти значение функции в любой промежуточной точке
. Необходимо найти значение функции в любой промежуточной точке 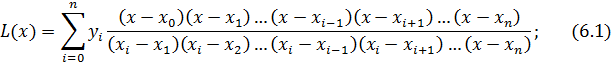
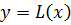 и будет искомым значение функции в точке
и будет искомым значение функции в точке 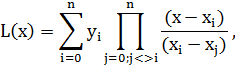
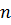 – число точек (пары
– число точек (пары 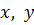 ).
).


