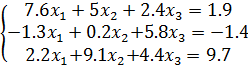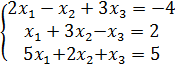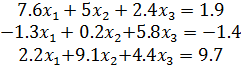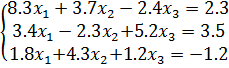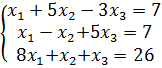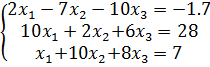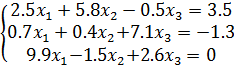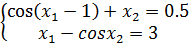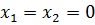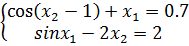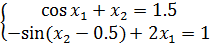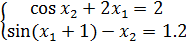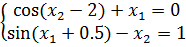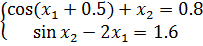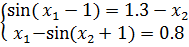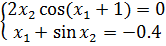Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Этапы нахождения корней уравненияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Глава 1. Общие сведения Математика как наука родилась в ответ на необходимость решения различных практических задач – вычисления каких–либо параметров рассматриваемого процесса. Исследование разнообразных систем или объектов осуществляется с помощью математических методов и математической модели. Математическая модель представляет собой формализованное описание на языке математики исследуемого явления. Таким формализованным описанием может быть система линейных, нелинейных или дифференциальных уравнений, система неравенств, определенный интеграл, полином с неизвестными коэффициентами и т. д. Математическая модель должна передавать важнейшие характеристики исследуемого объекта и отражать связи между ними. Методы решения задачи Для решения задач в математике применяют следующие методы: графические, аналитические, численные. Используя графические методы, в ряде случаев можно оценить порядок искомой величины, например, найти с определенной точностью корни алгебраического уравнения. Графический метод основан на геометрической интерпретации задачи. Аналитические методы позволяют найти решение задачи с помощью формулы или ряда формул. Однако на практике не всегда можно найти решение задачи с использованием аналитических методов. Подобный метод применяется, если для получения результата требуется довольно ограниченное количество вычислений, если известен диапазон, в котором справедливо решение. В качестве примеров аналитических методов можно назвать метод Гаусса, метод Крамера для систем линейных алгебраических уравнений. Численные методы – это основной инструмент решения сложных математических задач. Решение, получаемое численным методом, обычно является приближенным, т.е. содержит некоторую погрешность. Численное решение задачи не может быть выполнено абсолютно точно, поскольку в процессе действий над числами могут возникать и накапливаться ошибки вычислений, связанные с конечной точностью представления чисел в вычислительном устройстве или накапливающиеся в результате выполнения последовательности арифметических операций. К численным методам относятся такие методы, как метод трапеций, прямоугольников, метод простых итераций.
Погрешность вычислений Оценка точности результатов вычислений является важнейшим этапом организации вычисления. Это особенно важно при отсутствии опытных данных для сравнения. Источниками погрешности при использовании численных методов являются: 1.Математическая модель. Погрешность математической модели связана с ее приближенным описанием реального объекта. 2.Исходные данные. Исходные данные, как правило, содержат погрешности, так как они либо неточно измерены, либо являются результатом решения некоторых вспомогательных задач. 3. Метод вычислений. Применяемые для решения задачи методы, как правило, являются приближенными. Например, заменяют интеграл суммой, функцию – многочленом, производную – разностью и т. д. Погрешность метода необходимо определять для конкретного метода. Обычно ее можно оценить и проконтролировать. 4.Округление в вычислениях.Погрешность округления возникает из-за того, что вычисления производятся с конечным числом значащих цифр (для ЭВМ это 10-12 знаков). Округление производят по следующему правилу: если в старшем из отбрасываемых разрядов стоит цифра меньше пяти, то содержимое сохраняемых разрядов не изменяется; в противном случае в младший сохраняемый разряд добавляется единица с тем же знаком, что и у самого числа. Различают абсолютную и относительную погрешности. Абсолютной погрешностью ∆х некоторой величины называют разность между истинным значениемx и приближенным значением х' этой величины:
Относительная погрешность
При сложении и вычитании складываются абсолютные погрешности, а при делении и умножении – относительные погрешности. Критерии численного метода Поскольку погрешность исходных данных и погрешность математической модели считаются неустранимыми и при решении задачи не учитываются, то нам необходимо иметь представление об их влиянии на точность результатов. Решение задачи считается устойчивым по исходным данным, если при малых изменениях исходных данных решение меняется несущественно. Малые погрешности в исходной величине приводят к малым погрешностям в результатах вычислений. Отсутствие устойчивости означает, что даже незначительные погрешности в исходных данных приводят к большим погрешностям или к неверному результату.
Задача считается поставленной корректно, если выполнены следующие три условия: 1. Решение существует при любых допустимых исходных данных. 2. Решение является единственным. 3. Решение устойчиво по исходным данным. Если хотя бы одно из этих условий не выполняется, задача считается некорректной. При анализе вычислительного процесса одним из важнейших критериев является сходимость численного метода, которая обозначает близость полученного решения к истинному:
Другой подход к понятию сходимости используется в методах дискретизации, которые заключаются в замене задачи с непрерывными параметрами на задачу, в которой значения функции вычисляются в фиксированных точках. Это, в частности, относится к численному интегрированию и к решению дифференциальных уравнений. В этом случае под сходимостью метода понимается стремление решения дискретной задачи к решению исходной задачи при стремлении к нулю параметра дискретизации (например, шага интегрирования). Исходя из трех вышеописанных понятий, для получения решения задачи с необходимой точностью ее постановка должна быть корректной, а используемый численный метод должен обладать устойчивостью и сходимостью. Вычислительные методы Под вычислительными методами обычно понимаются методы, которые используются в вычислительной математике для преобразования задач к виду, удобному для реализации на компьютере. Вычислительные методы делятся на прямые (точные) и итерационные. Метод решения задачи называется прямым, если он позволяет получить решение после выполнения конечного числа элементарных операций. В качестве элементарной операции может быть, например, вычисление интеграла, решение системы уравнений, вычисление значений функции и т. д. Важно то, что ее сложность существенно меньше, чем сложность основной задачи. Иногда прямые методы называют точными, имея в виду, что при отсутствии ошибок в исходных данных и при выполнении элементарных операций результат будет точным. Однако, при реализации метода на компьютере неизбежны ошибки округления и, следовательно, наличие вычислительной погрешности. К точным методам относятся метод Гаусса, метод квадратного корня, правило Крамера и т. д. Метод решения задачи называется итерационным, если смысл метода заключается в построении последовательных приближений к решению задачи. Вначале выбирают одно или несколько начальных приближений, а затем последовательно, используя найденные ранее приближения и однотипную процедуру расчета, строят новые приближения. Отдельный шаг итерационного процесса называется итерацией. В результате такого итерационного процесса можно теоретически построить бесконечную последовательность приближений к решению. Поэтому необходимо выбрать критерий окончания итерационного процесса. Критерий окончания связан с требуемой точностью вычислений, а именно: вычисления заканчиваются, когда погрешность приближения не превышает заданной величины. Если последовательность приближений к решению сходится (что бывает не всегда), то говорят, что итерационный метод сходится. К итерационным методам относятся метод простой итерации, метод Зейделя, метод последовательной релаксации.
Решение уравнений Пусть дана некоторая функция
Корень или решение уравнения– значение
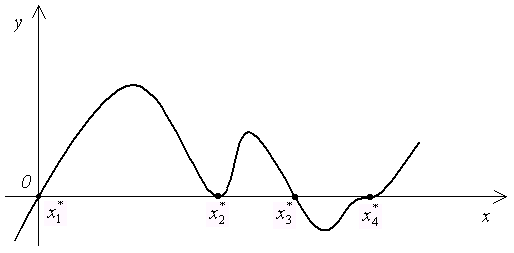
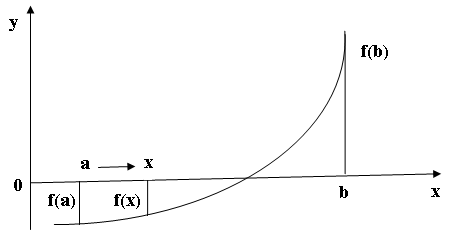
Рис. 1.1. График функции y = ƒ(x)
Корень Геометрически корень уравнения есть точка пересечения графика функции На рис. 1.1. изображен график функции Метод половинного деления Метод половинного деления (дихотомии, бисекции) является самым простым и надежным способом решений нелинейного решения. Метод реализуется следующим алгоритмом. Пусть необходимо решить уравнение Вычислим значение функции в этой точке (рис.2.1) и проверим знак условия Далее продолжаем вышеописанные шаги, т.е. новый отрезок вновь делим пополам и производим новый выбор. Процесс повторяем до тех пор, пока длина отрезка не станет меньше заданной точности
Рис. 2.1. График функции Число итераций при использовании этого метода значительно, и поэтому сходимость его медленная. Однако при любой ширине отрезка Метод простых итераций Метод простых итераций является популярным способом численного решения математических задач. Его суть – нахождение алгоритма поиска по известному приближению (приближенному значению) искомой величины следующего, более точного приближения. Метод реализуется следующим алгоритмом. Пусть уравнение
Выберем на отрезке Продолжая этот процесс неограниченно, получим последовательность приближений к корню:
Процесс итераций сходится при условии Для выбора начального приближения вычисляют значения первых производных функции Геометрически способ простых итераций можно представить следующим образом. Построим графики двух функций:
Рис. 2.2. Графики функций: 2.3. Метод касательных (Ньютона) Метод касательных (Ньютона) является наиболее эффективным методом решения нелинейных уравнений. Метод основан на замене
Рис. 2.3. График функции Уравнение касательной, проходящей через точку
Первое пересечение получим, взяв абсциссу точки пересечения этой касательной с осью OX, т. е.
Аналогично поступаем с остальными точками и в результате получаем последовательность
Метод обеспечивает быструю (квадратичную) сходимость. В качестве первого приближения
Это условие сходимости является достаточным, но необходимым, т.е. если условие выполняется, то итерационный процесс обязательно сойдется, а если не выполняется, то может или сойтись, или не сойтись.
Метод хорд Метод хорд является итерационным численным методом приближённого нахождения корня уравнения. Метод реализуется следующим алгоритмом. Пусть уравнение Рассмотрим геометрическое представление метода (рис. 2.4).
Рис. 2.4. График функции Проведем хорду через точки A и B. В точке пересечения хорды с осью Уравнение прямой, проходящей через две точки
Из этого уравнения необходимо определить точку Один из концов отрезка В качестве подвижного конца выбирается точка, для которой выполняется условие
Уравнение (2.3) можно записать в следующем виде:
Отсюда можно найти искомую точку
Условие сходимости итерационного процесса является достаточным, но не необходимым. Лабораторная работа 1 Алгоритм метода хор д Ввод
Начало цикла
Конец цикла, условие Печать Ход решения: 1. Найти 2. Проверить условие сходимости для корректного ввода начального приближения (подвижной границы) 3. Написать программу, реализующий описанный выше алгоритм, и ввести начальные данные. 4. Вывести на экран результат программы. Замечание. Значение Варианты заданий
Входные данные, после запуска программы – отрезок, содержащий корень (или начальное приближение) и точность вычисления. Выходные данные – найденный корень уравнения и проверка (подстановка найденного значения в исходное уравнение). Метод Крамера Метод Крамера является прямым методом. Это способ решения систем линейных алгебраических уравнений с числом уравнений равным количеству неизвестных с ненулевым главным определителем матрицы, коэффициентов системы. Обычно метод Крамера применяется для систем с очень малым количеством уравнений. Решение представляется в виде
где Система
Метод Гаусса Метод Гаусса принадлежит к группе прямых методов и является классическим методом решения системы линейных алгебраических уравнений. Метод основан на приведении матрицы к треугольному виду. Рассмотрим этот метод на примере системы трех уравнений, а затем распространим его на систему
Умножим первое уравнение на
где
Обобщим эти формулы для системы
где Теперь из третьего уравнения необходимо исключить член, содержащий
где
Теперь матрица системы приведена к треугольному виду, и из третьего уравнения можно найти
Аналогично строится алгоритм для системы с произвольным числом уравнений, который включает два этапа: 1. Прямой ход – приведение матрицы системы к треугольному виду. 2. Обратный ход – вычисление искомых неизвестных. Метод простых итераций Метод простых итераций является одним из простейших итерационных методов. Рассмотрим метод также на примере трех линейных уравнений, а затем применим на систему
Предполагается, что диагональные элементы отличны от нуля, в противном случае надо переставить уравнения. Выразим неизвестные из уравнений
Зададим некоторые начальные (нулевые) приближения:
Обозначим через
Итерации проводятся до тех пор, пока не будет выполнено следующее условие:
Если условие не выполняется, итерации повторяют, приняв
Для сходимости итерационного процесса достаточно, чтобы модули диагональных коэффициентов были не меньше сумм модулей всех остальных коэффициентов:
Это условие является достаточным для сходимости метода итерации, но не является необходимым, т.е. для некоторых систем процесс сходится и при нарушении этого условия. В случае системы линейных уравнений, чтобы получить сходимость и верное решение, необходимо соблюдать условие – на главной диагонали системы должны располагаться максимальные элементы каждой строки (т.е. при необходимости надо переставить строки местами). Метод прогонки Метод прогонки используется для решения систем линейных уравнений с трехдиагональной матрицей:
На главной диагонали находятся коэффициенты Метод состоит из двух этапов: прямой и обратной прогонки. При прямой прогонке каждое
Из первого уравнения системы получим
с другой стороны,
Следовательно,
Из второго уравнения получим
с другой стороны,
Обозначим
тогда
Аналогично для любого
Обратная прогонкасостоит в последовательном вычислении неизвестных
с другой стороны,
Умножим второе уравнения на
Отсюда получим:
Далее неизвестные вычисляются по формуле
Необходимо отметить возможность появления деления на нуль в формулах. Доказано, что если Метод простых итераций Выразим неизвестные в системе (4.1) и представим в следующем виде:
Зададим начальные приближения для
где k – номер итерации. Итерационный процесс продолжается до тех пор, пока не будет выполнено следующее условие:
где n –количество уравнений. Если условие не выполняется, итерации повторяются, приняв
Для того чтобы не проверять условие для всех уравнений, условие окончания итераций можно записать в следующем виде:
Метод Ньютона-Рафсона Метод Ньютона-Рафсона обладает более быстрой сходимостью. В основе метода лежит использование разложения функций в ряд Тейлора, причем члены, содержащие вторые и более высоких порядков производные, отбрасываются. Будем рассматривать систему нелинейных уравнений также в общем виде. Пусть точное значение корней системы равно
Проведем разложение левых частей уравнений в ряд Тейлора, ограничиваясь лишь первыми членами относительно приращений:
…
Поскольку левые части уравнений равны нулю, то приравниваем нулю и правые части. В результате получим систему линейных уравнений (4.3)относительно приращений
…
Производные вычисляются в точках Матрица системы записывается следующим образом:
Такая матрица называется матрицей Якоби, а определитель – якобианом. Для существования единственного решения необходимо и достаточно чтобы Производная рассчитывается следующим образом: задаются начальные приближения Лабораторная работа 2 Применение метода простых итераций для решения систем линейных и систем нелинейных уравнений Цель работы: изучить метод простых итераций для решения системы линейных и системы нелинейных уравнений, формулы для вычисления, написать программу на языке программирования для реализации данного метода. Ход решения: 1. Написать программу и ввести начальные данные согласно условиям задачи. Начальные данные должны соответствовать начальным приближениям для вычисления неизвестных (корней). 2. Вывести на экран результат программы, т.е. вывести найденные неизвестные – корни систем уравнений. Варианты заданий Задание 1. Решить систему линейных алгебраических уравнений методом простых итераций:
Задание 2. Решить систему нелинейных уравнений методом простых итераций:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 452; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.0.21 (0.022 с.) |

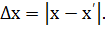
 – это отношение абсолютной погрешности к модулю приближенного значения
– это отношение абсолютной погрешности к модулю приближенного значения 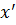 :
: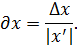
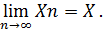
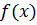 и требуется найти все или некоторые значения
и требуется найти все или некоторые значения 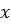 , для которых
, для которых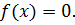 (1.1)
(1.1) , при котором
, при котором 
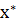 уравнения называется простым, если первая производная функции
уравнения называется простым, если первая производная функции 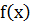 в точке
в точке 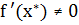 . Если же
. Если же 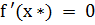 , то корень x* называется кратным.
, то корень x* называется кратным.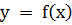 с осью абсцисс.
с осью абсцисс.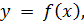 имеющей четыре корня: два простых (
имеющей четыре корня: два простых (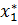 и
и 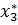 ) и два кратных (
) и два кратных (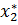 и
и 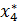 ).
).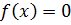 , где функция непрерывна на отрезке
, где функция непрерывна на отрезке 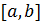 и единственный корень
и единственный корень 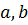 пополам и получим
пополам и получим 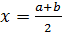 .
.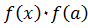 . Если знак условия положителен, то корень уравнения находится на отрезке
. Если знак условия положителен, то корень уравнения находится на отрезке 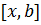 и левая граница интервала перемещается в точку
и левая граница интервала перемещается в точку 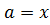 . Если знак условия отрицателен, то корень уравнения находится на отрезке
. Если знак условия отрицателен, то корень уравнения находится на отрезке 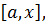 т.е.
т.е. 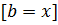 .
.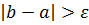 .
.
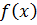
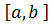 сходимость гарантирована. Кроме того, простота реализации метода уменьшает число вспомогательных операций и частично компенсирует невысокое быстродействие.
сходимость гарантирована. Кроме того, простота реализации метода уменьшает число вспомогательных операций и частично компенсирует невысокое быстродействие.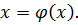 (2.1)
(2.1)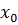 и подставим его в правую часть уравнения (2.1). На этом шаге мы получим уточненное значение
и подставим его в правую часть уравнения (2.1). На этом шаге мы получим уточненное значение  .Подставим теперь
.Подставим теперь 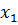 в уравнение (2.1) и получим новое приближение
в уравнение (2.1) и получим новое приближение 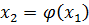 и т. д.
и т. д.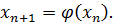 (2.2)
(2.2)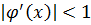 .Это условие является необходимым и достаточным. При
.Это условие является необходимым и достаточным. При 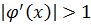 внезависимости от выбора начального приближения процесс будет расходиться.
внезависимости от выбора начального приближения процесс будет расходиться.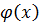 в граничных точках интервала
в граничных точках интервала 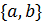 , содержащего корень, и за начальное приближение принимают тот конец интервала, для которого выполняется условие
, содержащего корень, и за начальное приближение принимают тот конец интервала, для которого выполняется условие 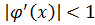 .
.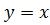 и
и 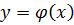 . Абсцисса точек пересечения этих графиков является корнем уравнения
. Абсцисса точек пересечения этих графиков является корнем уравнения 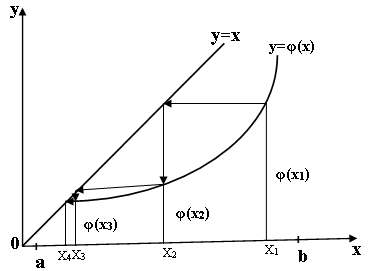
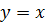 и
и 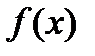 в точке начального приближения
в точке начального приближения 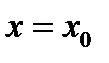 касательной, пересечение которой с осью
касательной, пересечение которой с осью 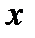 дает первое приближение x 1и т.д. (рис. 2.3).
дает первое приближение x 1и т.д. (рис. 2.3).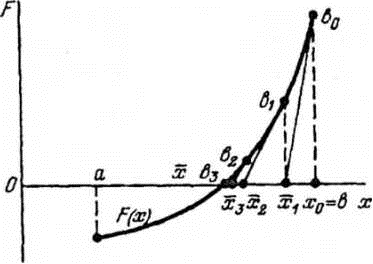
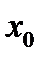 , имеет вид
, имеет вид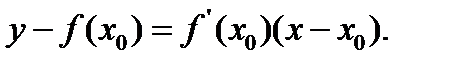
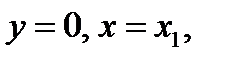
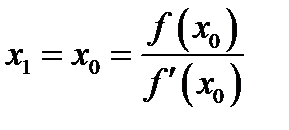 .
.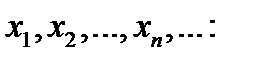
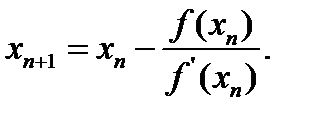
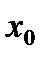 выбирают тот конец отрезка
выбирают тот конец отрезка 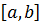 , для которого выполняется условие
, для которого выполняется условие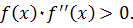
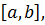 а первая и вторая производные функции определены, непрерывны и сохраняют постоянные знаки на этом интервале.
а первая и вторая производные функции определены, непрерывны и сохраняют постоянные знаки на этом интервале.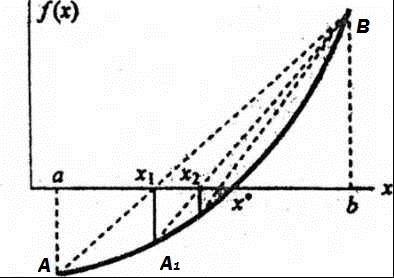
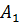 . Затем проводим новую хорду через точки
. Затем проводим новую хорду через точки 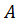 и
и 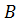 и т.д.
и т.д.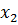 , имеет вид
, имеет вид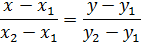
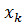 – это точка пересечения хорды с осью
– это точка пересечения хорды с осью 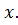 Следовательно, в уравнении прямой
Следовательно, в уравнении прямой 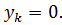
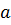 ), другой конец
), другой конец 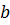 – неподвижный. Условием сходимости итерационного процесса является правильный выбор подвижного и неподвижного концов. Обозначим подвижный конец интервала
– неподвижный. Условием сходимости итерационного процесса является правильный выбор подвижного и неподвижного концов. Обозначим подвижный конец интервала 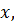 неподвижный конец –
неподвижный конец – 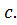
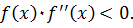
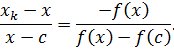
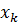 , и это будет итерационной формулой метода:
, и это будет итерационной формулой метода: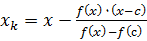 .
.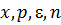
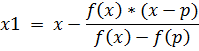
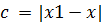
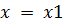
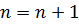
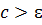
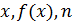
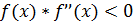 уравнения.
уравнения.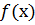 на выходе программы должно быть максимально близким к 0, результаты каждого метода должны быть приближенно равными между собой.
на выходе программы должно быть максимально близким к 0, результаты каждого метода должны быть приближенно равными между собой.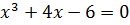
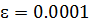
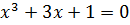
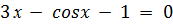
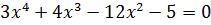
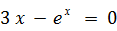
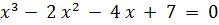

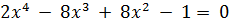
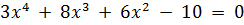
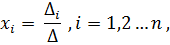
 – определитель системы,
– определитель системы, 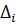 – определители, получающиеся из определителя
– определители, получающиеся из определителя 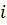 – го столбца столбцом свободных членов.
– го столбца столбцом свободных членов.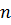 линейных уравнений сводится к вычислению
линейных уравнений сводится к вычислению 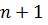 определителя порядка
определителя порядка 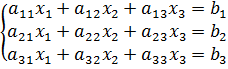 .
.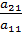 и вычтем его из второго уравнения. Затем полученное уравнение поставим вместо второго. Тогда первый коэффициент полученного второго уравнения станет равным нулю. То же самое проделаем с третьим уравнением, умножив исходное первое уравнение на
и вычтем его из второго уравнения. Затем полученное уравнение поставим вместо второго. Тогда первый коэффициент полученного второго уравнения станет равным нулю. То же самое проделаем с третьим уравнением, умножив исходное первое уравнение на 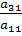 . В результате система будет преобразована к следующему виду:
. В результате система будет преобразована к следующему виду: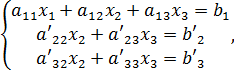
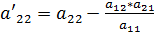 ,
, 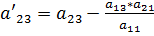 ,
, 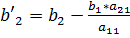 ,
,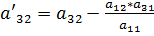 ,
, 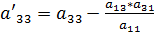 ,
, 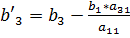 .
.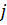 – номер столбца.
– номер столбца.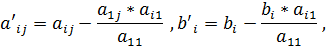
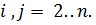
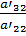 и вычтем его из третьего. В результате получим
и вычтем его из третьего. В результате получим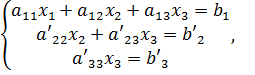
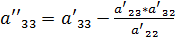 ,
, 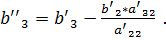
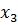 , затем подставить его во второе уравнение и найти из него
, затем подставить его во второе уравнение и найти из него 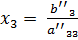 ,
, 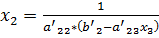 ,
,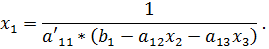
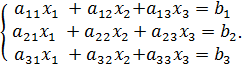
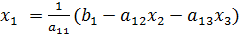 ;
;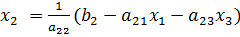 ;
;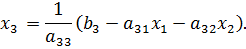
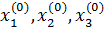 , подставляя которые, мы получим новое приближение:
, подставляя которые, мы получим новое приближение: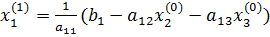 ;
;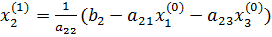 ;
;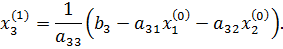
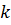 – номер итерации, тогда для
– номер итерации, тогда для 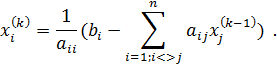
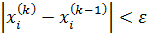 ,
, 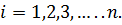
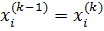 .
.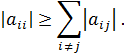
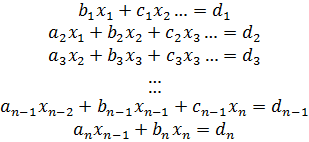
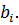
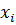 выражается через
выражается через 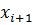 с помощью прогоночных коэффициентов
с помощью прогоночных коэффициентов 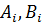 :
: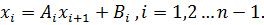
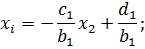
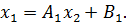
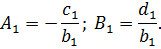
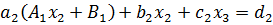 ;
;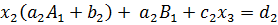 ;
;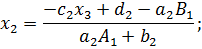
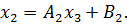
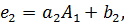
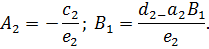
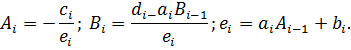
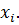 Вычислим
Вычислим 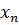 из последнего уравнения:
из последнего уравнения: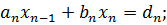
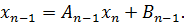
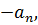 вычтем его из первого, получим
вычтем его из первого, получим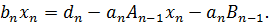
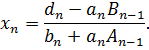
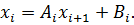
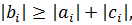 причем, хотя бы при одном
причем, хотя бы при одном 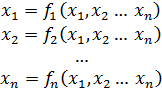 (4.2)
(4.2)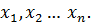 Подставим их в правую часть системы (4.2) и получим значения неизвестных в следующей итерации:
Подставим их в правую часть системы (4.2) и получим значения неизвестных в следующей итерации: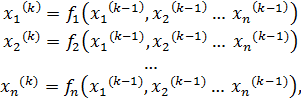
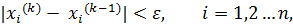
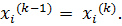
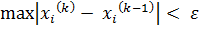 ,
, 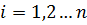 .
.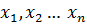 , а приближенные значения –
, а приближенные значения – 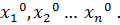 Тогда имеем:
Тогда имеем: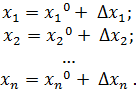
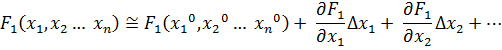
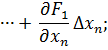
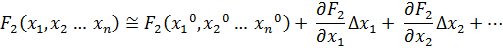
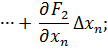
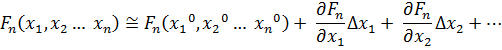
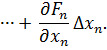
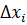 :
: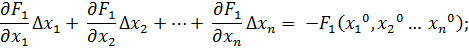
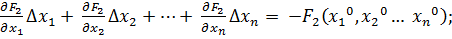 (4.3)
(4.3)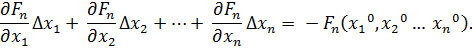
 .
.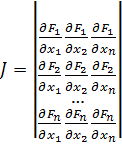
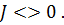
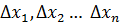 , пока
, пока 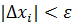 .
.