
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 3. Решение систем линейных алгебраических уравнений
Система линейных алгебраических уравнений (СЛАУ), состоящая из n уравнений, может быть записана в следующем виде
или может быть представлена в матричной форме: где
Для СЛАУ Решением СЛАУ является такая совокупность значений неизвестных Диагональ матрицы, проходящая слева направо, называется главной диагональю. Если все элементы матрицы, находящиеся ниже главной диагонали, равны нулю, то такая матрица называется треугольной. Необходимым и достаточным условием существования единственного решения системы линейных уравнений является неравенство нулю определителя матрицы коэффициентов. В случае равенства нулю определителя матрица называется вырожденной. При этом система либо не имеет решения, либо имеет их бесконечное множество. Система, в которой определитель близок, но не равен нулю, называется плохо обусловленной системой. Непосредственный расчет определителей для больших В настоящее время известны многочисленные приближенные методы решения систем линейных алгебраических уравнений, которые делятся на две большие группы: прямые методы и методы итераций. Прямые методы всегда гарантируют получение решения, если оно существует, однако, для больших Рассмотрим наиболее распространенные методы. Метод Крамера Метод Крамера является прямым методом. Это способ решения систем линейных алгебраических уравнений с числом уравнений равным количеству неизвестных с ненулевым главным определителем матрицы, коэффициентов системы. Обычно метод Крамера применяется для систем с очень малым количеством уравнений. Решение представляется в виде
где
Система
Метод Гаусса Метод Гаусса принадлежит к группе прямых методов и является классическим методом решения системы линейных алгебраических уравнений. Метод основан на приведении матрицы к треугольному виду. Рассмотрим этот метод на примере системы трех уравнений, а затем распространим его на систему
Умножим первое уравнение на
где
Обобщим эти формулы для системы
где Теперь из третьего уравнения необходимо исключить член, содержащий
где
Теперь матрица системы приведена к треугольному виду, и из третьего уравнения можно найти
Аналогично строится алгоритм для системы с произвольным числом уравнений, который включает два этапа: 1. Прямой ход – приведение матрицы системы к треугольному виду. 2. Обратный ход – вычисление искомых неизвестных. Метод простых итераций Метод простых итераций является одним из простейших итерационных методов. Рассмотрим метод также на примере трех линейных уравнений, а затем применим на систему
Предполагается, что диагональные элементы отличны от нуля, в противном случае надо переставить уравнения. Выразим неизвестные из уравнений
Зададим некоторые начальные (нулевые) приближения:
Обозначим через
Итерации проводятся до тех пор, пока не будет выполнено следующее условие:
Если условие не выполняется, итерации повторяют, приняв
Для сходимости итерационного процесса достаточно, чтобы модули диагональных коэффициентов были не меньше сумм модулей всех остальных коэффициентов:
Это условие является достаточным для сходимости метода итерации, но не является необходимым, т.е. для некоторых систем процесс сходится и при нарушении этого условия. В случае системы линейных уравнений, чтобы получить сходимость и верное решение, необходимо соблюдать условие – на главной диагонали системы должны располагаться максимальные элементы каждой строки (т.е. при необходимости надо переставить строки местами). Метод прогонки Метод прогонки используется для решения систем линейных уравнений с трехдиагональной матрицей:
На главной диагонали находятся коэффициенты Метод состоит из двух этапов: прямой и обратной прогонки. При прямой прогонке каждое
Из первого уравнения системы получим
с другой стороны,
Следовательно,
Из второго уравнения получим
с другой стороны,
Обозначим
тогда
Аналогично для любого
Обратная прогонкасостоит в последовательном вычислении неизвестных
с другой стороны,
Умножим второе уравнения на
Отсюда получим:
Далее неизвестные вычисляются по формуле
Необходимо отметить возможность появления деления на нуль в формулах. Доказано, что если
|
||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 287; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.82.23 (0.035 с.) |
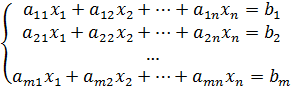
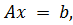
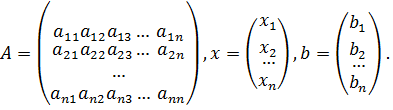
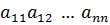 – это постоянные коэффициенты,
– это постоянные коэффициенты, 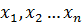 – неизвестные,
– неизвестные, 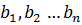 – свободные члены системы.
– свободные члены системы.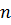 (матриц)является очень трудоемким по сравнению с вычислительными методами.
(матриц)является очень трудоемким по сравнению с вычислительными методами.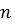 требуется большое количество операций, и возникает опасность накопления погрешностей. Этого недостатка лишены итерационные методы, но зато они не всегда сходятся и могут применяться, лишь для систем определенных классов.
требуется большое количество операций, и возникает опасность накопления погрешностей. Этого недостатка лишены итерационные методы, но зато они не всегда сходятся и могут применяться, лишь для систем определенных классов.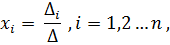
 – определитель системы,
– определитель системы, 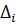 – определители, получающиеся из определителя
– определители, получающиеся из определителя 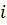 – го столбца столбцом свободных членов.
– го столбца столбцом свободных членов.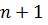 определителя порядка
определителя порядка 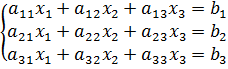 .
.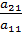 и вычтем его из второго уравнения. Затем полученное уравнение поставим вместо второго. Тогда первый коэффициент полученного второго уравнения станет равным нулю. То же самое проделаем с третьим уравнением, умножив исходное первое уравнение на
и вычтем его из второго уравнения. Затем полученное уравнение поставим вместо второго. Тогда первый коэффициент полученного второго уравнения станет равным нулю. То же самое проделаем с третьим уравнением, умножив исходное первое уравнение на 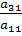 . В результате система будет преобразована к следующему виду:
. В результате система будет преобразована к следующему виду: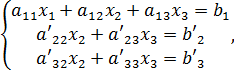
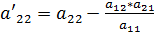 ,
, 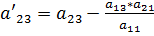 ,
, 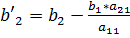 ,
,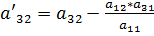 ,
, 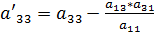 ,
, 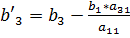 .
.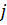 – номер столбца.
– номер столбца.
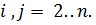
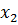 . Для этого умножим второе уравнение на
. Для этого умножим второе уравнение на 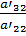 и вычтем его из третьего. В результате получим
и вычтем его из третьего. В результате получим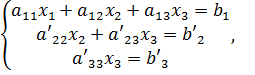
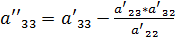 ,
, 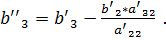
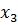 , затем подставить его во второе уравнение и найти из него
, затем подставить его во второе уравнение и найти из него 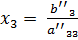 ,
, 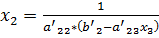 ,
,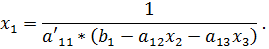
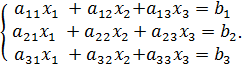
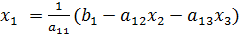 ;
;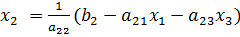 ;
;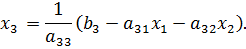
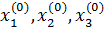 , подставляя которые, мы получим новое приближение:
, подставляя которые, мы получим новое приближение: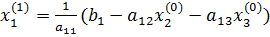 ;
;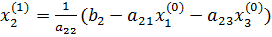 ;
;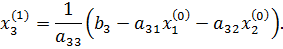
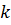 – номер итерации, тогда для
– номер итерации, тогда для 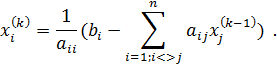
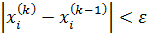 ,
, 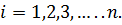
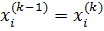 .
.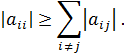
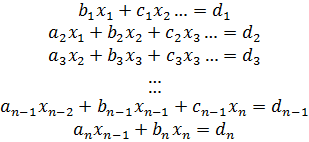
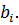
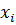 выражается через
выражается через 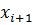 с помощью прогоночных коэффициентов
с помощью прогоночных коэффициентов 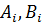 :
: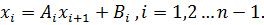
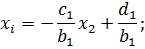
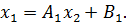
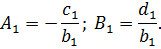
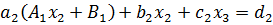 ;
;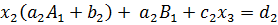 ;
;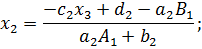
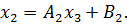
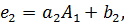
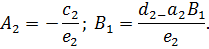
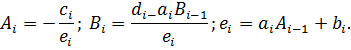
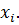 Вычислим
Вычислим 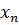 из последнего уравнения:
из последнего уравнения: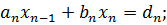
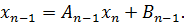
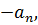 вычтем его из первого, получим
вычтем его из первого, получим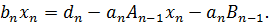
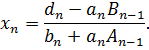
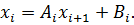
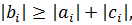 причем, хотя бы при одном
причем, хотя бы при одном 


