
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 8. Численное решение обыкновенных дифференциальных уравненийСодержание книги
Поиск на нашем сайте Решение дифференциальных уравнений является одной из важнейших математических задач. Обыкновенными дифференциальными уравнениями(ОДУ) называются уравнения, которые содержат одну или несколько производных от искомой функции
где Наивысший порядок Уравнение первого порядка можно записать в виде
Решением дифференциального уравнения (8.1) называется всякая функция Общее решение ОДУ
Частное решение ОДУ получается из общего, если произвольным постоянным придать определенные значения. Для уравнения первого порядка общее решение зависит от одной произвольной постоянной:
Если постоянная принимает определенное значение
Чтобы выделить одно решение, задают начальное условие:
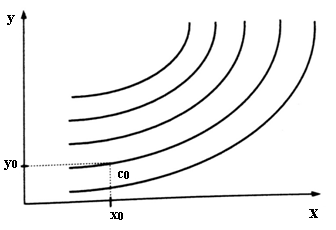
На рис. 8.1 представлено общее решение уравнения первого порядка – семейство интегральных кривых. Частным решением, согласно теореме Коши, является кривая, проходящая через точку
Рис. 8.1.
Рассмотрим теорему Коши. Если правая часть Задача Коши Задача Коши заключается в отыскании функции Обычно определяют решение задачи Коши на отрезке, расположенном справа от начального значения Наиболее распространенными численными методами решения дифференциальных уравнений являются методы конечных разностей. Сущность этих методов состоит в том, что область непрерывного изменения аргумента и функции заменяется дискретным множеством точек, называемых узлами. Эти узлы составляют разностную сетку. Искомая функция непрерывного аргумента приближенно заменяется функцией дискретного аргумента на заданной сетке. Эта функция называется сеточной. Исходное дифференциальное уравнение заменяется разностным уравнением, т.е. производные заменяются конечноразностными отношениями. Численными методами решаются не только отдельные уравнения, но и системы уравнений (чаще всего первого порядка), причем большинство методов решения одного уравнения легко распространяются на решение систем. Метод Эйлера Метод Эйлера – наиболее простой численный метод решения (систем) обыкновенных дифференциальных уравнений. Он имеет первый порядок точности. Метод реализуется следующим алгоритмом. Задано уравнение
и начальные условия: Значения функции в узлах Для простоты примем постоянным шаг
Заменим производную конечно-разностным отношением
Отсюда получаем
Зная значение функции в начальной точке Метод Рунге-Кутта Метод Рунге-Кутта является наиболее распространенным методом решения обыкновенных дифференциальных уравнений. Существуют разностные схемы разного порядка точности, построенные на основе этого метода. Приведем метод четвертого порядка:
Данный метод требует на каждом шаге четырехкратного вычисления правой части уравнения, но это окупается повышенной точностью, что дает возможность производить расчет с более крупным шагом. Алгоритм расчета подобен алгоритму расчета Эйлера. Разница в том, что внутри цикла сначала вычисляются Приведем формулы Рунге–Кутта для системы двух уравнений:
С начальными условиями при Формулы имеют вид:
Аналогично можно записать формулы Рунге–Кутта для систем из трех и более уравнений. Алгоритм решения аналогичен алгоритму решения системы уравнений методом Эйлера.
|
||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 185; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

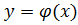 . Их можно записать в виде
. Их можно записать в виде (8.1)
(8.1)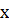 – независимая переменная.
– независимая переменная.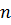 , входящей в уравнение производной, определяет порядок дифференциального уравнения.
, входящей в уравнение производной, определяет порядок дифференциального уравнения.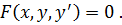
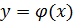 , которая после ее подстановки в уравнение превращает его в тождество.
, которая после ее подстановки в уравнение превращает его в тождество.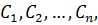 т.е. общее решение уравнения (8.1) имеет вид
т.е. общее решение уравнения (8.1) имеет вид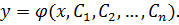
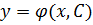 .
.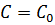 , то получим частное решение:
, то получим частное решение: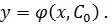
 (8.2)
(8.2)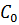 .
.
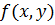 уравнения
уравнения 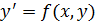 и ее частная производная
и ее частная производная 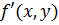 определены и непрерывны в некоторой области
определены и непрерывны в некоторой области 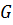 изменения переменных
изменения переменных 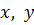 , то для всякой внутренней точки
, то для всякой внутренней точки 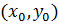 этой области данное уравнение имеет единственное решение, принимающее заданное значение
этой области данное уравнение имеет единственное решение, принимающее заданное значение  при
при 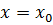 .
.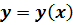 , удовлетворяющей уравнению
, удовлетворяющей уравнению 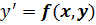 и начальному условию(8.2).
и начальному условию(8.2).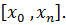
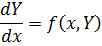
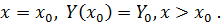
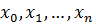 заменим сеточной функцией
заменим сеточной функцией  .
.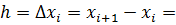
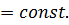
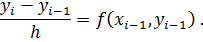
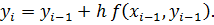
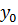 ,последовательно можно найти значения функции во всех точках сетки.
,последовательно можно найти значения функции во всех точках сетки.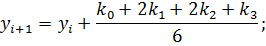
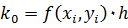 ;
;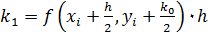 ;
;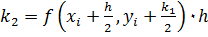 ;
;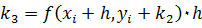 .
.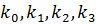 а затем – значение
а затем – значение 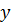 в новом расчетном узле.
в новом расчетном узле.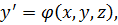
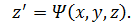
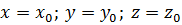 .
.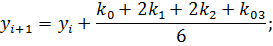
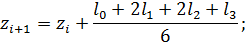
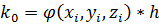 ;
;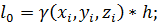
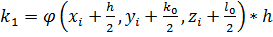 ;
;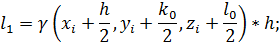
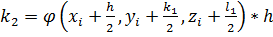 ;
;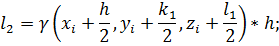
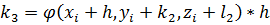 ;
;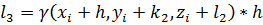 .
.


