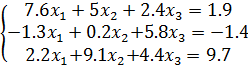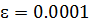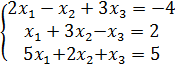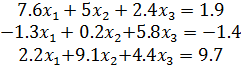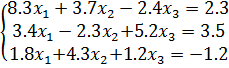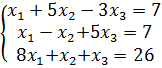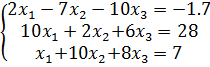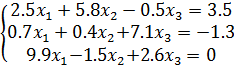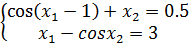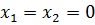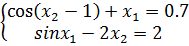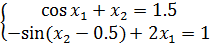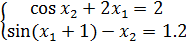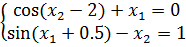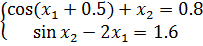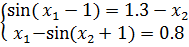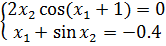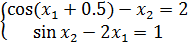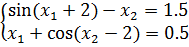Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 4. Решение систем нелинейных уравненийСодержание книги
Поиск на нашем сайте Запишем систему нелинейных уравнений в общем виде
На данный момент не существует прямых методов решения систем нелинейных уравнений в общем виде. Однако для решения часто используются итерационные методы. Метод простых итераций Выразим неизвестные в системе (4.1) и представим в следующем виде:
Зададим начальные приближения для
где k – номер итерации. Итерационный процесс продолжается до тех пор, пока не будет выполнено следующее условие:
где n –количество уравнений. Если условие не выполняется, итерации повторяются, приняв
Для того чтобы не проверять условие для всех уравнений, условие окончания итераций можно записать в следующем виде:
Метод Ньютона-Рафсона Метод Ньютона-Рафсона обладает более быстрой сходимостью. В основе метода лежит использование разложения функций в ряд Тейлора, причем члены, содержащие вторые и более высоких порядков производные, отбрасываются. Будем рассматривать систему нелинейных уравнений также в общем виде. Пусть точное значение корней системы равно
Проведем разложение левых частей уравнений в ряд Тейлора, ограничиваясь лишь первыми членами относительно приращений:
…
Поскольку левые части уравнений равны нулю, то приравниваем нулю и правые части. В результате получим систему линейных уравнений (4.3)относительно приращений
…
Производные вычисляются в точках Матрица системы записывается следующим образом:
Такая матрица называется матрицей Якоби, а определитель – якобианом. Для существования единственного решения необходимо и достаточно чтобы Производная рассчитывается следующим образом: задаются начальные приближения Лабораторная работа 2 Применение метода простых итераций для решения систем линейных и систем нелинейных уравнений Цель работы: изучить метод простых итераций для решения системы линейных и системы нелинейных уравнений, формулы для вычисления, написать программу на языке программирования для реализации данного метода. Ход решения: 1. Написать программу и ввести начальные данные согласно условиям задачи. Начальные данные должны соответствовать начальным приближениям для вычисления неизвестных (корней). 2. Вывести на экран результат программы, т.е. вывести найденные неизвестные – корни систем уравнений. Варианты заданий Задание 1. Решить систему линейных алгебраических уравнений методом простых итераций:
Задание 2. Решить систему нелинейных уравнений методом простых итераций:
Входные данные, после запуска программы – начальные приближения и точность вычисления. Выходные данные – корни систем уравнений и проверка (подстановка найденных значений в исходные уравнения).
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 287; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

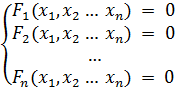 . (4.1)
. (4.1)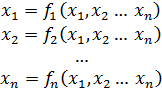 (4.2)
(4.2)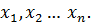 Подставим их в правую часть системы (4.2) и получим значения неизвестных в следующей итерации:
Подставим их в правую часть системы (4.2) и получим значения неизвестных в следующей итерации: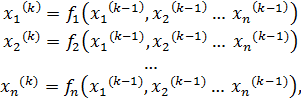
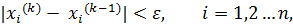
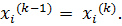
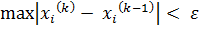 ,
, 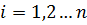 .
.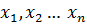 , а приближенные значения –
, а приближенные значения – 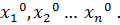 Тогда имеем:
Тогда имеем: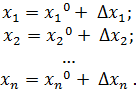
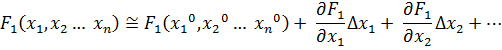
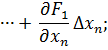
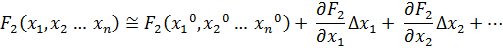
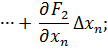
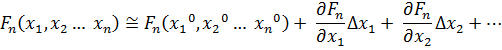
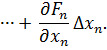
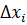 :
: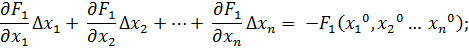
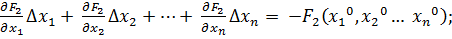 (4.3)
(4.3)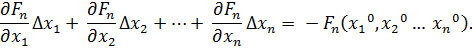
 .
.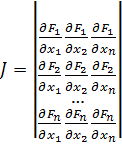
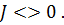
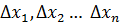 , пока
, пока 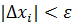 .
.