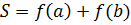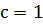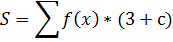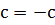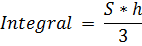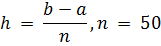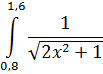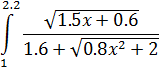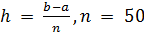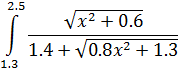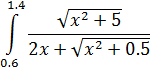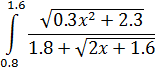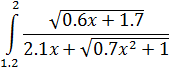Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление определенных интегралов с помощьюСодержание книги
Поиск на нашем сайте Численных методов Цель работы: изучить методы численного интегрирования, алгоритм каждого метода, формулы для вычисления, написать программу на языке программирования для реализации данных методов. К методам численного интегрирования относят метод прямоугольников (левых, правых, средних), метод трапеций и метод парабол (метод Симпсона). Алгоритм метода прямоугольников:
Ввод
Fo
Next
Печать Алгоритм метода трапеций:
Ввод
For
Next
Печать Алгоритм метода Симпсона:
Ввод
For
Next
Печать Варианты заданий
Входные данные после запуска программы – значения границ Выходные данные – вычисленное значение интеграла по каждому из четырех методов. Реализация алгоритмов на языке C#. При вычислении определенных интегралов с помощью численных методов в основной части программы определяются верхний и нижний пределы интегрирования, количество интегралов разбиения, а для вычисления подынтегральной функции используется отдельный метод: Static double func(double x) { return (Math.Sqrt(1.5 * x + 0.6)) / (1.6 + Math.Sqrt(0.8 * Math.Pow(x, 2) + 2)); } Поскольку реализация алгоритма метода прямоугольников (левых и правых) и алгоритма метода трапеций одинакова, то вычисление можно организовать в одном цикле, при этом метод средних прямоугольников требует дополнительных условий. int n = 50; double H = (b - a) / n; for (double x = a; x < b; x += H) { result1 += func(x) * H; //левых прямоугольников result2 += func(x + H) * H; //правых прямоугольников result3 += H * (func(x) + func(x + H)) / 2; //трапеций } for (double i = a; i< b - H; i = i + H) { result4 = result4 + (func(i) + func(i + H)) / 2; //средних прямоугольников } Формула для вычисления функции по методу Симпсона достаточно громоздка, поэтому для удобства следует разбить ее на части, каждую из которых можно вычислить с помощью цикла с параметром FOR. Реализация данного метода представлена ниже: // метод Симпсона Static double Simpson(double a, double b, int n) { Int i; double S = 0; double[] x = new double[n + 1]; double h = (b - a) / n; // значение функции для равноотстоящих точек for (i = 0; i < n; i++) { x[i] = a + h * i; } // для подсчета h/3 * (y0+yn) S = h * (func(x[0])+func(x[n])) / 3; // для подсчета h/3 * 4(y1+y3+...+y(n-1)) for (i = 1; i< (n - 1); i = i + 2) { S = S + h * 4 * func(x[i]) / 3; } // для подсчета h/3 * 2(y2+y4+...+y(n-2)) for (i = 2; i< (n - 2); i = i + 2) { S = S + h * 2 * func(x[i]) / 3; } return S; } Контрольные вопросы 1. Особенности численного интегрирования. 2. Метод левых, правых и средних прямоугольников. 3. Метод трапеций. 4. Метод парабол. 5. Число участков разбиения и шаг интегрирования. 6. Способ повышения точности при численном интегрировании.
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 298; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

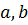 – соответственно нижний и верхний пределы интегрирования;
– соответственно нижний и верхний пределы интегрирования;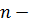 количество участков разбиения;
количество участков разбиения;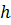 – шаг;
– шаг;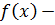 подынтегральная функция.
подынтегральная функция.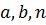
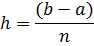
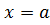 r to
r to 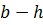 step
step 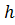

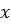
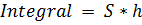

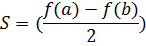
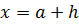 to
to