
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 2. Решение алгебраических и трансцендентных уравнений
К основным численным методам решения уравнений относятся такие методы, как метод половинного деления, метод простых итераций, метод касательных и метод хорд. Одним из основных численных методов является метод итераций, на принципах которого основаны остальные методы. Прежде чем использовать какой-либо численный метод, необходимо произвести отделение корней, т.е. определить количество корней в интересующей нас области и выделить достаточно малые интервалы, в каждом из которых заключен только один корень. Условием существования корня непрерывной функции на интервале является
что говорит о том, что на данном интервале функция изменяет знак, т.е. пересекает ось Метод половинного деления Метод половинного деления (дихотомии, бисекции) является самым простым и надежным способом решений нелинейного решения. Метод реализуется следующим алгоритмом. Пусть необходимо решить уравнение Вычислим значение функции в этой точке (рис.2.1) и проверим знак условия Далее продолжаем вышеописанные шаги, т.е. новый отрезок вновь делим пополам и производим новый выбор. Процесс повторяем до тех пор, пока длина отрезка не станет меньше заданной точности
Рис. 2.1. График функции Число итераций при использовании этого метода значительно, и поэтому сходимость его медленная. Однако при любой ширине отрезка Метод простых итераций Метод простых итераций является популярным способом численного решения математических задач. Его суть – нахождение алгоритма поиска по известному приближению (приближенному значению) искомой величины следующего, более точного приближения. Метод реализуется следующим алгоритмом. Пусть уравнение
Выберем на отрезке Продолжая этот процесс неограниченно, получим последовательность приближений к корню:
Процесс итераций сходится при условии Для выбора начального приближения вычисляют значения первых производных функции Геометрически способ простых итераций можно представить следующим образом. Построим графики двух функций:
Рис. 2.2. Графики функций: 2.3. Метод касательных (Ньютона) Метод касательных (Ньютона) является наиболее эффективным методом решения нелинейных уравнений. Метод основан на замене
Рис. 2.3. График функции Уравнение касательной, проходящей через точку
Первое пересечение получим, взяв абсциссу точки пересечения этой касательной с осью OX, т. е.
Аналогично поступаем с остальными точками и в результате получаем последовательность
Метод обеспечивает быструю (квадратичную) сходимость. В качестве первого приближения
Это условие сходимости является достаточным, но необходимым, т.е. если условие выполняется, то итерационный процесс обязательно сойдется, а если не выполняется, то может или сойтись, или не сойтись.
Метод хорд Метод хорд является итерационным численным методом приближённого нахождения корня уравнения. Метод реализуется следующим алгоритмом. Пусть уравнение
Рассмотрим геометрическое представление метода (рис. 2.4).
Рис. 2.4. График функции Проведем хорду через точки A и B. В точке пересечения хорды с осью Уравнение прямой, проходящей через две точки
Из этого уравнения необходимо определить точку Один из концов отрезка В качестве подвижного конца выбирается точка, для которой выполняется условие
Уравнение (2.3) можно записать в следующем виде:
Отсюда можно найти искомую точку
Условие сходимости итерационного процесса является достаточным, но не необходимым.
|
||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 300; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.38.125 (0.019 с.) |
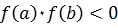 ,
,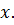
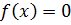 , где функция непрерывна на отрезке
, где функция непрерывна на отрезке 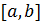 и единственный корень
и единственный корень 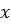 заключен в том же интервале. Разделим отрезок
заключен в том же интервале. Разделим отрезок 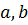 пополам и получим
пополам и получим 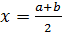 .
.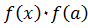 . Если знак условия положителен, то корень уравнения находится на отрезке
. Если знак условия положителен, то корень уравнения находится на отрезке 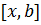 и левая граница интервала перемещается в точку
и левая граница интервала перемещается в точку 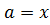 . Если знак условия отрицателен, то корень уравнения находится на отрезке
. Если знак условия отрицателен, то корень уравнения находится на отрезке 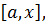 т.е.
т.е. 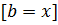 .
.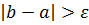 .
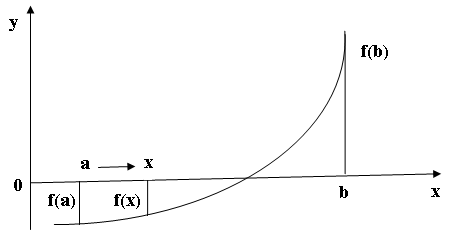
.
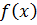
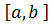 сходимость гарантирована. Кроме того, простота реализации метода уменьшает число вспомогательных операций и частично компенсирует невысокое быстродействие.
сходимость гарантирована. Кроме того, простота реализации метода уменьшает число вспомогательных операций и частично компенсирует невысокое быстродействие.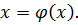 (2.1)
(2.1)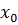 и подставим его в правую часть уравнения (2.1). На этом шаге мы получим уточненное значение
и подставим его в правую часть уравнения (2.1). На этом шаге мы получим уточненное значение  .Подставим теперь
.Подставим теперь 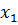 в уравнение (2.1) и получим новое приближение
в уравнение (2.1) и получим новое приближение 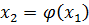 и т. д.
и т. д.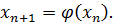 (2.2)
(2.2)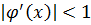 .Это условие является необходимым и достаточным. При
.Это условие является необходимым и достаточным. При 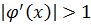 внезависимости от выбора начального приближения процесс будет расходиться.
внезависимости от выбора начального приближения процесс будет расходиться.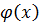 в граничных точках интервала
в граничных точках интервала 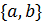 , содержащего корень, и за начальное приближение принимают тот конец интервала, для которого выполняется условие
, содержащего корень, и за начальное приближение принимают тот конец интервала, для которого выполняется условие 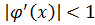 .
.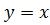 и
и 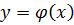 . Абсцисса точек пересечения этих графиков является корнем уравнения
. Абсцисса точек пересечения этих графиков является корнем уравнения 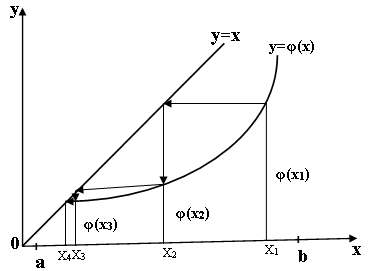
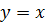 и
и 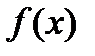 в точке начального приближения
в точке начального приближения 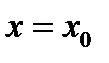 касательной, пересечение которой с осью
касательной, пересечение которой с осью 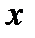 дает первое приближение x 1и т.д. (рис. 2.3).
дает первое приближение x 1и т.д. (рис. 2.3).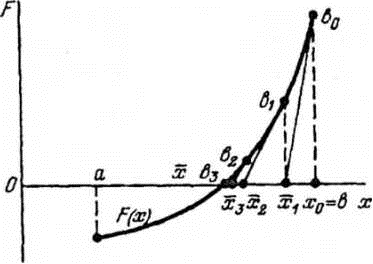
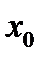 , имеет вид
, имеет вид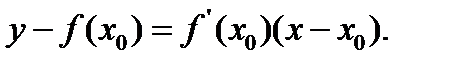
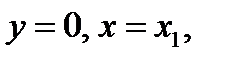
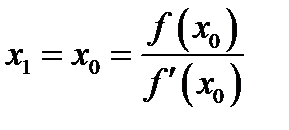 .
.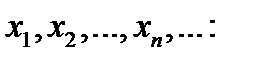
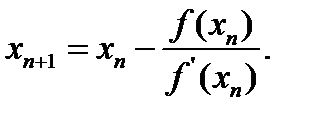
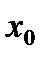 выбирают тот конец отрезка
выбирают тот конец отрезка 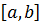 , для которого выполняется условие
, для которого выполняется условие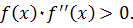
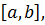 а первая и вторая производные функции определены, непрерывны и сохраняют постоянные знаки на этом интервале.
а первая и вторая производные функции определены, непрерывны и сохраняют постоянные знаки на этом интервале.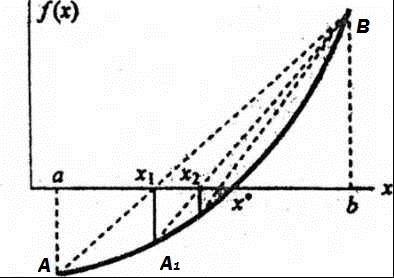
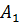 . Затем проводим новую хорду через точки
. Затем проводим новую хорду через точки 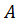 и
и 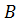 и т.д.
и т.д.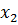 , имеет вид
, имеет вид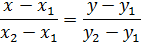
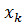 – это точка пересечения хорды с осью
– это точка пересечения хорды с осью 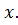 Следовательно, в уравнении прямой
Следовательно, в уравнении прямой 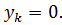
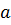 ), другой конец
), другой конец 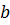 – неподвижный. Условием сходимости итерационного процесса является правильный выбор подвижного и неподвижного концов. Обозначим подвижный конец интервала
– неподвижный. Условием сходимости итерационного процесса является правильный выбор подвижного и неподвижного концов. Обозначим подвижный конец интервала 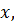 неподвижный конец –
неподвижный конец – 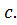
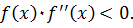
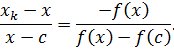
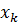 , и это будет итерационной формулой метода:
, и это будет итерационной формулой метода: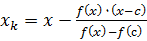 .
.


