
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 7. Численное интегрированиеСодержание книги
Поиск на нашем сайте Во многих случаях, когда функция задана аналитически, определенный интеграл вычисляется по формуле Ньютона – Лейбница, которая состоит в том, что определенный интеграл равен приращению первообразной
Однако на практике не всегда можно вычислить интеграл с помощью этой формулы. Основными причинами являются: 1. Невозможность выразить первообразную функцию 2. Первообразная 3. Функция В случае, когда нельзя применить формулу Ньютона–Лейбница, обращаются к методам численного интегрирования. Методы численного интегрирования основаны на аппроксимации подынтегральной функции некоторыми более простыми выражениями, т.е. подынтегральную функцию Например, можно заменить подынтегральную функцию интерполяционным многочленом. К методам численного интегрирования относят такие методы как: метод прямоугольников (левых, правых, средних), трапеций, парабол (метод Симпсона). Рассмотри каждый из методов подробнее.
Метод прямоугольников Метод прямоугольников является одним из простейших методов. Данный метод использует замену определённого интеграла интегральной суммой. Формулу прямоугольников можно получить из геометрической интерпретации интеграла. Будем интерпретировать следующий интеграл:
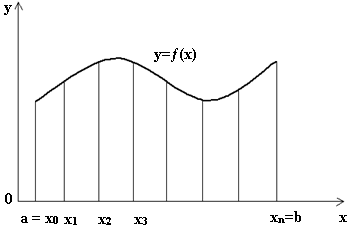
как площадь криволинейной трапеции, ограниченной графиком функции Разобьем отрезок
Рис. 7.1. Разделение отрезка Заменим приближенно площадь криволинейной трапеции площадью ступенчатой фигуры, как показано на рис.7.2.
Рис. 7.2. Ступенчатая фигура Эта фигура состоит из Для левых прямоугольников с постоянным шагом (рис.7.3).
Рис. 7.3 Иллюстрация метода левых прямоугольников
Для правых прямоугольников (рис.7.4):
Рис. 7.4. Геометрическая интерпретация правых метода
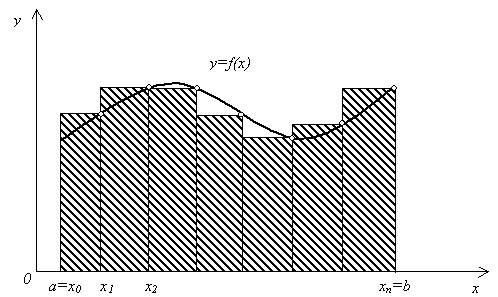
Более точной является формула прямоугольников, использующая функции в средних точках участков (рис.7.5):
Рис. 7.5. Иллюстрация метода средних прямоугольников
Метод трапеций Метод трапеций использует линейную интерполяцию, т.е. график функции
Рис. 7.6. Геометрическая интерпретация метода трапеций Площадь каждой такой трапеции равна произведению полусуммы оснований на высоту. Складывая эти равенства, получим следующую формулу для вычислений:
Точность интегрирования зависит от степени многочлена, количества участков и расположение точек. Во многих случаях формула средних прямоугольников дает лучшую точность, чем формула трапеций. Это на первый взгляд неожиданно, так как формула прямоугольников использует интерполяцию нулевого порядка, а формула трапеций – нелинейную. Здесь все дело в особом рассположении точек, которое повышает точность. 7.3. Метод парабол (Симпсона) Метод парабол (Симпсона) подразумевает разбиение отрезка интегрирования На каждом участке строится парабола, находится площадь фигуры, ограниченной полиномом 2–й степени и графиком подынтегральной функции. Далее находится сумма этих площадей. В результате получим следующую формулу для вычислений:
Лабораторная работа 7
|
||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 514; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |

 на отрезке интегрирования:
на отрезке интегрирования:
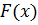 через элементарные функции.
через элементарные функции. вычисляется через элементарную функцию, но выражение довольно сложное для вычисления.
вычисляется через элементарную функцию, но выражение довольно сложное для вычисления.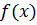 выражена таблицей.
выражена таблицей.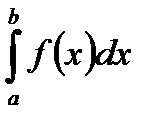
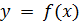 , осью абсцисс и прямыми
, осью абсцисс и прямыми 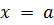 и
и 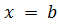 .
.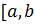 ] на
] на 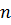 равных частей длиной
равных частей длиной  так что
так что 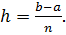 При этом получим точки (рис.7.1).
При этом получим точки (рис.7.1).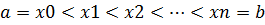 ;
;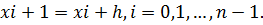

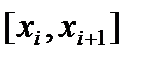 длины
длины 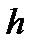 , тогда получим квадратурные формулы.
, тогда получим квадратурные формулы.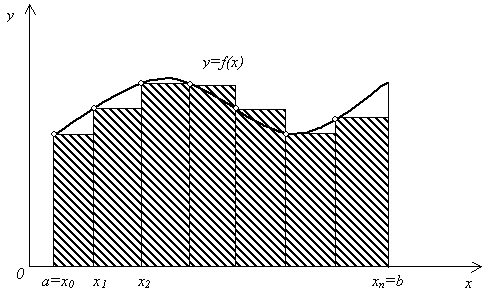
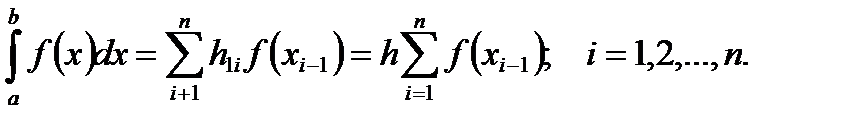


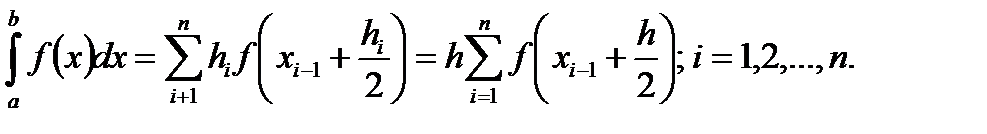
 представляется в виде ломаной, соединяющей точки
представляется в виде ломаной, соединяющей точки 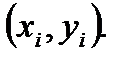 В этом случае площадь всей фигуры складывается из площадей элементарных трапеций (рис. 7.6):
В этом случае площадь всей фигуры складывается из площадей элементарных трапеций (рис. 7.6):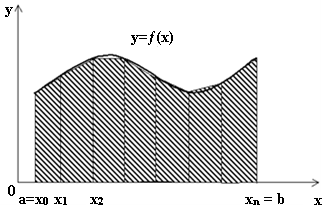
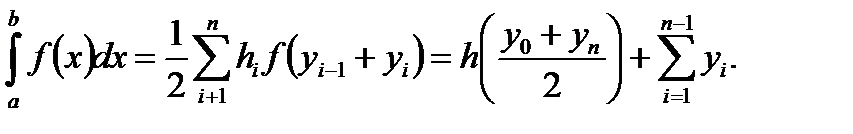
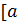 ,
,  на четное число
на четное число  равных частей с шагом
равных частей с шагом 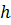 . На каждом отрезке подынтегральную функцию заменяют многочленом второй степени, т.е. уравнением квадратичной параболы.
. На каждом отрезке подынтегральную функцию заменяют многочленом второй степени, т.е. уравнением квадратичной параболы.



