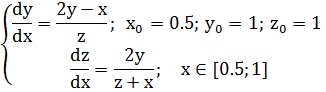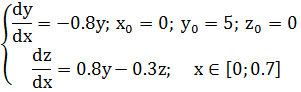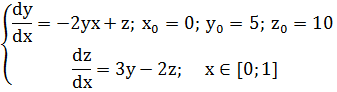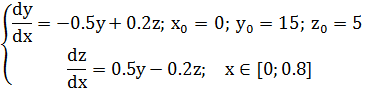Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сравнение методов решения дифференциального управленияСодержание книги
Поиск на нашем сайте Сравним время решения ДУ по каждому из методов. Если мы уменьшим шаг Оба метода являются одношаговыми. Особенность таких методов состоит в том, что для получения решения в каждом новом расчетном узле достаточно иметь значение сеточной функции лишь в предыдущем узле. Это позволяет непосредственно начать счет при Лабораторная работа 8 Решение обыкновенных дифференциальных уравнений Цель работы: изучить методы Эйлера и Рунге-Кутта для решения обыкновенных дифференциальных уравнений и системы ОДУ, формулы для вычисления, написать программу на языке программирования для реализации данных методов. Алгоритм метода Эйлера:
Ввод
Начало цикла, условие
Печать Конец цикла. Алгоритм метода Эйлера для системы уравнений:
Начальное условие: при Ввод
Начало цикла, условие
Печать Конец цикла. Варианты заданий Задание № 1. Численное решение задачи Коши для обыкновенных дифференциальных уравнений. Вариант 1. Решить дифференциальное уравнение Вариант 2. Решить дифференциальное уравнение Вариант 3. Решить дифференциальное уравнение Вариант 4. Решить дифференциальное уравнение Вариант 5. Решить дифференциальное уравнение Вариант 6. Решить дифференциальное уравнение Вариант 7. Решить дифференциальное уравнение Вариант 8. Решить дифференциальное уравнение Вариант 9. Решить дифференциальное уравнение Вариант 10. Решить дифференциальное уравнение Задание № 2. Численное решение систем обыкновенных дифференциальных уравнений. Вариант 1. Решить систему обыкновенных дифференциальных уравнений с шагом интегрирования
Вариант 2. Решить систему обыкновенных дифференциальных уравнений с шагом интегрирования
Вариант 3. Решить систему обыкновенных дифференциальных уравнений с шагом интегрирования
Вариант 4. Решить систему обыкновенных дифференциальных уравнений с шагом интегрирования
Вариант 5. Решить систему обыкновенных дифференциальных уравнений с шагом интегрирования
Вариант 6. Решить систему обыкновенных дифференциальных уравнений с шагом интегрирования
Вариант 7. Решить систему обыкновенных дифференциальных уравнений с шагом интегрирования
Вариант 8. Решить систему обыкновенных дифференциальных уравнений с шагом интегрирования
Вариант 9. Решить систему обыкновенных дифференциальных уравнений с шагом интегрирования
Вариант 10. Решить систему обыкновенных дифферен-циальных уравнений с шагом интегрирования
|
||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 124; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

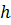 в два раза, то, поскольку метод Рунге–Кутта имеет порядок точности
в два раза, то, поскольку метод Рунге–Кутта имеет порядок точности  погрешность уменьшится в 16 раз. Поскольку на каждом шаге правая часть уравнения вычисляется 4 раза, то количество вычислений увеличится в 8 раз. Чтобы уменьшить погрешность вычислений по методу Эйлера в 16 раз, необходимо уменьшить шаг в 16 раз, это значит, что в столько же раз увеличится количество вычислений правой части. Значит, для метода Рунге-Кутта потребуется в два раза меньше времени вычислений. Кроме того, при вычислении с шагом
погрешность уменьшится в 16 раз. Поскольку на каждом шаге правая часть уравнения вычисляется 4 раза, то количество вычислений увеличится в 8 раз. Чтобы уменьшить погрешность вычислений по методу Эйлера в 16 раз, необходимо уменьшить шаг в 16 раз, это значит, что в столько же раз увеличится количество вычислений правой части. Значит, для метода Рунге-Кутта потребуется в два раза меньше времени вычислений. Кроме того, при вычислении с шагом  по известным начальным значениям, что допускает изменение шага в любой точке в процессе расчета. Недостатком одношаговых методов является трудность выбора шага.
по известным начальным значениям, что допускает изменение шага в любой точке в процессе расчета. Недостатком одношаговых методов является трудность выбора шага.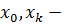 концы интервала;
концы интервала; шаг интегрирования;
шаг интегрирования;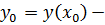 начальное условие;
начальное условие;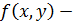 правая часть уравнения.
правая часть уравнения.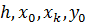 ;
; ;
;

 ;
;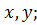
 ;
; ;
;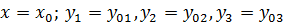 ;
; ;
; ;
; ;
;
 при начальных условиях
при начальных условиях  с шагом интегрирования
с шагом интегрирования  на интервале
на интервале  .
. при начальных условиях
при начальных условиях  с шагом интегрирования
с шагом интегрирования 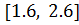 .
.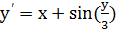 при начальных условиях
при начальных условиях  .
. при начальных условиях
при начальных условиях 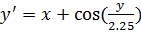 при начальных условиях
при начальных условиях 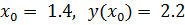 с шагом интегрирования
с шагом интегрирования  на интервале
на интервале  ].
].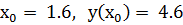 с шагом интегрирования
с шагом интегрирования  при начальных условиях
при начальных условиях  с шагом интегрирования
с шагом интегрирования  .
.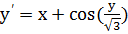 при начальных условиях
при начальных условиях 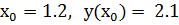 с шагом интегрирования
с шагом интегрирования  .
. при начальных условиях
при начальных условиях 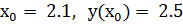 с шагом интегрирования
с шагом интегрирования 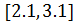 .
.