
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифракция Фраунгофера на одной щелиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Дифракция Фраунгофера (или дифракция плоских световых волн, или дифракция в параллельных лучах) наблюдается в том случае, когда источник света и точка наблюдения бесконечно удалены от препятствия, вызвавшего дифракцию. Для наблюдения дифракции Фраунгофера необходимо точечный источник поместить в фокусе собирающей линзы, а дифракционную картину можно исследовать в фокальной плоскости второй собирающей линзы, установленной за препятствием (рис.10). Пусть монохроматическая волна падает нормально плоскости бесконечно длинной узкой щели ( Разобьём волновую поверхность на участке щели МN на зоны Френеля, имеющие вид полос, параллельных ребру М щели. Ширина каждой полосы выбирается так, чтобы разность хода от краев этих зон была равна Число зон Френеля
Рис.10. Дифракция Фраунгофера на одной щели Условие минимума при дифракции Френеля: Если число зон Френеля четное:
или
то в точке Р наблюдается дифракционный минимум. Условие максимума: Если число зон Френеля нечетное
то наблюдается дифракционный максимум. При Основная часть световой энергии сосредоточена в главном максимуме: Сужение щели приводит к уширению главного максимума и уменьшению его яркости (то же и с другими максимумами). При уширении щели ( При падении белого света будет разложение на его составляющие. При этом фиолетовый свет будет отклоняться меньше, синий - больше и т.д., красный - максимально. Главный максимум в этой случае будет белого цвета. Дифракционная решетка Дифракционная решетка представляет собой совокупность большого числа
Рис .11. Дифракционная решетка ( Расстояние
Дифракционная картина на решетке определяется как результат взаимной интерференции волн, идущих от всех щелей, т.е. в дифракционной решетке осуществляется многолучевая интерференция. Так как щели находятся друг от друга на одинаковых расстояниях, то разности хода лучей, идущих от двух соседних щелей, будут для данного направления
В направлениях, в которых наблюдается минимум для одной щели, будут минимумы и в случае
Условие максимумов: те случаи Условие главных максимумов:
где Эти максимумы будут расположены симметрично относительно центрального (нулевого Для тех углов Условие дополнительных максимумов:
Между главными максимума будут располагаться ( Условие дополнительных минимумов:
На рассмотренные максимумы и минимумы накладываются минимумы, возникающие при дифракции от отдельной щели. График распределения интенсивности света вдоль экрана от решетки приведен на рис. 12. Данный рисунок выполнен для случая решетки, состоящей из четырех щелей (
Рис. 12. Распределение интенсивности при дифракции Фраунгофера на дифракционной решетке Пунктирная кривая, проходящая через вершины главных максимумов изображает интенсивность от одной щели, умноженную на Добавочные максимумы слабы по сравнению с главными максимумами. При большом числе щелей они почти не видны. Добавочные максимумы создают слабый фон, на котором выступают резкие главные максимумы, в которых концентрируется практически весь дифрагированный свет. Дифракционная картина, при дифракции на дифракционной решетке зависит от Пусть Наблюдая в монохроматическом свете дифракционные картины от решетки, можно определить длину световой волны
|
||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 411; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.211.135 (0.008 с.) |

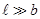 ),
), 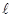 - длина,
- длина, 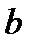 - ширина. Разность хода между лучами 1 и 2 в направлении
- ширина. Разность хода между лучами 1 и 2 в направлении 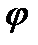 :
: 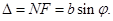 (10).
(10).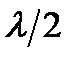 , т.е. всего на ширине щели уложится
, т.е. всего на ширине щели уложится 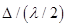 зон. Так как свет на щель падает нормально, то плоскость щели совпадает с фронтом волны, следовательно, все точки фронта в плоскости щели будут колебаться синфазно. Амплитуды вторичных волн в плоскости щели будут равны, так как выбранные зоны Френеля имеют одинаковые площади и одинаково наклонены к направлению наблюдения.
зон. Так как свет на щель падает нормально, то плоскость щели совпадает с фронтом волны, следовательно, все точки фронта в плоскости щели будут колебаться синфазно. Амплитуды вторичных волн в плоскости щели будут равны, так как выбранные зоны Френеля имеют одинаковые площади и одинаково наклонены к направлению наблюдения.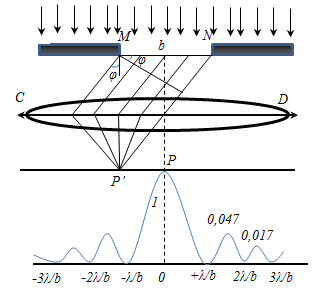
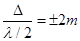 (11)
(11)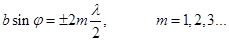 (12)
(12)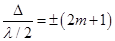 (13)
(13)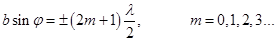 (14)
(14) = 0 в щели укладывается одна зона Френеля и, следовательно, в точке Р наблюдается главный (центральный) максимум нулевого порядка.
= 0 в щели укладывается одна зона Френеля и, следовательно, в точке Р наблюдается главный (центральный) максимум нулевого порядка.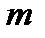 =0:1:2:3...;
=0:1:2:3...; 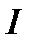 =1: 0,047: 0,017: 0,0083... (
=1: 0,047: 0,017: 0,0083... (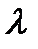 ) максимумы будут ярче, но дифракционные полосы становятся уже, а числе самих полос - больше. При
) максимумы будут ярче, но дифракционные полосы становятся уже, а числе самих полос - больше. При 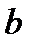 >>
>> 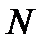 одинаковых по ширине и параллельных друг другу щелей, разделенных непрозрачными промежутками, также одинаковыми по ширине (рис.11).
одинаковых по ширине и параллельных друг другу щелей, разделенных непрозрачными промежутками, также одинаковыми по ширине (рис.11).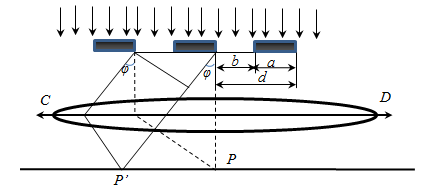
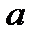 - ширина непрозрачного участка)
- ширина непрозрачного участка)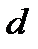 между соответственными точками соседних щелей называют периодом или постоянной решетки:
между соответственными точками соседних щелей называют периодом или постоянной решетки: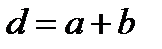 (15)
(15)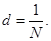 (16)
(16)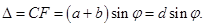 (17)
(17)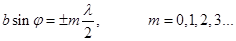 (18) - условие главных минимумов.
(18) - условие главных минимумов.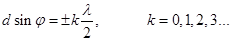 (19)
(19)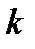 – порядок максимума
– порядок максимума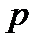 ,
, 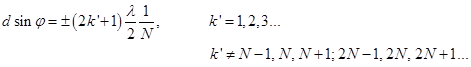 (20)
(20)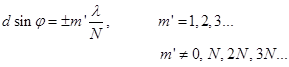 (21)
(21)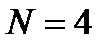 ) и
) и 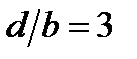 (
(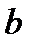 -ширина щели,
-ширина щели, 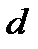 -период решетки).
-период решетки).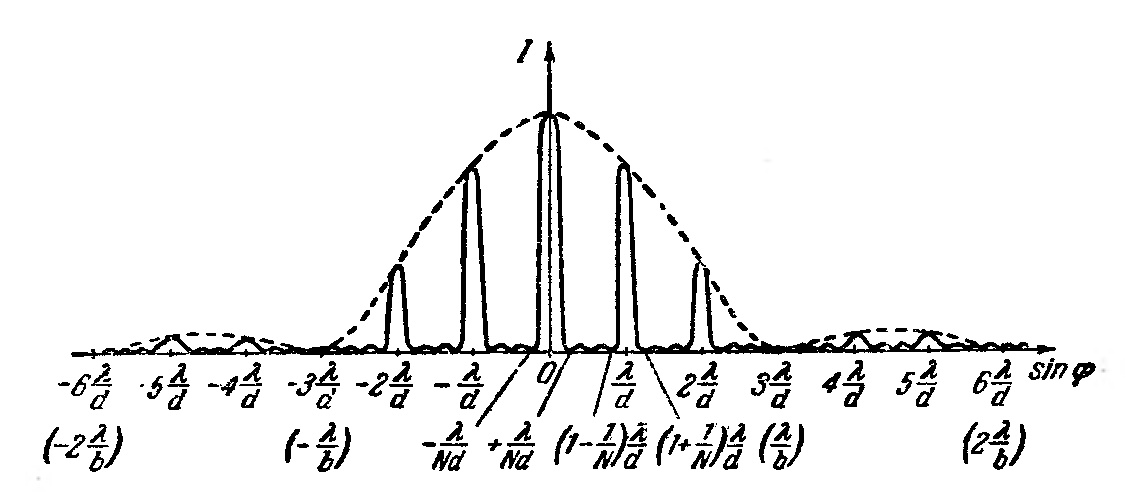
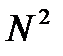 . При взятом отношении периода решетки к ширине щели (
. При взятом отношении периода решетки к ширине щели (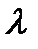 . Между ними по
. Между ними по 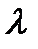 , так как направления, в которых наблюдаются дифракционные максимумы и минимумы, зависят от
, так как направления, в которых наблюдаются дифракционные максимумы и минимумы, зависят от 


