
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифракция Френеля на круглом отверстииСодержание книги
Поиск на нашем сайте
Пусть на пути сферической световой волны, испускаемой источником S, расположен непрозрачный экран с круглым отверстием радиуса Если отверстие открывает четное число зон Френеля, то в точке P будет наблюдаться минимум, так как все открытые зоны можно объединить в соседние пары, колебания которых в точке P приблизительно гасят друг друга. При нечетном числе зон в точке P будет максимум, так как колебания одной зоны останутся не погашенными.
Рис.7. Дифракция Френеля на круглом отверстии Можно показать, что радиус зоны Френеля с номером
Расстояние Если отверстие оставляет открытым целое число зон Френеля, то, приравняв
При
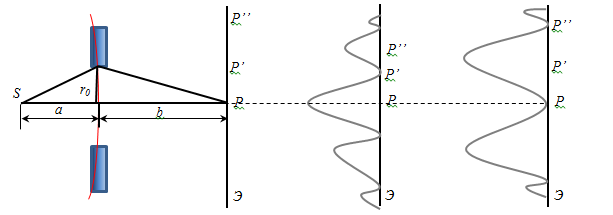
Рис.8. Распределение интенсивностей при дифракции Френеля на круглом отверстии Таким образом, дифракционная картина от круглого отверстия имеет вид чередующихся светлых и темных колец, причем к центре будет светлое пятно (максимум), если в отверстии укладывается нечетное число зон Френеля, либо темное, если укладывается четное число зон Френеля. Если Если Дифракция Френеля на диске Пусть диск закрывает следовательно,
Рис.9. Дифракция Френеля на диске Если Если Перемещение экрана вдоль линии SР не меняет картину на экране.
|
||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 212; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.119.191 (0.007 с.) |

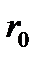 ( рис.7 ).
( рис.7 ).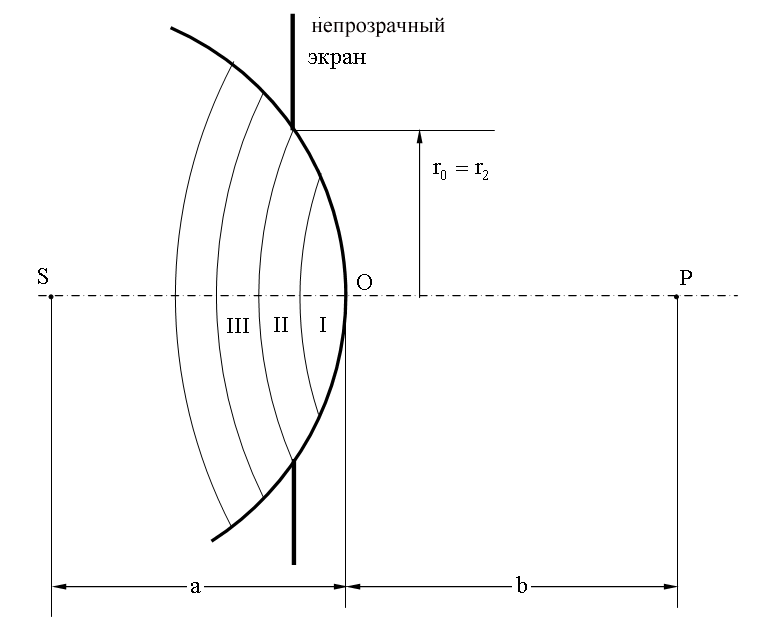
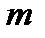 при не очень больших
при не очень больших 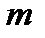 :
: 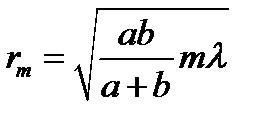 (7)
(7)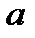 примерно равно расстоянию от источника до преграды, расстояние
примерно равно расстоянию от источника до преграды, расстояние 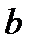 – от преграды до точки наблюдения P.
– от преграды до точки наблюдения P.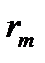 , получим формулу для подсчета числа открытых зон Френеля:
, получим формулу для подсчета числа открытых зон Френеля: 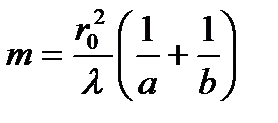 (8)
(8)
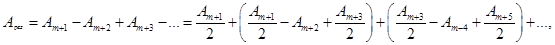 (9)
(9)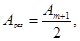 т.е. в точке Р наблюдается интерференционный максимум (светлое пятно). Если сместиться по экрану в точку Рʹ, то закроется часть (m+1)-й зоны, но откроется часть (m+2)-й зоны. Следовательно, в т. Рʹ будет минимум (темное кольцо). При смещении в точку Рʹʹ перекроется часть (m+2)-й зоны и одновременно откроется часть (m+3)-й зоны, следовательно, в точке Рʹʹ будет максимум. Таким образом, дифракционная картина на круглом диске имеет вид чередующихся светлых и темных концентрических колец. В центре картины всегда помещается светлое пятно.
т.е. в точке Р наблюдается интерференционный максимум (светлое пятно). Если сместиться по экрану в точку Рʹ, то закроется часть (m+1)-й зоны, но откроется часть (m+2)-й зоны. Следовательно, в т. Рʹ будет минимум (темное кольцо). При смещении в точку Рʹʹ перекроется часть (m+2)-й зоны и одновременно откроется часть (m+3)-й зоны, следовательно, в точке Рʹʹ будет максимум. Таким образом, дифракционная картина на круглом диске имеет вид чередующихся светлых и темных концентрических колец. В центре картины всегда помещается светлое пятно.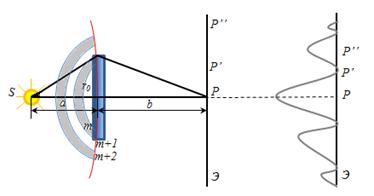
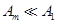 .
.


