
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 1. Основные т е оретические сведенияСодержание книги
Поиск на нашем сайте
МИНОБРНАУКИ РОССИИ Федеральное государственное бюджетное образовательное учреждение высшего образования ОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ Им. Ф.М. ДОСТОЕВСКОГО ДИФРАКЦИЯ СВЕТА Учебно-методическое пособие по курсам «Оптика» и «Общий физический практикум» Омск 2019 Рецензенты: К.ф.-м.н. Н.А. Давлеткильдеев (КНИОРП ОНЦ СО РАН) К.ф.-м.н., Г.М. Серопян ФГБОУ ВО ОмГУ им. Ф.М. Достоевского)
Дифракция света: учебно-методическое пособие по курсам «Оптика и «Общий физический практикум»/ авт.: Б.Т. Байсова, Л.В. Баранова.– Омск: изд-во Ом.гос.ун-та, 2019.–38 с.
В пособии представлены краткие теоретические сведения по разделу волновой оптики «Дифракция света», обеспечивающие выполнение цикла лабораторных работ. Пособие также включает в себя лабораторный практикум и представляет собой самостоятельное руководство к лабораторным занятиям для студентов физического факультета. Практикум содержит описание выполнения трех лабораторных работ по курсам «Оптика» и «Общий физический практикум». Предназначено для обучающихся по направлениям подготовки бакалавров 03.03.02 «Физика», 03.03.03 «Радиофизика».
ОГЛАВЛЕНИЕ ПРЕДИСЛОВИЕ……………………………………………………………………5 ГЛАВА 1. Основные теоретические сведения……………………...…………..6 1.1. Дифракция света……………………………………………………..…….…6 1.2. Дифракционные картины от различных препятствий…………...…………7 1.3. Принцип Гюйгенса-Френеля……………………………………………...….8 1.3.1. Математическая формулировка принципа Гюйгенса-Френеля…………………………………………………………………9 1.4. Зоны Френеля…………………………………………………..…………....10 1.4.1. Определение положений максимумов и минимумов методом зон Френеля..................................................................................................11 1.4.2. Дифракция Френеля на круглом отверстии……………..…….……12 1.5. Дифракция Френеля на диске………………………………..…….………13 1.6. Дифракция Фраунгофера на одной щели…………………..…………..…14 1.7. Дифракционная решетка……………………………………………….…..16 1.8. Дифракционная решетка как спектральный прибор……………………..18 1.9. Критерий Рэлея……………………………………………………………..20 1.10. Дифракция на пространственной решетке. Формула Вульфа-Брэггов…21 1.11. Рассеяние света. Закон Релея………………………………………………22 ГЛАВА 2. Лабораторный практикум…………..……………………………....24 2.1. Изучение дифракции Фраунгофера от щели и дифракционной решетки……………………………………………………………………………...24 2.2. Определение периода и угловой дисперсии дифракционных решеток….28 2.3. Исследование дифракции Френеля на круглом отверстии………….……32 СПИСОК ИСПОЛЬЗОВАННОЙ И РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ………………………………………………..………………..…38 ПРЕДИСЛОВИЕ Целью настоящего учебно-методического пособия является ознакомление студентов с основными теоретическими сведениями по теме «Дифракция света» с последующим закреплением теории на практике при выполнении цикла лабораторных работ. Пособие способствует формированию у студентов практических навыков работы на оптическом оборудовании с возможностью наглядного наблюдения изучаемых явлений с последующим оформлением результатов эксперимента. В первой главе изложены краткие теоретические сведения. В представленном теоретическом материале рассмотрены основные условия наблюдения дифракции света, описана дифракция Френеля (на круглом отверстии и на диске) и дифракция Фраунгофера (на щели и дифракционной решетке), расчет дифракционной картины с помощью принципа Гюйгенса-Френеля, а также описаны характеристики дифракционной решетки как спектрального прибора. Во второй главе представлен лабораторный практикум, включающий три работы: «Изучение дифракции Фраунгофера от щели и дифракционной решетки», «Определение периода и угловой дисперсии дифракционных решеток», «Исследование дифракции Френеля на круглом отверстии». По каждой работе представлены методические указания о порядке ее выполнения, описание лабораторных установок, а также перечень контрольных вопросов и список рекомендуемой литературы. Дифракция света При распространении электромагнитной волны в однородной среде геометрическая форма фронта волны не испытывает изменения. Если же волна распространяется в неоднородной среде или на пути световой волны находятся непрозрачные тела или экраны с отверстиями, то за этими телами образуется область тени. Эту область можно очертить геометрически, зная, что свет распространяется прямолинейно и световые лучи есть прямые линии. Наблюдение показывает, что световые волны заходят в область геометрической тени, причём на границе между областями света и тени появляются чередующиеся максимумы и минимумы света, свидетельствующие о некотором перераспределении световой энергии на этой границе. Это явление огибания световыми волнами границ непрозрачных тел с образованием интерференционного перераспределения энергии по различным направлениям называется дифракцией (от лат. difractus - преломленный).
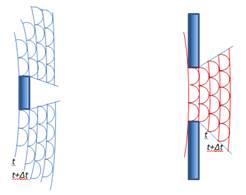
Рис.1. Огибание волнами препятствий.
Под дифракцией понимается любое отклонение света от прямолинейного распространения, если только оно не может быть объяснено как отражение, преломление или изгибание лучей в оптически неоднородных средах. Дифракция наблюдается всегда, когда изменение амплитуды или фазы волны неодинаково по всей поверхности волнового фронта. Дифракция света определяет границы применимости геометрической оптики. Если
Принцип Гюйгенса-Френеля Первая теория дифракции света, количественно описывавшая явление, предложена французским физиком Френелем. В основе теории лежит принцип Гюйгенса-Френеля. Гюйгенс, изучавший закономерности направления распространения волн, предположил, что каждую точку волнового фронта можно считать центром вторичных сферических волн, а волновой фронт в любой последующий момент времени – огибающей этих волн. Френель дополнил принцип Гюйгенса утверждением, что вторичные волны интерферируют между собой. Благодаря этому огибающая вторичных волн, введенная Гюйгенсом формально, приобрела физическое содержание как поверхность, где, благодаря взаимной интерференции вторичных волн, которые когерентны, результирующая волна имеет максимальную интенсивность. Итак, принцип Гюйгенса-Френеля: 1. Каждая точка волновой поверхности, которой достигла в данный момент волна, является центром элементарных вторичных волн,их внешняя огибающая будет волновой поверхностью в последующий момент времени (рис.3); S1 и S2 - волновые поверхности соответственно в моменты t1 и t2; t2 > t1). (Х. Гюйгенс, 1678 г.).
Рис. 3. Источники вторичных волн 2. Амплитуда результирующей волны в любой точке пространства может быть найдена как результат интерференции всех вторичных волн, с учетом их фаз и амплитуд (О. Френель, 1818 г.). Для того чтобы определить результат дифракции в некоторой точке пространства, следует рассчитать, согласно принципу Гюйгенса-Френеля, интерференцию вторичных волн, попавших в эту точку от волновой поверхности. Для волновой поверхности произвольной формы такой расчет достаточно сложен, но в отдельных случаях (сферическая или плоская волновая поверхность, симметричное расположение точки относительно волновой поверхности и непрозрачной преграды) вычисления сравнительно просты. Волновую поверхность при этом разбивают на отдельные участки (зоны Френеля), расположенные определенным образом, что упрощает математические операции.
Зоны Френеля
Вычисление интеграла по формуле (3) в общем случае затруднительно. Френель решил задачу нахождения амплитуды в т. Р, заменив интегрирование суммированием, т.е. перешёл от непрерывных сумм ( В случаях, если в задаче существует симметрия, амплитуду результирующего колебания можно найти методом зон Френеля, не прибегая к вычислению интеграла. Пусть от источника света S (рис. 5) распространяется монохроматическая сферическая волна, P –точка наблюдения.
Рис.5.Зоны Френеля
Через точку O проходит сферическая волновая поверхность. Она симметрична относительно прямой SP. Разобьем эту поверхность на кольцевые зоны I, II, III и т.д. так, чтобы расстояния от краев зоны до точки P отличались на Возьмем произвольную точку 1 в первой зоне Френеля. В зоне II найдется, в силу правила построения зон, такая соответствующая ей точка, что разность хода лучей, идущих в точку P от точек 1 и 2 будет равна Из геометрических соображений следует, что при не очень больших номерах зон их площади примерно одинаковы. Значит, каждой точке первой зоны найдется соответствующая ей точка во второй, колебания которых погасят друг друга. Амплитуда результирующего колебания, приходящего в точку P от зоны с номером Происходит это из-за увеличения с ростом
Дифракция Френеля на диске Пусть диск закрывает следовательно,
Рис.9. Дифракция Френеля на диске Если Если Перемещение экрана вдоль линии SР не меняет картину на экране. Дифракционная решетка Дифракционная решетка представляет собой совокупность большого числа
Рис .11. Дифракционная решетка ( Расстояние
Дифракционная картина на решетке определяется как результат взаимной интерференции волн, идущих от всех щелей, т.е. в дифракционной решетке осуществляется многолучевая интерференция. Так как щели находятся друг от друга на одинаковых расстояниях, то разности хода лучей, идущих от двух соседних щелей, будут для данного направления
В направлениях, в которых наблюдается минимум для одной щели, будут минимумы и в случае
Условие максимумов: те случаи Условие главных максимумов:
где Эти максимумы будут расположены симметрично относительно центрального (нулевого Для тех углов Условие дополнительных максимумов:
Между главными максимума будут располагаться ( Условие дополнительных минимумов:
На рассмотренные максимумы и минимумы накладываются минимумы, возникающие при дифракции от отдельной щели. График распределения интенсивности света вдоль экрана от решетки приведен на рис. 12. Данный рисунок выполнен для случая решетки, состоящей из четырех щелей (
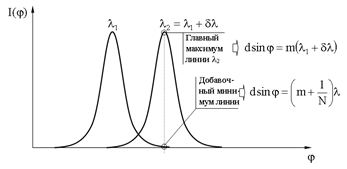
Рис. 12. Распределение интенсивности при дифракции Фраунгофера на дифракционной решетке Пунктирная кривая, проходящая через вершины главных максимумов изображает интенсивность от одной щели, умноженную на Добавочные максимумы слабы по сравнению с главными максимумами. При большом числе щелей они почти не видны. Добавочные максимумы создают слабый фон, на котором выступают резкие главные максимумы, в которых концентрируется практически весь дифрагированный свет. Дифракционная картина, при дифракции на дифракционной решетке зависит от Пусть Наблюдая в монохроматическом свете дифракционные картины от решетки, можно определить длину световой волны
Угловая дисперсия Одной из главных характеристик спектрального прибора является угловая дисперсия. По определению, угловой дисперсией
Здесь и далее В определении угловой дисперсии
Угловая дисперсия принимает только положительные значения. Угловая дисперсия тем больше, чем меньше период решетки, она растет с ростом порядка максимума. Угловая дисперсия одинакова в максимумах с порядками
Рис. 13. К определению угловой дисперсии Критерий Релея Критерий Релея определяет величину
По определению разрешающая сила:
Рис. 14.Критерий Релея Разрешающая сила R есть величина, обратная относительной погрешности определения длины волны. Она показывает, во сколько раз длина волны Подчеркнем, что
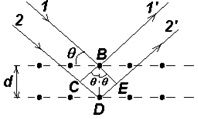
Рис.15. Поперечные размеры пучка и решетки Если же Кроме того, предполагается, что колебания от всех Формула Вульфа — Брэггов Для наблюдения дифракционной картины необходимо, чтобы постоянная решетки была того же порядка, что и длина волны падающего излучения. Кристаллы, являясь трехмерными пространственными решетками, имеют постоянную порядка 10-10м и, следовательно, непригодны для наблюдения дифракции в видимом свете (~=5·10-7м). Эти факты позволили немецкому физику М. Лауэ (1879—1960 гг.) прийти к выводу, что в качестве естественных дифракционных решеток для рентгеновского излучения можно использовать кристаллы, поскольку расстояние между атомами в кристаллах одного порядка с рентгеновского излучения (10-12―10-8м). Простой метод расчета дифракции рентгеновского излучения от кристаллической решетки предложен независимо друг от друга советским физиком Г. В. Вульфом (1863—1925 гг.) и английскими физиками Г. и Л. Брэггами (отец (1862—1942гг.) и сын (1890—1971гг.)). Они предположили, что дифракция рентгеновских лучей является результатом их отражения от системы параллельных кристаллографических плоскостей (плоскостей, в которых лежат узлы (атомы) кристаллической решетки). Представим кристаллы в виде совокупности параллельных кристаллографических плоскостей (рис. 27), отстоящих друг от друга на расстоянии
Рис.16. Дифракция рентгеновских лучей Пучок параллельных монохроматических рентгеновских лучей (1, 2) падает под углом скольжения (угол между направлением падающих лучей и кристаллографической плоскостью) и возбуждает атомы кристаллической решетки, которые становятся источниками когерентных вторичных волн 1'и 2', интерферирующих между собой, подобно вторичным волнам, от щелей дифракционной решетки. Максимумы интенсивности (дифракционные максимумы) наблюдаются в тех направлениях, в которых все отраженные атомными плоскостями волны будут находиться в одинаковой фазе. Эти направления удовлетворяют формуле Вульфа – Брэггов:
т. е. при разности хода между двумя лучами, отраженными от соседних кристаллографических плоскостей, кратной целому числу длин волн, наблюдается дифракционный максимум. При произвольном направлении падения монохроматического рентгеновского излучения на кристалл дифракция не возникает. Чтобы ее наблюдать, надо, поворачивая кристалл, найти угол скольжения. Дифракционная картина может быть получена и при произвольном положении кристалла, для чего нужно пользоваться непрерывным рентгеновским спектром, испускаемым рентгеновской трубкой. Тогда для таких условий опыта всегда найдутся длины волн, удовлетворяющие условию (32). Порядок выполнения работы В настоящей работе в качестве источника света используется лазер, дающий монохроматическую световую волну. Устройство гониометра Измерения углов дифракции Гониометр (рис. 1) состоит из зрительной 1 и коллиматорной 2 труб и предметного столика 3. Коллиматорная труба имеет раздвижную щель 4, которая освещается источником света, в данной работе ртутной лампой. Коллиматорная труба неподвижна. Зрительная труба крепится на алидаде 5. Алидаду можно вращать, если отпущен зажимной винт 6. Если винт 6 закреплен, алидаду можно вращать с помощью микрометреннного винта 7. Столик может вращаться вместе с алидадой, если закреплен зажимной винт 8. При отпущенном винте 8 столик можно вращать рукой относительно алидады.
Рис. 1. Внешний вид гониометра Четкость границ изображения щели добивается вращением винта 12, расположенного на зрительной трубе. Измерения рекомендуется проводить в темноте. Порядок выполнения работы 1. Включите ртутную лампу, а затем подсветку гониометра. Вращая алидаду, наведите на щель коллиматора вертикальную нить креста, имеющегося в поле зрения зрительной трубы. Закрепите алидаду в этом положении. 2. Поставьте на столик первую дифракционную решетку так, чтобы ее щели (штрихи) были вертикальны. Снимите отчет Отчет снимается по шкале, рассматриваемой через отчетный микроскоп 10 (рис.1). Подсветка шкалы включается тумблером, расположенным на гониометре. Поле зрения окуляра отчетного микроскопа приведено на рис. 2. В поле зрения отчетного микроскопа виден лимб (круговая шкала) и вертикальная шкала, расположена справа от лимба. Рис. 2. Поле зрения окуляра отчетного микроскопа Для того, чтобы снять отчет, необходимо повернуть маховичок 11 (см. рис.1) настолько, чтобы верхние и нижние штрихи в левом окне точно совместились. Число градусов будет равно видимому ближайшему слева от риски прямому числу (число на верхней шкале лимба). На рис. 2 это число 7°. Число десятков минут равно числу интервалов, заключенных между верхним штрихом, который соответствует числу градусов, и нижним оцифрованным штрихом, отличающимся от верхнего на 180°. На рис. 2 это 5 интервалов между штрихами, оцифрованными прямым числом 7 на верхней шкале лимба, и двойными штрихами, оцифрованными перевернутым числом 187°, на нижней шкале. Число десятков минут равно пяти, каждый по 10', т.е. 50'. Число единиц минут отчитывается по шкале в правом окне по левому ряду чисел. Число минут это цифра над отчетной горизонтальной риской А, находящейся в поле зрения (на рис. 2 это цифра 1). Число секунд отчитывается в том же окне по правому ряду чисел, относительно риски А (на рис. 2 положение горизонтальной риски А даёт 36''. Положение, показанное на рис. 2 соответствует отчету 7°51'36''. Отчет 3. Поверните зрительную трубу вправо и снимите отчеты 4. Вычислите углы дифракции Примечание. При вычислении углов дифракции предварительно необходимо углы Произведем, например, вычисление угла дифракции при Так как Полученные значения углов дифракции можно перевести в радианы, учитывая, что 180º=3,14 рад. В частности в нашем случае 5. По формуле
вычислите период решетки. Найдите среднее значение периода Примечание. Для получения периода решетки в мкм длины волн линий необходимо перевести в мкм, учитывая, что 1 нм=10-3 мкм. 6. Вычислите угловую дисперсию в спектрах 1-го и 2-го порядков по формуле:
где Примечание. Единицы измерения угловой дисперсии определяются тем, в каких единицах выражены значения углов и длин волн. В случае, если углы взяты в градусах, а длина волны в нанометрах (нм), то угловая дисперсия получается в угл.град/нм. Если же углы взяты в радианах, то угловая дисперсия получается в единицах рад/нм. Все описанные измерения выполните для второй решетки. Таблица 1. Дифракционная решетка №___
Контрольные вопросы 1. Какое явление называется дифракцией? 2. Сформулируйте принцип Гюйгенса-Френеля. 3. Как может быть учтено действие непрозрачных экранов с отверстиями, установленных на пути пучка света (выбор поверхности σ)? 4. Чем отличается дифракция Фраунгофера от дифракции Френеля? 5. Начертите график распределения интенсивности на экране при дифракции Фраунгофера от дифракционной решетки. 6. Запишите условие дифракционного минимума и максимума при дифракции Фраунгофера от дифракционной решетки. 7. Дайте определение угловой дисперсии спектрального прибора. 8. Получите формулу для угловой дисперсии дифракционной решетки. 9. Опишите порядок выполнения измерений.
Зоны Френеля В ряде случаев удобно в качестве поверхности На рис. 1 S – источник света; P – точка наблюдения; буквой B 1 P = B 2 P = B 3 P = ……………… где
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 190; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.01 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

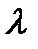 - длина волны,
- длина волны, 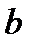 - размеры препятствия,
- размеры препятствия, 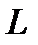 - расстояние от препятствия до точки наблюдения, то различают следующие ситуации:
- расстояние от препятствия до точки наблюдения, то различают следующие ситуации:  -геометрическая оптика
-геометрическая оптика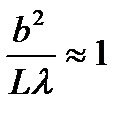 - дифракция Френеля (1)
- дифракция Френеля (1)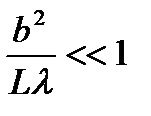 -дифракция Фраунгофера
-дифракция Фраунгофера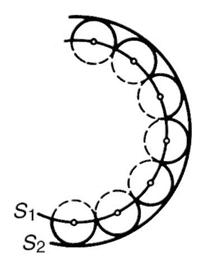
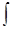 ) к дискретным (Σ).
) к дискретным (Σ).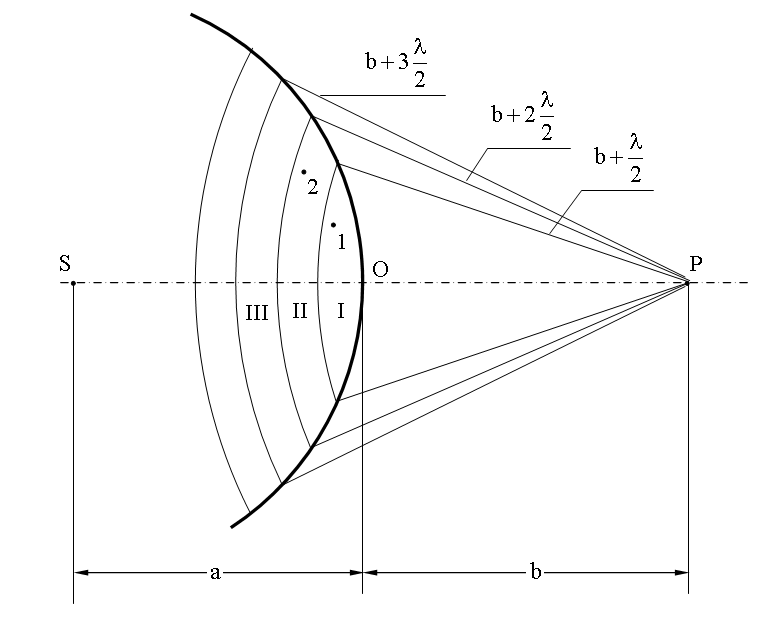
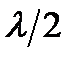 - половину длины световой волны. Построенные таким образом сектора сферы называются зонами Френеля.
- половину длины световой волны. Построенные таким образом сектора сферы называются зонами Френеля.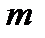 , уменьшается с ростом
, уменьшается с ростом 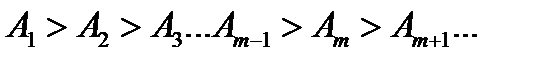
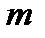 первых зон Френеля. Тогда амплитуда результирующего колебания в точке Р (рис.9).
первых зон Френеля. Тогда амплитуда результирующего колебания в точке Р (рис.9). 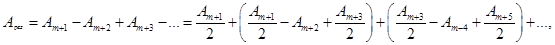 (9)
(9)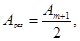 т.е. в точке Р наблюдается интерференционный максимум (светлое пятно). Если сместиться по экрану в точку Рʹ, то закроется часть (m+1)-й зоны, но откроется часть (m+2)-й зоны. Следовательно, в т. Рʹ будет минимум (темное кольцо). При смещении в точку Рʹʹ перекроется часть (m+2)-й зоны и одновременно откроется часть (m+3)-й зоны, следовательно, в точке Рʹʹ будет максимум. Таким образом, дифракционная картина на круглом диске имеет вид чередующихся светлых и темных концентрических колец. В центре картины всегда помещается светлое пятно.
т.е. в точке Р наблюдается интерференционный максимум (светлое пятно). Если сместиться по экрану в точку Рʹ, то закроется часть (m+1)-й зоны, но откроется часть (m+2)-й зоны. Следовательно, в т. Рʹ будет минимум (темное кольцо). При смещении в точку Рʹʹ перекроется часть (m+2)-й зоны и одновременно откроется часть (m+3)-й зоны, следовательно, в точке Рʹʹ будет максимум. Таким образом, дифракционная картина на круглом диске имеет вид чередующихся светлых и темных концентрических колец. В центре картины всегда помещается светлое пятно.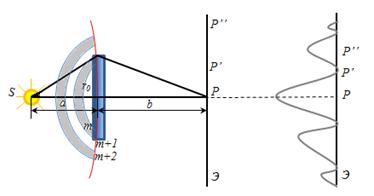
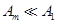 .
.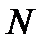 одинаковых по ширине и параллельных друг другу щелей, разделенных непрозрачными промежутками, также одинаковыми по ширине (рис.11).
одинаковых по ширине и параллельных друг другу щелей, разделенных непрозрачными промежутками, также одинаковыми по ширине (рис.11).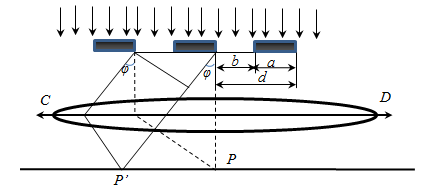
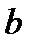 -ширина щели;
-ширина щели; 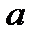 - ширина непрозрачного участка)
- ширина непрозрачного участка)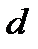 между соответственными точками соседних щелей называют периодом или постоянной решетки:
между соответственными точками соседних щелей называют периодом или постоянной решетки: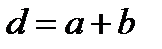 (15)
(15)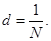 (16)
(16)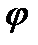 одинаковы в пределах всей дифракционной решетки:
одинаковы в пределах всей дифракционной решетки: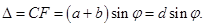 (17)
(17)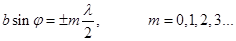 (18) - условие главных минимумов.
(18) - условие главных минимумов.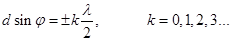 (19)
(19)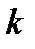 – порядок максимума
– порядок максимума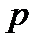 ,
, 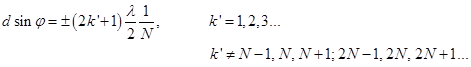 (20)
(20)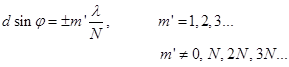 (21)
(21)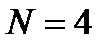 ) и
) и 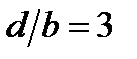 (
(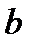 -ширина щели,
-ширина щели, 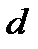 -период решетки).
-период решетки).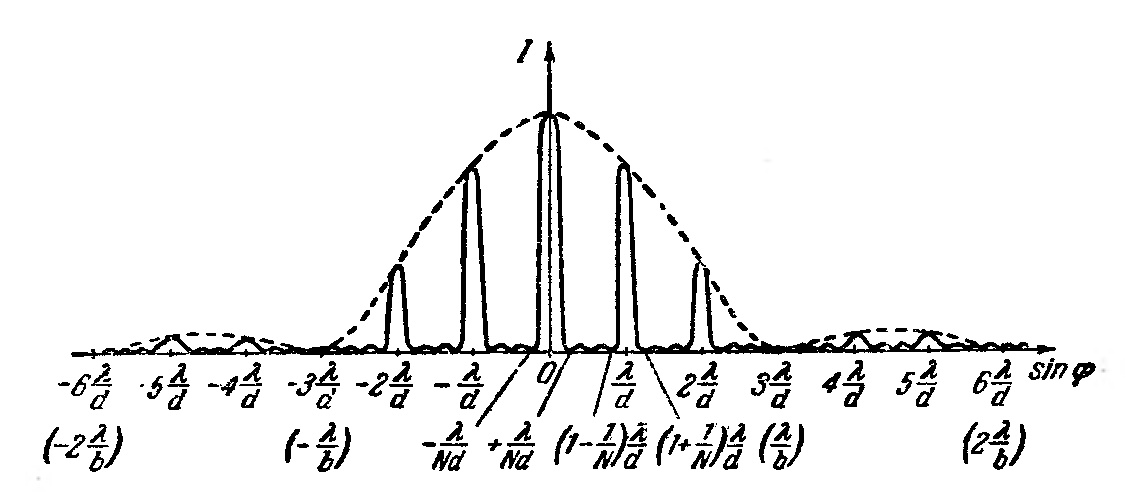
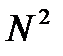 . При взятом отношении периода решетки к ширине щели (
. При взятом отношении периода решетки к ширине щели (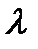 . Между ними по
. Между ними по 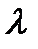 , так как направления, в которых наблюдаются дифракционные максимумы и минимумы, зависят от
, так как направления, в которых наблюдаются дифракционные максимумы и минимумы, зависят от 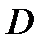 называется величина:
называется величина: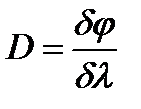 (22)
(22)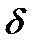 – знак дифференциала, так как буква
– знак дифференциала, так как буква 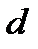 используется – она обозначает постоянную решетки.
используется – она обозначает постоянную решетки.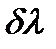 – разность длин волн двух соседних линий,
– разность длин волн двух соседних линий, 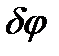 – соответствующая разность углов, под которыми наблюдаются главные максимумы. Выразим угловую дисперсию через постоянную решетки
– соответствующая разность углов, под которыми наблюдаются главные максимумы. Выразим угловую дисперсию через постоянную решетки 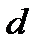 , порядок спектра
, порядок спектра 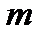 и угол
и угол 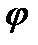 , под которым наблюдается максимум. Для этого найдем дифференциал от правой и левой части условия главного максимума:
, под которым наблюдается максимум. Для этого найдем дифференциал от правой и левой части условия главного максимума: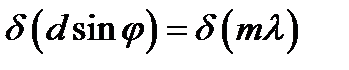 , (23)
, (23)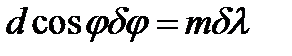 , (24)
, (24)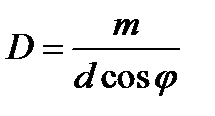 (25)
(25)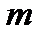 и
и 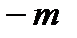 . При малых
. При малых 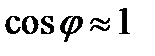 и
и 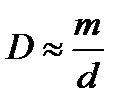 .
.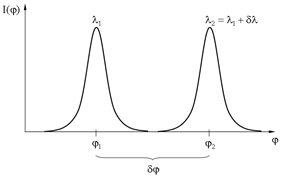
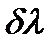 в соответствии с рис.14. Считают, что линии разрешены, если главный максимум линии
в соответствии с рис.14. Считают, что линии разрешены, если главный максимум линии 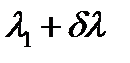 и добавочный минимум линии
и добавочный минимум линии 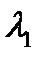 совпадает, следовательно:
совпадает, следовательно: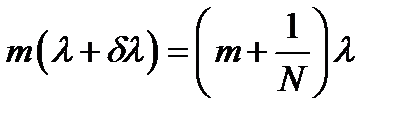 (27)
(27)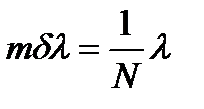 (28)
(28)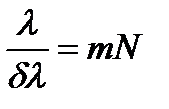 (29)
(29)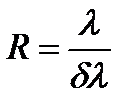 (30)
(30) В результате получим:
В результате получим: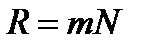 (31)
(31)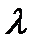 больше минимально возможной абсолютной погрешности
больше минимально возможной абсолютной погрешности 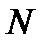 в формуле для разрешающей силы – это число щелей, принимающих участие в образовании главного максимума порядка
в формуле для разрешающей силы – это число щелей, принимающих участие в образовании главного максимума порядка 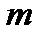 . Если поперечный размер падающего на решетку пучка света
. Если поперечный размер падающего на решетку пучка света 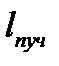 больше длины решетки
больше длины решетки 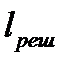 , то
, то 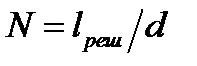 , где
, где 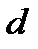 – постоянная решетки.
– постоянная решетки.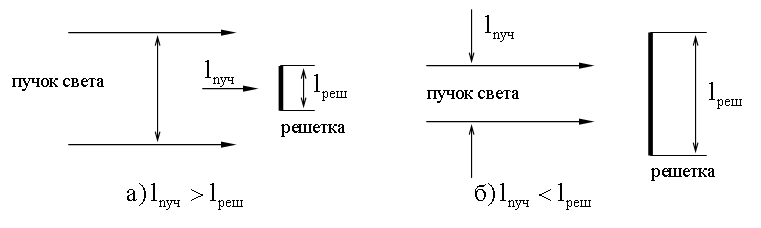
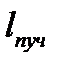 <
< 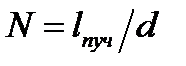
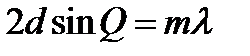 ,
, 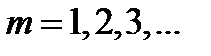 , (32)
, (32)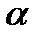 , под которыми наблюдаются главные максимумы, выполняются с помощью гониометра.
, под которыми наблюдаются главные максимумы, выполняются с помощью гониометра.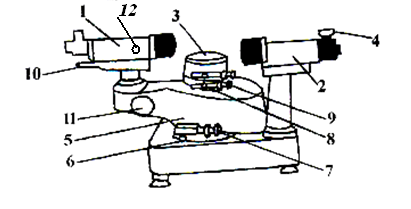
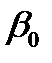 .
.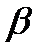 для линий ртути в спектрах 1-го и 2-го порядков. Затем поверните зрительную трубу влево и снимите отчеты
для линий ртути в спектрах 1-го и 2-го порядков. Затем поверните зрительную трубу влево и снимите отчеты 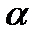 , под которыми наблюдаются главные максимумы 1-го, 2-го, (–1)-го и (–2)-го порядков. Если
, под которыми наблюдаются главные максимумы 1-го, 2-го, (–1)-го и (–2)-го порядков. Если 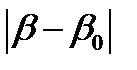 <90º, то
<90º, то 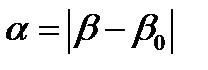 . Если
. Если 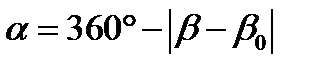 .
.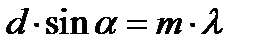 ,
, 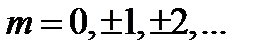 (1)
(1)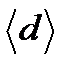 . Вычислите погрешность по формуле для погрешностей прямых измерений.
. Вычислите погрешность по формуле для погрешностей прямых измерений.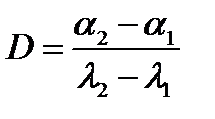 , (2)
, (2)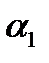 и
и 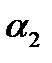 – углы дифракции для желтого дублета ртути;
– углы дифракции для желтого дублета ртути; 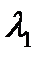 и
и 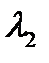 – длины волн этого дублета.
– длины волн этого дублета.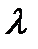 , нм
, нм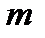 =1
=1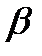
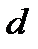 , мкм
, мкм
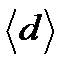 , мкм
, мкм
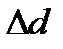 , мкм
, мкм
 , заменяющей реальный источник света, выбрать сферу с центром в точке, где расположен источник. В некоторый момент времени сфера является волновым фронтом, поэтому в дальнейшем будем называть ее волновым фронтом.
, заменяющей реальный источник света, выбрать сферу с центром в точке, где расположен источник. В некоторый момент времени сфера является волновым фронтом, поэтому в дальнейшем будем называть ее волновым фронтом.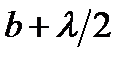 ,
,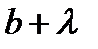 , (1)
, (1)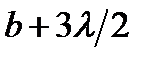 ,
,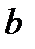 – расстояние от P до волнового фронта,
– расстояние от P до волнового фронта, 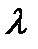 – длина световой волны, которую излучает источник (при этом предпола
– длина световой волны, которую излучает источник (при этом предпола 


